Математические основы включают анализ методов временных рядов (ARIMA, SARIMA), машинного обучения (LightGBM, LSTM) и их адаптацию к задаче прогнозирования пассажиропотока. Предложена гибридная модель, сочетающая градиентный бустинг (ансамблевый метод машинного обучения) для статических признаков и LSTM для временных зависимостей. Формализована задача как многомерная регрессия с использованием 42 признаков, включая лаговые переменные, погодные условия и календарные метки.
Модель ARIMA (AutoRegressive Integrated Moving Average) объединяет принципы AR и MA и вводит компоненту интегрирования (разности), позволяющую моделировать нестационарные ряды:

Для учёта периодичности (например, суточных или недельных циклов) используется расширение ARIMA — модель SARIMA(p,d,q)(P,D,Q,s):

SARIMA позволяет учитывать закономерности типа “вечерние часы — повышенная загруженность” или “выходные — пониженный поток”.
Обучение модели происходит на исторических данных о пассажиропотоке, агрегированных в 15-минутные интервалы, с использованием алгоритма градиентного бустинга LightGBM, который оптимизирует функцию потерь MSE путем последовательного построения ансамбля решающих деревьев. В процессе обучения модель автоматически выявляет нелинейные зависимости между признаками (лаги, время суток, погода) и целевой переменной, минимизируя среднеквадратичную ошибку прогноза на валидационной выборке.
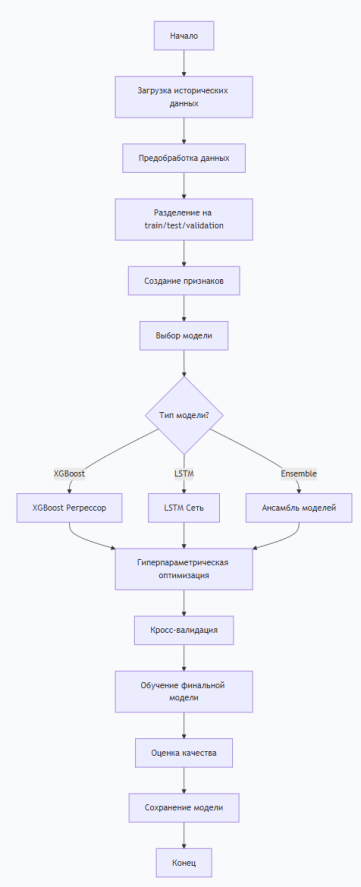
Рис. 1. Схема процесса обучения модели
Проблема загруженности и её последствия
Загруженность общественного транспорта проявляется несколькими признаками: высокая плотность пассажиров в салоне, длительные стоянки на остановках, превышение вместимости транспортных единиц, сдвиги в расписании и увеличение интервалов из-за задержек.
Последствия перегрузок включают:
— ухудшение качества обслуживания пассажиров (неудобство, переполненность);
— рост времени в пути и снижение надёжности расписания;
— дополнительный износ подвижного состава и инфраструктуры;
— экономические убытки для операторов и муниципалитетов;
— снижение привлекательности общественного транспорта по сравнению с личным автомобилем.
Необходимость прогнозирования загруженности
Прогнозирование загруженности позволяет:
— планировать интервалы движения и оптимизировать расписание;
— динамически перераспределять подвижной состав в ответ на ожидаемые пики спроса;
— информировать пассажиров о загруженности и предлагать альтернативы;
— поддерживать принятие решений на уровне городского управления транспортом.

Рис. 2. Диаграмма последовательности для прогнозирования
Литература:
1. Андреев А. Ю. Анализ данных и машинное обучение. — М.: Бином, 2020.
2. Астафьев А. Нейронные сети и глубокое обучение. — СПб.: Питер, 2019.
3. Боев Н. Ю. Моделирование пассажиропотоков городского транспорта. — М.: Транспорт, 2021.
4. Батыршин И. З. Искусственный интеллект: модели и методы. — Казань: КФУ, 2018.

