Моделирование плотности транспортных потоков



Все возрастающая интенсивность транспортных потоков в городах, делает актуальным применение математических методов, позволяющих осуществлять их автоматическое управление на основе использования методов современной теории управления. Это позволяет обоснованно давать рекомендации по управлению автомобильными потоками с целью предотвращения аварийных ситуаций и снижения вероятности возникновения транспортных заторов.

Система управления транспортными потоками является классическим примером сложной системы с присущими ей свойствами: наличием цели управления; большими размерами по числу выполняемых функций; сложным, вероятностным и динамическим поведением; необходимостью высокой автоматизации управления.

Целью данной работы является построение модели плотностей транспортных потоков. Для этого по экспериментальным данным была проведена регистрация плотности транспортных потоков на двух разных перекрестках. На рис. 1 по оси абсцисс откладывается число транспортных средств, проехавших мимо наблюдателя в течении 5 секунд, по оси ординат — дискретное время с шагом дискретизации также 5 секунд.

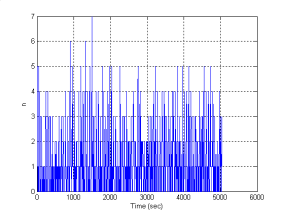
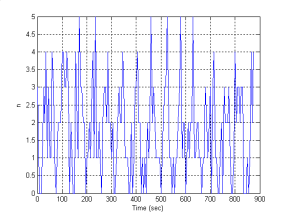
а)б)

Рис. 1. Плотности транспортных потоков

Оценка математического ожидания транспортных потоков рассчитывается по формуле (1)

.(1)

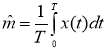
Соответственно оценки математических ожиданий для потоков равны: для первого потока m = 1,78 машин, для второго потока m = 2,172 машин.

Оценка дисперсии

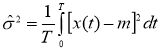
Соответственно равны: для первого потока σ = 1,7588σ =4,52, а для второго потока σ = 1,7588.

Оценка корреляционной функции определяется по формуле:

,

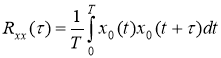
где — центрированный случайный сигнал.

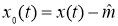
На рисунках 2 показаны рассчитанные по временным трендам автокорреляционные функции.

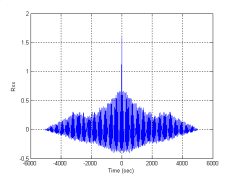
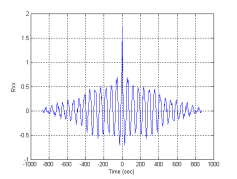
а)б)

Рис. 2. Автокорреляционные функции транспортного потока

Для получения приемлемой точности оценок характеристик случайных процессов длительность реализации процесса по которой вычисляются оценки должна превышать интервал корреляции. Интервал корреляции — это значение аргумента корреляционной функции начиная с которого все ее последующие значения не превышают . Спектральные плотности мощности транспортных потоков показаны на рисунке 3.

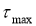
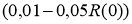
а)б)

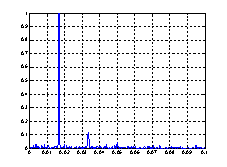
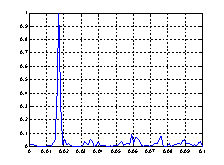
Рис. 3. Спектральные плотности мощности транспортного потока

На рисунках 4 показаны гистограммы распределения транспортных потоков.

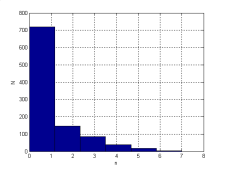
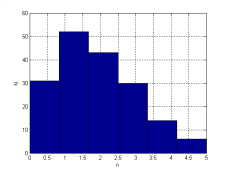
а)б)

Рис. 4. Гистограммы распределения транспортных потоков

Анализ полученных результатов позволил установить периодичность транспортного потока, обусловленную работой светофоров.

Проверим статистическую гипотезу по критерию Колмогорова-Смирнова (также известный, как критерий согласия Колмогорова) о принадлежности эмпирического распределения, заданного гистограммами (рисунок 4), распределению Пуассона.

Критерий Колмогорова-Смирнова о проверке гипотезы об однородности двух эмпирических законов распределения является одним из основных непараметрических методов, так как достаточно чувствителен к различиям в исследуемых выборках. Данная гипотеза подтвердилась, следовательно, интенсивность транспортных потоков распределена по закону Пуассона. Модели транспортных потоков, построенные по экспериментальным данным показаны на рисунке 5.

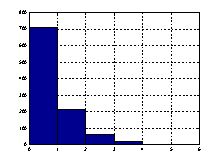
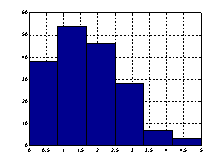
а)б)

Рис. 5. Гистограммы распределения моделей транспортных потоков

На рисунках 6 показаны рассчитанные по временным трендам автокорреляционные функции.

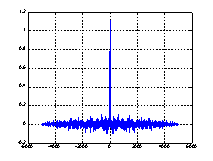
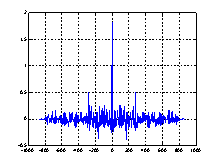
а)б)

Рис. 6. Автокорреляционные функции моделей транспортных потоков

Спектральные плотности мощности моделей транспортных потоков показаны на рисунке 7.

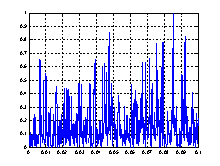
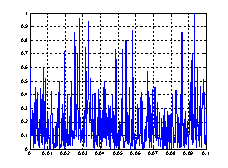
а)б)

Рис. 7. Спектральные плотности мощности моделей транспортного потока

На рисунке 8 показаны модели плотностей транспортных потоков.

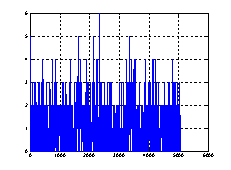
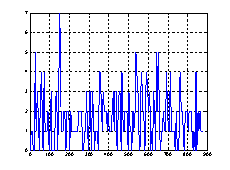
а)б)

Рис. 8. Модели плотностей транспортных потоков

Спектральные плотности мощности моделей транспортного потока заметно отличаются от спектральной плотности мощности потока, снятого экспериментально. На рисунке 3 просматривается периодическая составляющая, обусловленная работой светофоров. Этот период равен циклу управления на ближайшем светофоре и равен 60 секунд. В приведенной модели данная составляющая отсутствует. По рисункам видно, что модели распределения Пуассона мало отличаются от экспериментальных данных.

Литература:

1. Автоматические системы транспортных средств / В. В. Беляков и др. — М.: Форум, 2016. — 352 с.
2. Бершадский, В. Ф. Основы управления механическими транспортными средствами и безопасность движения / В. Ф. Бершадский, В. И. Дудко, Н. И. Дудко. — М.: Амалфея, 2016 . — 458 с.
3. Случайные процессы. Примеры и задачи Т.1.Случайные величины и процессы: Учебное пособие для вузов. − Москва: “Радио и связь”, 2003.
4. Жанказиев С. В. Интеллектуальные транспортные системы: учеб. пособие / С. В. Жанказиев. — М.: МАДИ, 2016–120 с.