Эконометрическая модель оценки коммерческого риска как ресурса

В статье рассматривается этапы построения эконометрической модели оценки коммерческого риска как ресурса. Приводится обоснование основных идей применения концепции «риск-ресурс» в анализе коммерческого риска.

Ключевые слова и фразы: коммерческий риск, риск как ресурс, модель коммерческого риска, анализ и оценка коммерческого риска, эконометрическая модель оценки.

Ресурсной подход [1] в определении коммерческого риска под которым мы понимаем не только величину возможных потерь коммерческой деятельности предприятий, но и величину прибыли, которую они своевременно не смогли получить, предполагает построение модели его оценки на основе применения базовых идей концепции «риск-ресурс» [2].

Разработка новой модели оценки, в которой будут учтены действующие на рынке тренды и динамика экономической конъюнктуры расширит диапазон возможностей предприятия в принятии управленческих решений.

Отметим, что при достижении рыночного равновесия величину коммерческого риска косвенно характеризуют такие показатели как: разность между величинами (объемами) спроса и предложения; соотношение показателей их эластичности; отклонение цен спроса и предложения от равновесной цены, а также объемов спроса и предложения от равновесного объема; соотношение излишков продавцов и покупателей и т. д.

В качестве показателя оценки коммерческого риска в предлагаемой модели будем использовать величину расхождения между рыночным предложением и спросом, которую можно рассчитать следующим образом:

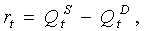                                                                                                   (1)

где 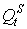 — объем производства (предложение) в момент времени t;  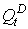— объем спроса (величина потребления) в момент времени t.

Предлагаемый показатель оценки коммерческого риска может быть однозначно оценен в долгосрочном периоде времени, поскольку в реальности не происходит одномоментной корректировки объема предложения (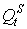) или спроса (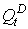). Постепенная их корректировка при достижении нового состояния рыночного равновесия, позволяет не только выявлять ситуацию коммерческого риска, но и исследовать вопрос о существовании соотношения между величиной риска и показателем, характеризующим диспропорцию рыночного предложения и спроса (r_t). Практическое применение данного показателя позволяет расширить возможности моделирования коммерческих рисков и оценить их величину показателем, представляющим собой математическое ожидание случайной величины рассчитанной на основе усредненных оценок возможных отклонений разности между объемами предложения и спроса от тренда.

Реализация данного рассмотренного подхода связана с построением эконометрической модели, в которой в отличие от чисто математической будут максимально применены основные положения концепции «риск-ресурс». Это обеспечит полное и обоснованное представление об оценке коммерческого риска на основе проявляющихся колебаний при достижении равновесия на рынке [3].

На формальном уровне проведенные теоретические обоснования оценки коммерческого риска могут быть идентифицированы с помощью следующей модели:

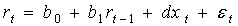                                                                           (2)

где r_t — величина расхождения между предложением и спросом на рынке в момент времени t; b₀, b₁ — оцениваемые параметры той части модели, которая отвечает за тренд уровня рассматриваемой величины; d — оцениваемый параметр стохастической составляющей модели, характеризующий средний уровень возможного отклонения фактически наблюдаемого расхождения от тренда и интерпретируемый как величина риска; х_t — ненаблюдаемая дискретная независимая переменная принимающая случайным образом два значения: 1 или -1; ε_t — ненаблюдаемая случайная величина, характеризующая ту часть вариации моделируемой переменной, которая не объясняется включенными в модель регрессорами.

Предпочтительность этой модели, объясняется двумя фактами. Во-первых, ее построение осуществляется с помощью хорошо известного метода наименьших квадратов. Во-вторых, модели данного типа сохраняют свою корректность на любом промежутке времени, что позволят их использовать как для анализа, так и для прогнозных расчетов.

Непрерывно составляющая модели (2) представляет собой авторегрессионную модель 1-го порядка, которая обеспечивает более высокий уровень адекватности отражение динамики, чем представление той же самой динамики в виде элементарной функции от времени. А оцениваемый параметр d модели (2) характеризует среднюю величину колебания вокруг тренда и выступает в роли измерителя средней величины коммерческого риска.

Такой подход к оценке коммерческого риска предлагается впервые и требует определенных пояснений. Его отличие от общепринятого заключается в том, что в модели (2) с помощью d оценивается средняя величина колебаний не относительно среднего значения, а вокруг тренда. Данное отличие не является принципиальным, так как можно построить модель (2) без тренда, и тогда d будет измерителем колебаний вокруг среднего. Но есть более существенное отличие, дающее ряд преимуществ перед традиционным измерением с помощью σ:

-                    измерение риска с помощью коэффициента регрессии, которым является d, позволяет одновременно по методу наименьших квадратов с его оценкой рассчитать и характеристики статистической надежности.

-                    риск, измеренный по d можно тестировать на предмет воспроизведения отклонений исторического периода.

Модель (2) имеет вид обычной регрессионной, однако ее построение осуществляется в несколько этапов. Это обуславливается тем, что модель содержит как наблюдаемые, так и ненаблюдаемые переменные, а при определении и идентификации отдельных элементов модели необходимо обеспечить корректную замену ненаблюдаемых значений наблюдаемыми.

При построении предлагаемой модели будем использовать гипотезу альтернативных ожиданий, суть которой сводится к тому, что ожидаемый результат носит альтернативный характер, т. е. одни и те же ресурсы могут привести как к положительным, так и к отрицательным результатам. Кроме того, результаты реализации альтернативного события можно будет сравнить с некоторым пороговым значением.

Данная гипотеза позволяет провести идентификацию дискретной независимой ненаблюдаемой переменной х_t на историческом периоде времени [3].

Для этого в начале строим усеченный вариант модели (2) –регрессионное уравнение непрерывной составляющей:

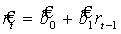                                         .                                                               (3)

Параметры 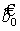,  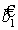будут оценены на основе метода наименьших квадратов (пакет анализа Excel). Возможность дальнейшего применения данного уравнений определяется его стабильностью, которая обеспечивается условием .

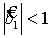Далее формируются значения дискретной независимой переменной х_t в соответствии со следующим правилом: на историческом периоде ненаблюдаемой переменной присваивается значение равное +1, если фактическое значение моделируемого показателя выше заранее заданного порогового значения, и присваивается значение равное -1, если фактическое значение меньше этого порогового значения.

В качестве индикатора (порогового значения), на основе которого формируются значения ненаблюдаемой переменной х_t на историческом периоде используем отклонение 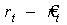, которое представляет собой реакцию рынка на проявляющуюся динамику и изменения в момент времени t.

Тогда ненаблюдаемая дискретная независимая переменная х_t идентифицируется в соответствии с выражением:

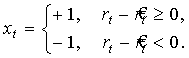                                                                                        (4)

Сформированная таким образом дискретная переменная х_t дает возможность на основе метода наименьших квадратов (пакет анализа Excel) оценить все коэффициенты регрессионной модели (2):

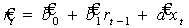                                                                                        (5)

Если данная модель обеспечивает достаточно высокую точность, то ее можно использовать как для анализ Выбор планового ориентира и его обоснование в трекинг-анализе коммерческих рисков а, так и прогноза. При чем варьирование значений независимой переменная х_t, обеспечивает альтернативность прогнозных расчетов и позволяет рассматривать коммерческий риск не только с позиции ущерба (потерь), но и со стороны прибыли, т. е. в соответствии с концепцией «риск-ресурс»:

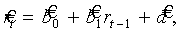                                                                                          (6)

или

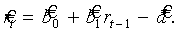                                                                                          (7)

Для логической завершенности предлагаемой эконометрической модели, с помощью которой рассчитываются альтернативные прогнозные варианты, необходимо предусмотреть возможность определения вероятностей, оценивающих реальность прогнозных вариантов.

Реализация этой задачи связанна с построением вероятностного распределения, которое позволит связать экспертно-аналитические оценки с прогнозной моделью.

Так как, в нашем случае в исходное уравнение (2) была включена только одна дискретная переменная х_t, то вероятность реальности отдельных вариант будут оценены на основе модели бинарного выбора.

Предположим, что вероятность возможной реализации конкретного варианта описывается логит-моделью:

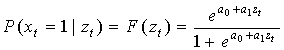                                                                (8)

где a₀, a₁ — параметры модели бинарного выбора, оцениваемые с помощью метода максимального правдоподобия; z_t — независимая переменная, от которой зависит вероятность реальности вариантов формируемого прогнозного образа..

В ходе построения логит-модели необходимо наличие данных зависимой и независимой переменных.

В качестве дискретной зависимой переменной будем использовать значения дискретной ненаблюдаемой переменной х_t, заменив отрицательное значение нулевым:

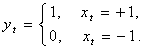                                                                                                   (9)

Значения независимой переменной логит-модели (8) 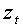 определяются на основе экспертно-аналитической шкалы при частичной ее рандомизации. В прогнозных расчетах построение такой шкалы носит обязательный характер.

В предлагаемой модели для построения специальной экспертно-аналитической шкалы будем использовать следующее отклонение:

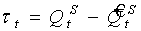                                                                                                    (10)

где 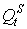 — величина предложения в момент времени t;  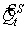— трендовое значение предложения в момент времени t.

Отметим, что наш выбор является не случайным и объясняется тем, что состояние на рынке характеризуется объемами спроса и предложения, уровнем цен и инфляцией, а данные показатели за исключением величины предложения практически не управляемы. Кроме этого, полученные оценки коммерческого риска должны быть использованы в принятии управленческих решений, а производители могут регулировать только величину предложения.

Процедура построения шкалы достаточно проста. Сначала строим авторегрессионное уравнение 1-го порядка для функции предложения:

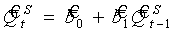                                         .                                                 (11)

Затем рассчитываем отклонения 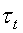 (10) и нормируем их :

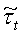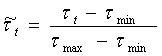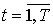                                        ,                                        (12)

Полученная последовательность подвергается частичной рандомизации:

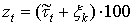                                         ,                                                            (13)

где 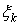– равномерно распределенная случайна я величина с небольшим диапазоном возможных значений.

Частичная рандомизация, с одной стороны, необходима для того, чтобы избежать случаев неразрешимости системы, получаемой в результате дифференцирования функции максимального правдоподобия. А с другой, — она вносит в оценку рациональной составляющей элемент случайности, который хотя и в незначительной степени, но все же искажает эту составляющую.

На основе определенных выше указанным способом значений зависимой и независимой переменных и итерационной схемы обобщенного метода наименьших квадратов, реализованной в пакете STATISTICA, проводиться оценка параметров логит-модели a₀, a₁ [4].

С учетом идентификации ненаблюдаемой дискретной независимой переменной х_t третья составляющая модели (5) будет представлена виде вероятностного распределения, а саму модель можно записать как условное математическое ожидание, следующим образом:

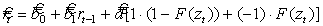                                                                                                      (14)

или

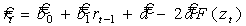                                                                          (15)

В модели (15) уже нет ненаблюдаемой переменной x_t, поэтому ее без проблем можно использовать в расчетах прогнозного профиля величины коммерческого риска.

Таким образом, в окончательном виде оцененная эконометрическая модель, предназначенная для прогнозных расчетов величины коммерческого риска, записывается в виде нелинейного регрессионного уравнения:

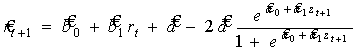                                              (16)

Модель (16) предназначена для проведения прогнозных расчетов и поэтому наделена специфическими свойствами, которые необходимы для того, чтобы обеспечить соблюдение корректности при получении прогнозных оценок коммерческих рисков.

В рассматриваемом случае, когда риск возникает из-за неопределенности, которая имеет место при выборе одного из двух возможных вариантов, усредненная величина коммерческого риска рассчитывается по формуле:

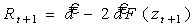                                                                                      (17)

С помощью выражения (17) определяется диапазон возможных значений моделируемого показателя напрямую зависящего от состояния на рынке. Однако природа данного показателя в значительной степени субъективна, что затрудняет его практическое использование без предварительного построения шкалы оценки риска и исследования ее чувствительности к экспертным оценкам.

Модель легко обобщается на случай, когда число вариантов описывающих прогнозный образ больше двух. Для этого дополнительно вводят дискретные переменные. При этом количество вариант возрастает в геометрической прогрессии, а оценка этих вариантов проводится с помощью мультиноминальной логит-модели множественного выбора. Наращивание вариантов, по сути, приводит к ситуации, когда дискретный прогнозный образ превращается в непрерывный, накрывающий все многообразие будущего.

Рассмотренная модель с определенной долей вероятности позволяет получать как положительные, так и отрицательные значения оценки коммерческих рисков, тем самым рассматривать его как реальный ресурс предприятия. В ресурсной интерпретации анализа коммерческого риска могут возникнуть следующие ситуации:

1.         Если 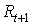<0, то диспропорция между объемом спроса и предложения характеризуется избытком производства, а величина показывает возможный размер убытков, которые буде нести производитель за счет сокращения цены и сворачивания производственных мощностей.

2.         Если 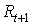>0, то диспропорция между объемом спроса и предложения характеризуется дефицитом товаров, возникает риск недополучения прибыли. Положительное значение оценки риска свидетельствует о возможности наращивания объемов производства, производственного потенциала или более полное использование производственных мощностей.

3.         Если 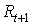=0, то диспропорция между объемом спроса и предложения отсутствует, что характерно для рыночного равновесия.

Предлагаемая модель оценки риска позволит изменить отношение к восприятию коммерческого риска и рассматривать его как своеобразный ресурс.

Литература:

1.      Бублик, Н. Д. Риск-ресурс: проблемы венчурно-стохастической деятельности [текст] / Н. Д. Бублик, В. Б. Силантьев. — Уфа: БТИПБ, 1999. — 376с.

2.      Грачева, М. В. Риск-менеджмент инвестиционного проекта: учебник для студентов вузов, обучающихся по экономическим специальностям [текст] / под ред. М. В. Грачевой. — М.: ЮНИТИ — ДАНА, 2009. — 544 с.

3.      Давнис, В. В. Прогнозные модели экспертных предпочтений: монография [текст] / В. В. Давние, В. И. Тинякова. — Воронеж: Изд-во Воронеж. гос. ун-та, 2005. — 248 с.

4.      Давнис, В. В. Адаптивные модели: анализ и прогноз в экономических системах [текст] / В. В. Давние, В. И. Тинякова. — Воронеж: Изд-во Воронеж. гос. ун-та, 2006. — 380 с.