Построение эконометрических моделей для анализа эффективности инвестиций в основной капитал (региональный аспект)

Салов, Владимир Олегович

В статье описывается поэтапное построение регрессионной модели динамики инвестиций в основной капитал классифицированных по источникам финансирования. Выполнена детальная оценка значимости полученной регрессионной моделей, а также дана характеристика полученных результатов с точки зрения эффективности и инвестиционной отдачи в рамках регионального аспекта.

Ключевые слова: инвестиции в основной капитал, эффективность инвестиционной деятельности, регрессионный анализ, валовый региональный продукт.

Анализ инвестиционной среды, источников инвестиционных ресурсов, способов освоения, а также анализ показателей эффективности инвестиционной деятельности и особенно обновление основного капитала хозяйствующих субъектов, на современном этапе развития экономики России, приобретает наиважнейшее значение.

Динамика инвестиционных процессов, направленных на основной капитал, является определяющей в характеристике воспроизводственных возможностей производственных секторов экономики. Ввиду этого исследование специфики инвестиционных процессов и их результатов, является ключевой задачей экономической статистики.

В условиях современной экономики поиск оптимальных источников финансирования капиталовложений, особенно актуален. Учитывая этот факт, статистическое исследование инвестиционных процессов в основной капитал на региональном уровне, усовершенствование методологии статистической оценки и анализ инвестиций является актуальным, и имеют высокое практическое и научное значение.

Целью данного исследования является оценка и анализ инвестиций в основной капитал ключевых регионов, входящих в состав Российской Федерации.

Объектом исследования является экономика макрорегионов Российской Федерации, как совокупность экономических единиц, концентрирующих инвестиционную деятельность.

Предметом данного исследования является количественная характеристика инвестиционных процессов в основной капитал агрегированная по источникам финансирования.

Теоретической и методологической базой исследования послужили статистические данные Федеральной служба государственной статистики, аналитические исследования зарубежных и отечественных экономистов, а также материалы научных статей и периодических изданий по изучаемому вопросу.

Для обработки исходных данных были задействованы пакеты прикладных программ Microsoft Excel, Statistica и VSTAT.

Краткая характеристика аналитической части

Отношение финансового результата, выраженного через прирост валового регионального продукта (ВРП) к инвестициям в основной капитал, позволяет оценить общую эффективность инвестиционной деятельности, как отдельного региона, так и страны в целом.

Уровень эффективности инвестиционных процессов является интегральной характеристикой и зависит от множества определяющих факторов.

Для решения такого рода задачи, в данном исследовании применен инструментарий, базирующийся на использовании линейной модели многофакторной регрессии. Зависимойпеременной предполагается использовать прирост ВРП за период с 2010 по 2011 года, к общему объему инвестиций в основной капитал. Общая функциональная зависимость строиться в соответствии с многофакторной моделью типа [2, с.187]:

Y = f (x1, …, x12, e)

Анализ собранной аналитической базы будет выполнен с помощью корреляционного и регрессионного анализа. Пределы изменения коэффициентов корреляции вирируются в пределах от -1.00 до +1.00. Пороговые значения означают полностью отрицательную или полностью положительную.Отсутствие корреляции выражается значением показателя равным 0.00 [2, с.170].

Базовое предназначение множественной регрессии заключается в анализе связей между зависимой переменной и ряда независимых переменных. Данные о наличии таких связей могут быть использованы для формирования регрессионного уравнения (системы уравнений).

Исходные данные [4]

Таблица 1

Исходные данные: распределение инвестиций в основной капитал по источникам финансирования

		Прирос ВРП (реальный)	Собственные средства	Привлеченные средства
		Прирос ВРП (реальный)	Собственные средства	кредиты банков	бюджетные средства	Прочие
		(млн.руб.)	млн.руб.	млн.руб.	млн.руб.	млн.руб.
ID	Регион	Y (dY=2011–2010)	Z1	Z2	Z3	Z4
1	Белгородская обл.	116 105	36 406,3	28 893,9	18 492,1	12 520,7
2	Воронежская обл.	102 910	33 333,3	17 724,9	54 497,3	26 719,6
3	Ивановская обл.	18 908	5 872,4	2 606,6	5 572,7	15 909,3
4	Владимирская обл.	35 087	19 434,1	4 908,6	8 364,7	17 380,5
5	Брянская обл.	34 444	12 638,7	6 844,2	13 142,6	9 363,5
6	Липецкая обл.	41 006	58 724,8	9 956,8	20 726,4	12 192,0
7	Костромская обл.	14 860	7 746,3	1 359,0	2 370,7	3 624,0
8	Калужская обл.	47 462	28 156,8	17 355,9	9 683,6	19 292,7
9	Курская обл.	41 960	10 647,5	10 140,5	6 729,6	18 575,5
10	Тамбовская обл.	39 561	14 116,3	9 017,2	11 110,5	19 430,0
11	Тверская обл.	37 877	16 441,0	11 236,0	12 557,9	42 383,0
12	Тульская обл.	38 389	29 111,1	7 438,7	13 518,4	21 457,8
13	Ярославская обл.	48 504	30 362,2	5 060,4	15 253,4	21 615,0
14	Московская обл.	429 671	185 325,7	28 602,1	47 017,1	130 864,2
15	Орловская обл.	25 815	8 849,3	3 397,1	3 837,5	4 886,0
16	Рязанская обл.	33 697	19 782,9	6 133,9	9 383,7	5 321,5
17	Смоленская обл.	30 498	10 303,8	3 906,6	5 811,1	28 811,5
18	Республика Коми	83 598	35 041,7	9 771,2	5 503,3	61 996,8
19	Республика Карелия	23 961	8 936,8	2 872,5	6 793,8	4 194,8
20	Архангельская обл.	72 205	50 241,7	5 383,0	18 043,2	26 018,0
21	Ленинградская обл.	80 524	44 339,4	21 751,4	33 463,7	179 309,6
22	г.Москва	1 746 984	299 699,2	47 629,5	228 621,4	156 810,9
23	Псковская обл.	16 373	6 461,0	517,5	3 455,9	6 260,6
24	Мурманская обл.	30 744	13 436,6	2 818,6	6 602,5	15 753,3
25	Новгородская обл.	23 305	9 271,7	5 444,7	4 576,7	20 161,0
26	Вологодская обл.	57 524	25 302,0	7 405,5	8 022,6	27 839,0
27	Калининградская обл.	37 100	23 133,1	4 302,5	11 175,4	17 266,0
28	г.Санкт-Петербург	390 618	115 241,1	69 465,9	138 530,3	78 299,7
29	Республика Адыгея	8 673	2 751,1	1 656,2	3 873,9	5 754,8
30	Республика Калмыкия	4 695	2 864,7	209,1	2 878,6	1 017,6
31	Краснодарский край	213 900	184 312,1	45 644,7	102 845,0	244 979,1
32	Астраханская обл.	27 571	11 553,6	2 873,4	7 423,0	38 013,0
33	Волгоградская обл.	71 868	42 431,2	5 254,9	13 647,0	17 098,0
34	Ростовская обл.	111 717	55 154,5	21 079,2	44 535,7	37 720,6
35	Республика Башкортостан	199 253	78 256,1	9 188,6	33 844,6	31 853,7
36	Республика Марий Эл	15 293	6 334,3	4 728,4	4 572,3	6 668,9
37	Республика Мордовия	22 720	9 868,3	10 887,7	13 660,6	6 361,4
38	Республика Татарстан	281 588	128 617,1	60 525,7	67 104,6	72 696,6
39	Удмуртская Республика	63 791	29 512,4	5 984,3	9 513,5	6 137,8
40	Чувашская Республика	32 576	19 516,3	2 855,0	11 547,9	8 692,8
41	Пермский край	184 409	76 110,3	6 703,3	22 344,3	34 494,0
42	Кировская обл.	32 166	12 922,8	4 284,6	8 707,4	8 638,3
43	Нижегородская обл.	126 109	85 856,2	25 353,5	33 228,5	47 633,9
44	Оренбургская обл.	100 875	57 421,0	9 224,7	9 742,9	27 259,4
45	Пензенская обл.	30 312	14 845,4	7 765,3	13 475,0	9 592,4
46	Самарская обл.	145 336	96 603,3	10 715,4	20 276,8	37 256,6
47	Саратовская обл.	56 947	35 618,2	10 005,1	13 366,8	21 050,8
48	Ульяновская обл.	46 730	17 949,4	4 751,3	6 815,0	18 477,3
49	Курганская обл.	20 598	8 925,0	5 089,0	6 981,4	4 577,6
50	Свердловская обл.	230 967	131 322,4	27 170,1	55 405,8	52 475,7
51	Тюменская обл.	821 818	578 380,8	41 987,7	98 671,1	330 653,3
52	Челябинская обл.	131 264	80 245,3	28 864,1	24 179,4	17 832,3
53	Республика Алтай	4 368	752,2	561,8	6 646,4	1 561,6
54	Республика Бурятия	23 059	10 607,8	436,4	11 279,2	11 245,6
55	Республика Тыва	3 564	911,7	622,3	4 073,9	1 628,1
56	Республика Хакасия	20 732	5 438,8	950,7	3 161,6	12 557,9
57	Алтайский край	38 454	23 087,3	5 075,9	13 535,8	12 880,9
58	Забайкальский край	43 028	9 458,1	224,1	16 047,4	19 095,5
59	Красноярский край	150 280	155 875,4	9 875,7	41 371,1	59 787,8
60	Иркутская обл.	89 791	69 846,1	12 655,9	10 984,3	25 908,7
61	Кемеровская обл.	122 859	100 858,6	13 074,3	20 700,9	21 012,2
62	Новосибирская обл.	98 638	58 880,6	10 077,6	27 968,3	16 305,4
63	Омская обл.	71 217	37 476,4	9 808,3	11 272,2	14 639,2
64	Томская обл.	56 654	35 772,7	3 957,5	9 389,4	28 478,5
65	Республика Саха (Якутия)	99 700	60 418,3	4 175,8	30 535,4	35 363,6
66	Камчатский край	11 486	4 696,6	1 565,5	8 577,7	17 775,2
67	Приморский край	82 520	29 357,5	9 369,4	92 653,0	76 829,1
68	Хабаровский край	53 384	40 987,0	5 162,5	19 554,9	90 734,6
69	Амурская обл.	46 586	19 462,9	1 677,8	10 486,5	52 264,7
70	Магаданская обл.	16 029	5 916,8	201,7	5 916,8	4 773,8
71	Сахалинская обл.	114 372	59 406,2	21 872,3	9 316,0	44 419,6
72	Еврейская автономная обл.	5 430	714,8	75,2	5 022,5	12 998,4
73	Чукотский автономный округ	6 358	1 864,1	5,4	433,5	3 115,9

1. Расчёт корреляционной матрицы

Таблица 2

Анализ коэффициентов корреляции

	Y2	Z1	Z2	Z3	Z4
Y2	1
Z1	0,769337861	1
Z2	0,630150249	0,657719781	1
Z3	0,871543296	0,695015482	0,779617455	1
Z4	0,619857196	0,842857224	0,634035966	0,667094	1

2. Ступенчатый отсев регрессоров

Проанализировав матрицу коэффициентов парной корреляции, можно сделать вывод, что зависимая переменная Y2, т. е. «прирос ВРП» имеет максимальную связь с Z3 (бюджетные ср-ва). Коэффициент корреляции равен 0,8715. Следует подчеркнуть, что все значения независимых переменных имеют довольно высокую связь с зависимой, это говорит о том факте, что в реальных условиях, каждая из (Z1, Z1, Z3, Z4) имеет большое влияние на зависимую переменную (т. е. динамика прироста ВРП довольно сильно зависит от изменение каждого из анализируемых факторов). Ввиду этого, при дальнейшем анализе и построении уравнения множественной регрессии следует это учитывать.

Наряду с этим, также можно наблюдать и проявление мультиколлинеарности между независимыми коэффициентами. Так, например, между Z1 и Z4 сильнее всего проявляется данный эффект (0,842857224). В тоже время, коэффициенты Z2 и Z3, довольно влияют друг на друга.

Для того, чтобы избавиться от мультиколлинеарности обычно исключают одну из переменных мультиколлинеарной пары. Как правило удаляют ту переменную, у которой больше значение F-критерия т. к. оно больше влияет на общую мультиколлинеарность модели, а также проводят тест на наличие мультиколлинеарности каждой пары переменных, определяя статистическую значимость каждого из параметров.

Воспользовавшись t-критерием Стьюдента, определим значимость коэффициентов корреляции. Сравним табличное значение с расчетным. Ттабл 1,995468907, при степени свободы 68 73–4-1.

Таблица 3

Анализ значимости коэффициентов корреляции

	Коэфф-ы	Станд-я ошибка	t-статистика
Y-пересечение	-16351,55892	13800,18896	-1,184879349
Z1	1,579612122	0,259355674	6,090524633
Z2	-3,509474986	1,274218991	-2,754216512
Z3	5,352883298	0,526315749	10,17047904
Z4	-1,143610416	0,37403996	-3,057455184

Сравнив табличное значение критерия Стьюдента с расчетными (используя стандартный инструмент анализа данных «регрессии», четко видно (подтверждая предыдущее предположение), что статистически значимыми являются только Z1 и Z3, поскольку Z2 и Z4 меньше табличного значения).

Ввиду того, что в двух парах мультиколлинеарных факторов довольно сложно выделить явно лишний (даже используя методику анализа Фаррара-Глоубера и оценку критерия Стьюдента), считаю целесообразным выбрать два направления развития аналитической части:

Для составления первого уравнения исключить (на первом этапе исключения) коэффициент Z4 (ввиду его наименьшей корреляции с Y2);
Составить отдельное уравнение множественной регрессии для фактора Z4.

Для комплексного анализа влияния переменных факторов на прирост ВРП, считаю целесообразно сделать это по следующим причинам:

а) при анализе динамики изменения % инвестирования в основной капитал, источник финансирования «Z4 — Прочие», довольно часто показывает значительные объемы по ряду регионов (например, к таким регионам, можно отнести Ленинградскую обл.).

б) С точки зрения комплексного анализа, эти данные могут быть полезны при расшифровке, на более мелкие составляющие.

Составить отдельное уравнение для Z2, опираясь на аналогичную логику, описанную в п.2б.

Поэтапное исключение факторов

1) Без учета коэффициента Z4

Таблица 4

Анализ коэффициентов корреляции

	Y2	Z1	Z2	Z3
Y2	1
Z1	0,769337861	1
Z2	0,630150249	0,657719781	1
Z3	0,871543296	0,695015482	0,779617455	1

Таблица 5

Анализ значимости коэффициентов корреляции

	Коэфф-ы	Станд-я ошибка	t-статистика
Y-пересечение	-22168,62429	14471,64956	-1,531865748
Z1	1,033685451	0,199158281	5,190271015
Z2	-3,863799622	1,343508808	-2,875901966
Z3	5,162743708	0,553341688	9,330118835
		Тст-та табл	1,99494539

Исключив параметр Z4 из анализа, получили корреляционную матрицу и провели регрессионный анализ. По представленной корелляционной матрице можем наблюдать, что по-прежнему сохраняется большая мультиколлинеарность между Z2 andZ3 (0,779617455). Это в очередной раз подтверждает, что для построения адекватного уравнения регрессии необходимо исключить данный параметр.

В тоже время, проведя сравнительную оценку табличного значения t-критерия Стьюдента, с расчетными данными, также можем наблюдать, что коэффициента t-статистика для Z2 меньше табличного значения. Следовательно, исключим параметр Z2.

3. Уравнение множественной регрессии (для значащих факторов)

1) Проведя регрессионный анализ, выведем итоги и составим уравнение регрессии:

Показатели регрессионного анализа		*Y2 -35780,5679+0,886Z1+4,215Z3*
Множественный R	0,900757042
Стандартная ошибка	100429,8038
Rквадрат	0,811363249
Нормированный Rквадрат	0,805973627
Наблюдения	73
Показатели дисперсионного анализа…
	df	SS	MS	F
Регрессия…	2	3,03677E+12	1,51839E+12	150,5417874
Остаток…	70	7,0603E+11	10086145484
Итого	72	3,7428E+12

	Коэфф-ы	Станд. ошиб.	t-стат.	P-Знач.
Y-пересечение	-35780,56792	14368,45711	-2,490216427	0,015143211
Z1	0,886291652	0,202198769	4,383269283	4,02648E-05
Z3	4,215167265	0,467066796	9,024763272	2,38157E-13

2) Анализ результатов

Оценим значимость полученной модели с помощью F- Критерия Фишера и t-критерия Стьюдента.

2.1) F- Критерия Фишера

Табличное и расчетное значение F-Критерия фишера
Табличное	3,127675601
Расчетное	150,5417874

Т. к. Fтабл <Fрасч, уравнение статистически значимо.

2.2) t-критерия Стьюдента

Табличное и расчетное значение t-критерия Стьюдента
Табличное	tтабл (0.05, 70) 1,994
Z1	4,383269283
Z3	9,024763272

Т. к. tтабл<Z1, Z3, то параметры уравнения Z1 и Z3 — статистически значимы.

2.3) Полученное значение коэффициента множественной корреляции показывает, что 90,07 % суммарной вариации объясняется вариабельностью анализируемых в модели факторов.

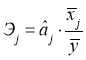
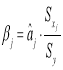
2.4) Проведем анализ коэффициента эластичности, бетта-коэффициента и дельта-коэффициента [2, с.193]:

	Y2ср	Z1cp	Z3cp
Среднее	107388,73	50102,99	23430,49
СКО	227998,63	81412,69	35244,52
К/т эластичности		0,414	0,920
бета		0,316	0,652
дельта		0,300	0,700

3) Вывод

А) Анализ коэффициентов эластичности:

Эz1 0,414, т. е. данный результат позволяет сделать нам вывод о том, что ВРП изменится на 4,14 %, при изменении фактора «собственные средства» на 1 %.

Эz3 0,920, т. е. данный результат позволяет сделать нам вывод о том, что ВРП изменится на 9,2 %, при изменении фактора «бюджетные средства» на 1 %.

В) Анализ бета-коэффициентов:

Bz1 0,316, т.е при изменении фактора «собственные средства» на 1 СКО, значение СКО исследуемой переменной изменится на 0,316.

Bz3 0,652, т.е при изменении фактора «бюджетные средства» на 1 СКО, значение СКО исследуемой переменной изменится на 0,652.

Г) Анализ дельта-коэффициентов:

∆z1 0,3 — средняя доля влияния фактора Z1. ∆z3 0,7 — средняя доля влияния фактора Z3.

Таким образом, делаем вывод, что, преобладает степень влияния фактора «бюджетные средства» над показателем «собственные средства».

Вывод:

Отсюда следует, что именно факторы «Собственные средства» и «Бюджетные средства» более других воздействуют на формирование ВРП в данной модели.

4) Весовые значения приоритетности факторных признаков

Таблица 6

Сила влияния факторных признаков

Детерминанта	Сила влияния факторного признака	Экономическая трактовка
Z1 — Инвестиции в основной капитал (собственные средства)	0,886	Наращивание объема инвестиций со стороны частных инвесторов (собственных средств) в основной капитал способствует росту ВРП. Общая эффективность вложения собственных средств, показывает, что инвестиционная отдача носит средний характер, об этом нам говорит значение коэффициента (0,886).
Z3 — Инвестиции в основной капитал (бюджетные средства)	4,215	Наращивание инвестиций приводит к довольно значительно росту ВРП и характеризуется большой инвестиционной отдачей. Приток инвестиций в объеме 1 млн, способен давать до 4,2 млн прироста ВРП.

4. Расчет параметров линейной регрессии для каждого фактора Zi

4.1) Для Z1 получены следующие данные

Показатели регрессионного анализа		Уравнение регрессии зависимости ВРП от собственных средств имеет вид: Y2 -560,8253883+2,154553139*Z1
Множественный R	0,769337861
Стандартная ошибка	146677,2802
Rквадрат	0,591880745
Нормированный Rквадрат	0,586132586
Наблюдения…	73

Показатели дисперсионного анализа
	df	SS	MS	F	Значимость F
Регрессия…	1	2,21529E+12	2,21529E+12	102,9687582	1,852E-15
Остаток…	71	1,52751E+12	21514224513
Итого	72	3,7428E+12

	Коэфф-ы	Станд. ошиб.	t-стат.	P-Знач.	Ниж 95 %
Y-пересечение	-560,8253883	20196,20477	-0,02776885	0,977924416	-40830,914
Z1	2,154553139	0,212326633	10,14735228	1,8518E-15	1,7311859

4.2) Для Z2 получены следующие данные

Показатели регрессионного анализа		Уравнение регрессии зависимости ВРП от банковских кредитов имеет вид: *Y2 -8545,4785+10,3693745Z2**
Множественный R	0,63015025
Стандартная ошибка	178277,193
Rквадрат	0,39708934
Нормированный Rквадрат	0,38859764
Наблюдения…	73

Показатели дисперсионного анализа …
	df	SS	MS	F	Значимость F
Регрессия…	1	1,4862E+12	1,48623E+12	46,762057	2,3211E-09
Остаток…	71	2,2566E+12	31782757697
Итого	72	3,7428E+12

	Коэфф-ы	Станд. ошиб.	t-стат.	P-Знач.	Ниж. 95 %
Y-пересечение	-8545,4785	26885,0997	-0,31785184	0,75153029	-62152,845
Z2	10,3693745	1,516372	6,838278802	2,3211E-09	7,3458146

4.3) Для Z3 получены следующие данные

Показатели регрессионного анализа
Множественный R	0,8715433	Уравнение регрессии зависимости ВРП от бюджетных средств имеет вид: Y2 -24713,739+5,63805824*Z3
Стандартная ошибка	112576,471
Rквадрат	0,75958772
Нормированный Rквадрат	0,75620163
Наблюдения…	73
Показатели дисперсионного анализа …
	df	SS	MS	F	Значимость F
Регрессия…	1	2,843E+12	2,84299E+12	224,326008	1,1392E-23
Остаток…	71	8,9982E+11	12673461935
Итого	72	3,7428E+12

	Коэфф-ы	Станд. ошиб.	t-стат.	P-Знач.	Ниж. 95 %
Y-пересечение	-24713,739	15855,6733	-1,55866853	0,12352147	-56329,054
Z3	5,63805824	0,37643478	14,97751676	1,1392E-23	4,88746861

4.4) Для Z4 получены следующие данные

Показатели регрессионного анализа		Уравнение регрессии зависимости ВРП от прочих источников инвестиционных ресурсов имеет вид: Y2 12730,0376+2,60309142*Z4
Множественный R	0,6198572
Стандартная ошибка	180169,41
Rквадрат	0,38422294
Нормированный Rквадрат	0,37555003
Наблюдения…	73
Показатели дисперсионного анализа …
	df	SS	MS	F	Значимость F
Регрессия…	1	1,4381E+12	1,43807E+12	44,3014703	4,9883E-09
Остаток…	71	2,3047E+12	32461016425
Итого	72	3,7428E+12

	Коэфф-ы	Станд. ошиб.	t-стат.	P-Знач.	Ниж. 95 %
Y-пересечение	12730,0376	25434,7819	0,500497217	0,61827295	-37985,477
Z4	2,60309142	0,39109328	6,655934971	4,9883E-09	1,82327357

5. Оценка качества и выбор оптимальной модели

Данный анализ выполняется путем оценки коэффициента детерминации, F-критерий Фишера и средней ошибки аппроксимации.

Коэффициент детерминации и среднюю ошибку аппроксимации рассчитываем аналогично расчету, приведенному в пункте 4.

А) Максимальное значение коэффициента детерминации имеет фактор Z3 (0,75958772). Основываясь на принципе, больше значение коэффициента детерминации, характеризует сильную взаимосвязь между признаками математической модели, наиболее адекватной является модель зависимости прироста ВРП от бюджетных средств (Z3).

Б) Средняя ошибка аппроксимации [2, с.195]

Для расчета средней ошибки аппроксимации анализируются остатки модели (Еi Yi — YТi). Расширим аналитику, добавив в таблицу столбец относительной погрешности, которая рассчитывается по формуле Еотн.i100 с помощью функции ABS.

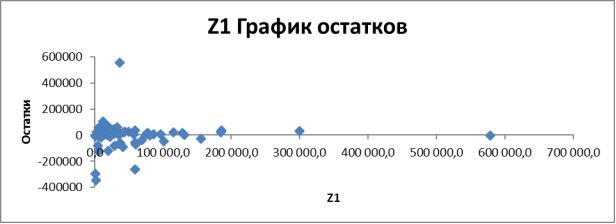
1) Расчет для Z3

Наблюдение	Предсказанное Y2	Остатки	Стад-е остатки	Относ-й остаток	Ei Y2-Yt
1	79545,77526	36559,22644	0,32702913	31,48807192	36 559,23
2	49384,76281	-14940,39568	-0,133644639	43,37543965	-14 940,40
3	22446,90423	12640,43222	0,113071035	36,02562491	12 640,43
4	282545,2124	-179635,0356	-1,60686905	174,5551714	-179 635,04
5	6705,727519	12201,91918	0,109148453	64,53430917	12 201,92
6	29882,79265	17579,66083	0,15725336	37,03908993	17 579,66
7	-11347,59432	26207,94189	0,234434951	176,3615674	26 207,94
8	13228,01371	28731,85229	0,257011802	68,4746045	28 731,85
9	92142,91134	-51136,94141	-0,457429522	124,7060891	-51 136,94
10	240371,2964	189300,2007	1,693325762	44,05696025	189 300,20
11	-3077,634112	28892,99325	0,258453238	111,9217172	28 892,99
12	28192,00664	5505,325664	0,04924617	16,33757122	5 505,33
13	8049,733481	22448,65811	0,200807453	73,60603933	22 448,66
14	37928,00858	1632,601551	0,014603927	4,126836127	1 632,60
15	46088,63557	-8212,043441	-0,073458267	21,68105149	-8 212,04
16	51503,86647	-13114,94266	-0,117315619	34,16335068	-13 114,94
17	61285,82423	-12781,7264	-0,114334937	26,35184855	-12 781,73
18	1264267,21	482716,6866	4,317991204	27,6314331	482 716,69
19	13590,12364	10371,3558	0,092773721	43,28345346	10 371,36
20	6314,395535	77283,22793	0,691312954	92,44668057	77 283,23
21	77014,68178	-4809,507689	-0,043021947	6,660890649	-4 809,51
22	20517,99483	37006,48792	0,331029968	64,33171782	37 006,49
23	38293,81708	-1193,775411	-0,010678545	3,217719865	-1 193,78
24	163956,4378	-83432,62713	-0,746320482	103,6123681	-83 432,63
25	12511,43342	18232,07359	0,163089314	59,30381847	18 232,07
26	1089,75919	22215,21202	0,198719234	95,3239196	22 215,21
27	-5229,370849	21602,08076	0,19323466	131,939556	21 602,08
28	756327,9633	-365710,3814	-3,271347881	93,62363557	-365 710,38
29	-2872,262202	11545,67129	0,103278193	133,1157239	11 545,67
30	-8483,968159	13178,51712	0,117884305	280,7195584	13 178,52
31	555132,4623	-341232,0074	-3,052384239	159,5284159	-341 232,01
32	17137,63499	10433,79388	0,093332241	37,84277532	10 433,79
33	52228,808	19638,82615	0,175672979	27,32638466	19 638,83
34	226381,0751	-114664,1829	-1,025692599	102,6381782	-114 664,18
35	166104,1039	33148,69826	0,296521317	16,63650293	33 148,70
36	1065,267465	14227,96312	0,127271796	93,03438564	14 227,96
37	52305,68856	-29585,58457	-0,264648597	130,217646	-29 585,58
38	353625,7688	-72037,50471	-0,644388977	25,58256643	-72 037,50
39	28924,08595	34866,56304	0,311887939	54,65779639	34 866,56
40	40393,72315	-7817,733341	-0,069931089	23,9984522	-7 817,73
41	101264,8385	83144,65861	0,743744549	45,08697215	83 144,66
42	24378,84126	7787,339365	0,06965921	24,20971098	7 787,34
43	162630,2312	-36521,7049	-0,326693493	28,96053579	-36 521,70
44	30217,3663	70657,76762	0,63204697	70,04478197	70 657,77
45	51259,15219	-20947,447	-0,187378838	69,1067918	-20 947,45
46	89608,01781	55727,51748	0,498493085	38,34404117	55 727,52
47	50649,3229	6297,223957	0,056329848	11,05813136	6 297,22
48	13709,66175	33020,7069	0,29537641	70,66220074	33 020,71
49	14647,96432	5949,885329	0,053222839	28,88595378	5 949,89
50	287667,3432	-56700,50743	-0,507196662	24,54919869	-56 700,51
51	531599,9064	290218,3082	2,596057142	35,31417326	290 218,31
52	111610,9009	19653,1193	0,175800834	14,97220584	19 653,12
53	12758,80323	-8390,44695	-0,07505412	192,0733204	-8 390,45
54	38878,95731	-15819,86697	-0,141511674	68,60577212	-15 819,87
55	-1745,033942	5308,995521	0,04748996	148,9633208	5 309,00
56	-6888,527352	27620,42238	0,247069853	133,2267134	27 620,42
57	51602,11527	-13147,88603	-0,117610304	34,19100134	-13 147,89
58	65762,15493	-22733,77481	-0,203357875	52,83437291	-22 733,77
59	208538,6504	-58258,54234	-0,521133577	38,76663591	-58 258,54
60	37216,60967	52574,46614	0,47028845	58,55199491	52 574,47
61	91999,24234	30859,48962	0,276043917	25,11786434	30 859,49
62	132973,1879	-34335,17097	-0,307134537	34,8092673	-34 335,17
63	38839,49091	32377,451	0,289622365	45,46313017	32 377,45
64	28224,00826	28430,26811	0,254314075	50,18203378	28 430,27
65	147446,4104	-47746,67434	-0,427102948	47,89047217	-47 746,67
66	23648,0869	-12162,29658	-0,108794022	105,8899409	-12 162,30
67	497669,2994	-415149,4521	-3,713589631	503,0904263	-415 149,45
68	85537,78516	-32153,3749	-0,287617963	60,22989624	-32 153,37
69	34409,75876	12176,09671	0,108917466	26,13689625	12 176,10
70	8645,343592	7383,716725	0,06604873	46,06456386	7 383,72
71	27810,21989	86562,20632	0,774315154	75,68450647	86 562,21
72	3603,617132	1826,163059	0,016335371	33,63235702	1 826,16
73	-22269,52799	28627,76305	0,256080704	450,2470063	28 627,76
				76,5523988

Проанализировав данные относительной погрешности, найдем среднее значение отн 76,55 %.

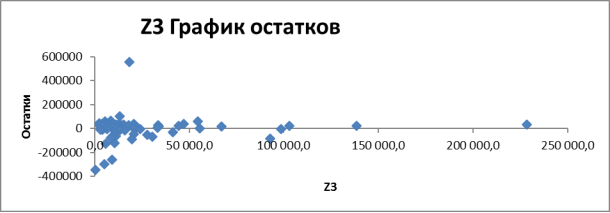
2) Расчет для Z1

Наблюдение	Предсказанное Y2	Остатки	Стандартные остатки	Относительный остаток	Ei Y2-Yt
1	77878,51271	38226,48899	0,262445201	32,92406738	38 226,49
2	26669,90167	7774,465469	0,053375845	22,57107944	7 774,47
3	41311,07056	-6223,734117	-0,042729249	17,73783577	-6 223,73
4	71257,54075	31652,63608	0,217312201	30,75753735	31 652,64
5	12091,47766	6816,169032	0,04679663	36,04980113	6 816,17
6	60104,58692	-12642,13344	-0,086794978	26,63607232	-12 642,13
7	16128,98959	-1268,642023	-0,008709903	8,537095226	-1 268,64
8	22379,74253	19580,12348	0,134427974	46,66393233	19 580,12
9	125964,8768	-84958,90683	-0,583288134	207,1866779	-84 958,91
10	398733,1506	30938,34647	0,212408222	7,200465166	30 938,35
11	18505,54788	7309,811257	0,050185747	28,31574497	7 309,81
12	42062,51406	-8365,181755	-0,057431427	24,8244629	-8 365,18
13	21639,17952	8859,212064	0,060823208	29,04812878	8 859,21
14	29853,41121	9707,198925	0,066645089	24,53753593	9 707,20
15	34862,14398	3014,448144	0,020695792	7,958604444	3 014,45
16	62160,5477	-23771,62389	-0,163204856	61,92313182	-23 771,62
17	64856,19101	-16352,09318	-0,112265827	33,71280761	-16 352,09
18	645157,1322	1101826,764	7,56462743	63,07023016	1 101 826,76
19	18694,01957	5267,459868	0,036163917	21,98303273	5 267,46
20	74938,28453	8659,338932	0,059450973	10,35835539	8 659,34
21	107687,6818	-35482,50775	-0,243606309	49,14122596	-35 482,51
22	53953,5941	3570,888649	0,024516052	6,207598015	3 570,89
23	49280,62042	-12180,57876	-0,083626159	32,83171179	-12 180,58
24	94970,71634	-14446,90565	-0,0991857	17,94115992	-14 446,91
25	28389,10364	2354,403368	0,016164233	7,658213382	2 354,40
26	19415,5234	3889,447803	0,02670313	16,68934825	3 889,45
27	13359,66703	3013,042885	0,020686144	18,40283557	3 013,04
28	247732,2893	142885,2927	0,980983617	36,57932957	142 885,29
29	5366,470951	3306,938135	0,022703891	38,12731652	3 306,94
30	5611,258351	-916,709386	-0,006293698	19,52710245	-916,71
31	396549,4722	-182649,0172	-1,253982759	85,38972825	-182 649,02
32	24331,93142	3239,497451	0,022240875	11,74947249	3 239,50
33	90859,38727	-18991,75311	-0,130388498	26,42601686	-18 991,75
34	118272,5188	-6555,626601	-0,045007867	5,868071044	-6 555,63
35	168046,0423	31206,75983	0,214251023	15,66189258	31 206,76
36	13086,83812	2206,39246	0,015148059	14,42724902	2 206,39
37	20700,89964	2019,204347	0,013862913	8,887302401	2 019,20
38	276551,5597	5036,704336	0,034579657	1,788676937	5 036,70
39	63025,20004	765,4489533	0,005255215	1,199939122	765,45
40	41488,07141	-8912,081608	-0,061186186	27,35782293	-8 912,08
41	163422,9465	20986,5506	0,144083845	11,38040661	20 986,55
42	27282,08131	4884,099317	0,033531942	15,18395788	4 884,10
43	184420,8853	-58312,35901	-0,400345394	46,23982273	-58 312,36
44	123155,7531	-22280,61922	-0,152968315	22,08732554	-22 280,62
45	31424,27005	-1112,564856	-0,00763835	3,67041329	-1 112,56
46	207576,0575	-62240,52221	-0,427314326	42,82539854	-62 240,52
47	76180,57617	-19234,02931	-0,132051853	33,77558496	-19 234,03
48	38112,07194	8618,296715	0,059169196	18,44260374	8 618,30
49	18668,51182	1929,337826	0,013245931	9,366695357	1 929,34
50	282380,2249	-51413,38913	-0,352980293	22,26007425	-51 413,39
51	1245591,435	-423773,2207	-2,909428808	51,56532347	-423 773,22
52	172331,832	-41067,81179	-0,281952395	31,28641932	-41 067,81
53	1059,911356	3308,444922	0,022714236	75,73660919	3 308,44
54	22294,25201	764,838328	0,005251022	3,316862533	764,84
55	1403,558272	2160,403307	0,014832319	60,61803022	2 160,40
56	11157,38839	9574,506642	0,065734086	46,18249624	9 574,51
57	49182,07547	-10727,84623	-0,073652377	27,89770187	-10 727,85
58	19817,09979	23211,28033	0,159357799	53,94411843	23 211,28
59	335281,0931	-185000,985	-1,27013027	123,104107	-185 000,99
60	149926,2547	-60135,17892	-0,412860024	66,97233369	-60 135,18
61	216744,405	-93885,67307	-0,644575137	76,41758268	-93 885,67
62	126300,6423	-27662,62542	-0,189918653	28,04458797	-27 662,63
63	80183,96644	-8967,024527	-0,061563398	12,59113953	-8 967,02
64	76513,31027	-19859,03391	-0,136342842	35,05301838	-19 859,03
65	129613,5242	-29913,78813	-0,205374084	30,00387896	-29 913,79
66	9558,162701	1927,627619	0,01323419	16,78271643	1 927,63
67	62691,40159	19828,44581	0,136132839	24,02869908	19 828,45
68	87747,88289	-34363,47263	-0,235923537	64,36986466	-34 363,47
69	41373,12169	5212,73377	0,035788193	11,18952033	5 212,73
70	12187,16568	3841,89464	0,026376652	23,96830859	3 841,89
71	127432,9031	-13060,47688	-0,089667128	11,41925315	-13 060,48
72	979,2879771	4450,492214	0,030554999	81,96450054	4 450,49
73	3455,554681	2902,680388	0,019928446	45,65229747	2 902,68
				33,03014061

Проанализировав данные относительной погрешности, рассчитаем среднее значение отн 33,03 %.

Используется F-тест, выполним проверку значимости модели регрессии. Для этого произведем сравнение

и критического (табличного)

значений F-критерия Фишера.

Таблица 7

Проверка значимости модели регрессии

Модель	R-квадрат	отн	F
Z3	0,75958772	76,55 %	224,326008
Z1	0,591880745	33,03 %	102,9687582

Точность построенной модели можно оценить как низкую.

Анализ значимости расчетных уравнений с помощью F — критерия Фишера.

Расчетные значения F — статистики представлены в таблице 7. Найдем значение Fкр 4,10 (используя функцию FРАСПОБР, уровень значимости α 5 %, степени свободы k1 1 и k2 38).

Схема проверки

Для уравнения модели Z3: F 1,13917E-23 < Fкр 3,97 (следовательно, не является значимой и ее использование нецелесообразно).

Для уравнения модели Z1: F 1,852E-15 < Fкр 3,97 (следовательно, не является значимой и ее использование нецелесообразно).

Вывод: Основываясь на полученных результатах, нельзя отдать приоритет ни одной из моделей. Целесообразность использования модели с одним фактором для реальной оценки инвестиционной отдачи довольно низкая. Следовательно, рекомендуется использовать двухфакторную модель, полученную ранее.

Общий вывод исследования

Основываясь на проведенном исследовании структуры и динамики инвестиций в основной капитал допустимо сделать следующие выводы:

Полученное уравнение множественной регрессии, его практическое качество, обоснованное высоким значением коэффициента корреляции 0,9007 %, а также представленные выше статистически оценки анализируемых параметров, имеющие высокую тесноту связей с выделенными приоритетными факторными признаками, в полной мере дают возможность судить о степени эффективность процессов инвестирования средств в основной капитал.
Основываясь на полученной модели, выявлен ряд ключевых закономерностей в динамике инвестиционных процессов на территории анализируемых макрорегионов. Самым значащим фактором (источником финансирования), оказывающим влияние, оказались бюджетные средства. С одной стороны, такую динамику можно считать положительной — если сделать предположение о том, что такого рода динамика, следствие жесткого контроля расхода бюджетный средств выделенных на инвестирование, а также четкое планирование и цели ориентированность на динамические сектора экономики. С другой же стороны, такая тенденция настораживает, поскольку наряду с ней, все другие виды инвестирования, хоть и имеют место быть (и довольно в большом объеме), но отдача от вложенных средств, значительно меньше. В любом случае, данный факт требует дополнительных исследований и более детальной проработки.
По ряду регионов было выявлено негативное влияние с позиций слабой инвестиционной активность банков и собственных средств хозяйствующих субъектов. Скорее всего, такого рода ситуация складывается из-за высоких процентных ставок, которые, еще на стадии планирования делают почти любой проект убыточным. С другой же стороны, это объясняется уровнем рентабельности хозяйствующих субъектов и как следствие низкой инвестиционной привлекательностью.
Из динамики распределения максимальных объемов инвестиций, кардинально выделяются центральные регионы Российской Федерации, что также является негативным показателем общей эффективности использования инвестиционных ресурсов на всей территории страны.

Литература:

Орлова, И. В. Экономико-математическое моделирование: Практическое пособие по решению задач / И. В. Орлова. — М.: Вузовский учебник, НИЦ ИНФРА-М, 2013. — 140 c.
Орлова, И. В. Экономико-математические методы и модели: компьютерное моделирование: Учебное пособие / И. В. Орлова. — М.: Вузовский учебник, НИЦ ИНФРА-М, 2011. — 389 c
Статистика: учебник/ под ред. И. И. Елисеевой; СПб гос. ун-т экономики и финансов. — М.: Юрайт, 2010, 2012
Российский статистический ежегодник (2014 год): Федеральная служба государственной статистики [Электронный ресурс]. — Режим доступа: http://www.gks.ru/wps/wcm/connect/rosstat_main/rosstat/ru/statistics/publications/catalog/doc_1135087342078_ (Дата обращения 1.06.2015)
Землянский Д. Ю. Сезонные ритмы социально-экономических процессов в регионах России. Автореферат диссертации на соискание ученой степени кандидата географических наук, Москва, 2011, 26 с.
Практикум по социально-экономической статистике: учебно-методическое пособие/ под ред. М. Г. Назарова; Академия бюджета и казначейства М-ва Финансов Рос. Федерации. — М.: КноРус, 2009.
Попов, А. М. Экономико-математические методы и модели: Учебник для бакалавров / А. М. Попов. — М.: Юрайт, 2013. — 479 c.

Построение эконометрических моделей для анализа эффективности инвестиций в основной капитал (региональный аспект)

Библиографическое описание:

Ключевые слова

Похожие статьи

Применение концепции EVA для оценки инвестиционной привлекательности предприятий строительной отрасли

Оценка инвестиционной привлекательности фирмы

Анализ методологических подходов к оценке капитализации территории

Статистический анализ вариации, финансовых показателей деятельности предприятий сферы ЖКХ г. Оренбурга

Об использовании анализа дивидендной доходности с целью совершенствования инвестиционных стратегий на финансовом рынке

Статистический анализ добычи нефти в Российской Федерации

Статистическое изучение объема розничного товарооборота в РФ

Методы повышения эффективности менеджмента в сфере туристского бизнеса

Эффективность прогнозирования отраслевых индексов методом анализа временных рядов

Оценка эффективности реальных инвестиций для определения целесообразности проекта к реализации (на примере г. Севастополя)