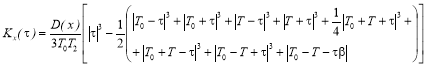В процессе усреднения техногенного сырья ключевыми характеристиками являются дисперсия и корреляционная функция. Дисперсия отражает степень разброса качественных показателей сырья вокруг среднего значения, показывая, насколько сильно различаются порции сырья между собой. Уменьшение дисперсии после усреднения является показателем эффективности процесса. Корреляционная функция описывает взаимосвязь между последовательными порциями сырья, оценивая наличие корреляции в колебаниях их качества. Если корреляционная зависимость между порциями невелика, усреднение становится более эффективным, так как достигается значительное выравнивание характеристик качества. Эти показатели играют важную роль в количественной оценке и прогнозировании эффективности усреднительных систем.
В статье приведено математическое исследования дисперсии и корреляционной функции в процессе усреднения техногенного сырья.
Ключевые слова: техногенное сырье, корреляционная функция, спектральная плотность, дисперсия, смеситель, усреднение.
Усреднение техногенного сырья представляет собой важный этап в процессах горной добычи и переработки, направленный на снижение колебаний качественных характеристик сырья, получаемого из различных источников [1–2]. Этот процесс особенно важен в случае работы с техногенными месторождениями, где качество исходного материала может значительно варьироваться. Основной задачей усреднения является достижение стабильных показателей качества сырья, что положительно сказывается на эффективности дальнейших технологических процессов, таких как обогащение или переработка [3–4].
Теоретическая основа усреднения техногенного сырья включает в себя использование методов математической статистики, теории вероятностей и теории случайных функций для количественной оценки колебаний показателей качества [5]. Основными характеристиками, которые учитываются при усреднении, являются дисперсия и корреляционная функция. Дисперсия отражает разброс данных по качеству сырья, а корреляционная функция описывает взаимосвязь между последовательными порциями сырья [5–8].
Если на выходе представить значение дисперсии
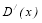
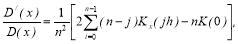
где
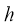
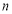
Так, например, если начальный ряд показателей имеет последовательность, а в смеситель поступают порции
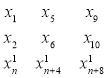
То n=3, а h=4. В смеситель порции техногенного сырья могут подаваться не в той же последовательности, в какой они находятся в потоке техногенного сырья из техногенного сырья, и величина h характеризует интервал нарушения этой последовательности.
Например, когда, смешивание осуществляется в смесителе, вмещающем две порции техногенного сырья, поступившие в разное время.
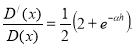
Корреляционная функция показателей качества в порциях техногенного сырья
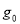
Корреляционная функция показателей качества в порциях техногенного сырья g 0 на выходе из смесителя, когда начальная корреляционная функция аппроксимирована экспоненциальной кривой (III.18) определяется формулами:
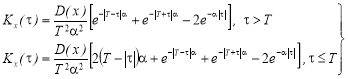
Подставляя в формулу (1) значение корреляционной функции (2), получим
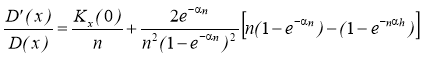
где
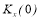
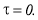
В случае треугольной функции на входе расчет выходной корреляционной функции производится по формуле
|
|
(5) |
Предельная дисперсия на выходе двух видов корреляционной функции определяется подстановкой в них
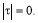
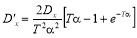
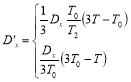
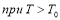
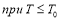
Экспоненциальная корреляционная функция при
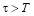
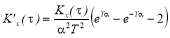
Учитывая, что
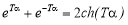
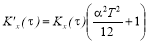
Таким образом, ординаты выходной корреляционной функции для
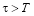
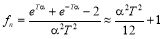
Используя формулы (4), (6) и (7), можно рассчитать степень усреднения техногенного сырья в смесителях различной конструкции: многослойных штабелях, бункерах при различных режимах загрузки и выгрузки и т. д. Анализ формул (1) и (4) показывает, что степень усреднения зависит от емкости смесителя
n
, сдвига фазы
h
и показателя
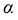
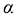
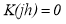
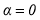
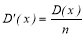
при
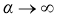
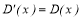
Для всех временных рядов, когда имеется корреляционная связь показателей качества и кривая корреляционной функции располагается на всем протяжении выше оси времени,
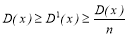
Следовательно, предельный коэффициент усреднения
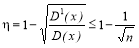
Таким образом, формула 11 характеризует наибольшую степень усреднения, которая может быть достигнута в смесителе вместимостью n. При условии 12 никакого усреднения в смесителе не происходит.
Для примера рассмотрим случайный процесс колебаний содержания металла в техногенном сырье, для которого
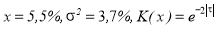
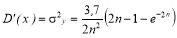
Ниже приведены значения дисперсии и степени усреднения техногенного сырья после склада-смесителя при вместимости смесителя 5–20 партий (таблица 1).
Таблица 1
Результат расчета склада-смесителя
|
Вместимость смесителя, число партий |
5 |
10 |
15 |
20 |
|
Дисперсия после усреднения, % |
0,67 |
0,35 |
0,24 |
0,18 |
|
Степень усреднения, ед. |
2,3 |
3,1 |
3,8 |
4,3 |
Для случайных процессов, представленных обычно суммой колебаний с различными частотами, можно определить характеристическую функцию, которая показывает спектр частот колебательного процесса и распределения амплитуд колебаний по различным частотам колебаний, т. е. определяет частоты, которые слагают поток колебаний и долю этих частот в суммарном потоке колебаний и в общей величине дисперсии.
Корреляционная функция и спектральная плотность дисперсии связаны отношениями
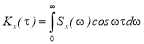
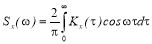
Нормированная корреляционная функция
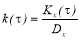
Нормированная спектральная плотность дисперсии
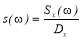
Площадь над кривой спектральной плотности численно равна дисперсии случайной функции, а площадь под кривой нормированной спектральной плотности − единице. Доля дисперсии, образуемая колебаниями с определенной частотой, определяется как доля площади, находящаяся под этим участком кривой нормированной спектральной плотности (рис. 2).
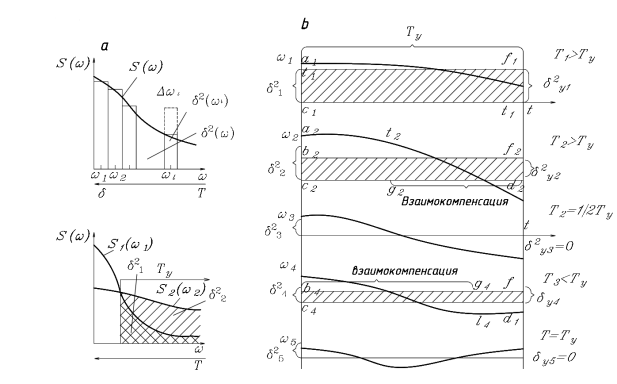
Рис. 2. Физическая сущность спектральной плотности ( a ), связь спектральной плотности ( б ) и периода колебаний ( в ) с продолжительностью усреднения
Аналитически это выражается зависимостью
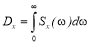
Для корреляционной функции, аппроксимируемой экспоненциальной кривой, спектральная плотность имеет вид:
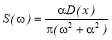
Интегрируя
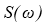
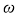
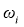
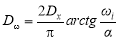
где
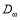
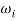
Заменяя
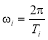
получаем
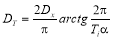
где
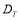
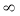
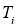
Дисперсия, представленная отклонениями в интервале периодов
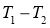
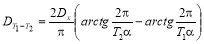
Смеситель вместимостью g c порций уменьшает дисперсию колебаний с периодом T . Коэффициент уменьшения дисперсий определяется по формуле
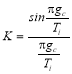
или с достаточным приближением
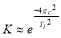
В смесителе достаточно большой емкости полностью погашаются высокочастотные колебания, а колебания с большим периодом сохраняют свою амплитуду.
По приведенным выше формулам определяются
K
для всей совокупности периодов. Остаточная дисперсия после смесителя определяется умножением
K
на
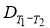
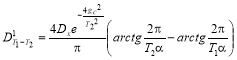
Оценка качества усреднения техногенного сырья на основе теории дисперсии и корреляционной функции позволяет детально анализировать процессы формирования стабильных качественных характеристик сырья. Теоретические методы, основанные на дисперсии, дают возможность количественно оценить степень вариации показателей качества между порциями сырья, в то время как корреляционная функция позволяет выявить взаимосвязи между последовательными партиями.
Литература:
- Андреев В. Н. Теория дисперсии и корреляции в задачах усреднения качества сырья. — М.: Недра, 2005. — 320 с.
- Борисов С. В. Методы математической статистики в горной промышленности // Горный вестник. — 2007. — Т. 8, № 2. — С. 35–42.
- Иванов П. А. Колебания качества техногенного сырья при разработке карьеров // Математическое моделирование процессов добычи. — СПб.: Горный университет, 2010. — С. 56–63.
- Кузнецов А. И. Основы теории корреляции и их применение в горнодобывающей отрасли // Труды Международной конференции по горному делу. — Екатеринбург: УГГУ, 2009. — С. 128–135.
- Михайлов Е. Н. Уравнения дисперсии для оценки показателей качества техногенного сырья // Вестник науки и техники. — 2006. — Т. 12, № 3. — С. 98–104.
- Петрова Л. В. Использование методов корреляции для оптимизации усреднения сырья [Электронный ресурс]. — Режим доступа: http://www.miningjournal.ru (дата обращения: 01.10.2024).
- Смирнов Д. В. Применение теории случайных функций в моделировании усреднительных процессов // Математика и горное дело. — 2008. — Т. 6, № 4. — С. 78–83.
- Федоров И. В. Дисперсия и корреляция в процессе усреднения // Горная техника. — 2012. — Т. 15, № 1. — С. 25–30.