Усреднение техногенного сырья является процессом, направленным на уменьшение вариаций в качестве сырья путем объединения и перемешивания различных порций. Этот метод позволяет выравнивать показатели качества, такие как содержание полезных компонентов, что необходимо для обеспечения стабильности технологических процессов переработки и дальнейшего использования материалов. Основной целью усреднения является минимизация отклонений качественных показателей для повышения эффективности и рентабельности производственных процессов. Важную роль в этом процессе играют математические методы и статистические показатели, такие как дисперсия потока, математическое ожидание и корреляционная функция, которые помогают количественно оценить колебания в качестве сырья до и после усреднения.
В статье приведено математическое описание усреднения качества техногенного сырья посредством зависимости дисперсии потока, математического ожидания и корреляционной функцией.
Ключевые слова: техногенное сырье, корреляционная функция, математическое ожидание, предварительное дозирование, управляемое смешивание, показатель качества.
Усреднение качества техногенного сырья представляет собой технологический процесс, направленный на конкурентные качественные характеристики ресурса с целью достижения стабильных результатов, соответствующих установленным техническим требованиям. Основная цель усреднения — снижение колебаний показателей, таких как содержание компонентов или примесей, для обеспечения конкурентоспособности и надежности последовательного перерабатывания технологических процессов.
На рис. 1 показаны графики, характеризующие особенности изменения во времени качества техногенного сырья двух потоков.
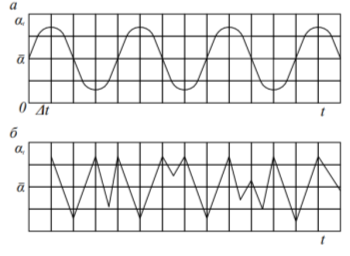
Рис. 1. Изменение качества техногенного сырья во времени
В первом (а) и во втором (б) примерах
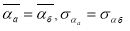
Для первого потока техногенного сырья коэффициент взаимной корреляции показателей качества в смежных партиях больше, чем во втором.
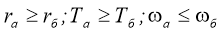
где
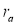
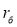
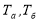
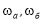
Повышение коэффициента взаимной корреляции и периода колебания приводит к более тесной становится связь показатели качества техногенного сырья
Нужное качество техногенного сырья можно достигнуть путем:
– предварительного дозирования техногенного сырья разного качества с целью обеспечения заданного базового уровня, или управляемое смешивание;
– без предварительного дозирования разных сортов техногенного сырья или неуправляемое смешивание.
Управляемое смешивание осуществляется при выделении отдельных сортов техногенного сырья, направляемое — без предварительного разделения техногенного сырья на сорта. Управляемое смешивание возможно при наличии сортовых аккумуляторов добытого техногенного сырья. Эти аккумуляторы могут представлять собою склад техногенного сырья на колёсах или сортовые склады (бункера).
Осуществляя дозирование техногенного сырья на базовый (плановый) уровень качества путем подачи разных сортов из аккумуляторов в заданной пропорции, направляют поток техногенного сырья в смесители (склады-смесители, бункера-смесители), в которых происходит глубокое смешивание. При смешивании с предварительным дозированием достигается заданное (плановое) усреднение качества техногенного сырья в заданном объеме. При смешивании без предварительного дозирования достигается однородность смеси, но средний показатель качества в усредненном объеме может отличаться от базового (планового). В случае управляемого смешивания информация о техногенном сырье, поступающей в смеситель, включает данные о доле отдельных поступлений и показатели, характеризующие среднее качество техногенного сырья в отдельных поступлениях
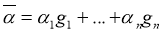
Если известно среднее квадратическое отклонение показателей, характеризующих качество отдельных поступлений
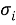
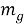
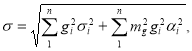
где
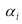
Рассмотрим применение математической статистики и теории случайных функций при процессе усреднения качества техногенного сырья. Представим, что техногенное сырье транспортируется
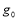
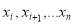
Дисперсия потока техногенного сырья представляется следующей функцией
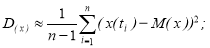
где
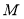
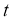
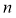
Математическое ожидание
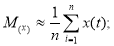
Необходимо обратить внимание, что две функции (3) и (4) недостаточно для описания случайных процессов. При одинаковых математическом ожидании и дисперсии два случайных процесса могут отличаться частотной структурой. В одном случае будет происходить медленное плавное изменение показателя качества, а в другом, например, за этот же промежуток времени, произойдет неоднократное резкое изменение показателя.
Для более корректного отображения усреднения необходимо добавить корреляционную функцию случайного процесса с указанием временного интервала.
Наиболее часто корреляционную функцию представляют в виде экспоненциальных кривых
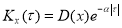
Или треугольных зависимостей
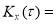
где
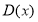
Корреляционные функции быть представлены и более сложными уравнениями в виде суперпозиции экспоненциальных и периодических кривых. Корреляционные функции в виде периодических кривых образуются в том случае, когда поток показателей представляет собой совокупность нескольких сравнительно однородных потоков, математическое ожидания, которых различны. Случайные функции, как и процесс колебаний, которые они отражают, как правило, поли гармоничны и включают в себе колебания, имеющие разные частоты или периоды.
Для подавляющего числа случаев экспоненциальной аппроксимации корреляционной функции бывает достаточно для расчетов, связанных с усреднением техногенного сырья.
При этом доля n техногенного сырья массой
Литература:
- Басараб, Г. Г., Пак, В. В. Теория вероятностей и математическая статистика. — М.: Высшая школа, 2007. — 432 с.
- Гмурман, В. Е. Руководство по теории вероятностей и математической статистике. — М.: Юрайт, 2012. — 512 с.
- Зубов, А. И. Методы обработки данных в статистике и эконометрике. — М.: Финансы и статистика, 2013. — 398 с.
- Коровкин, Н. В., Коровкин В. Н. Основы математического моделирования в горной промышленности. — СПб.: Лань, 2010. — 35
- Саати, Т. Л. Принятие решения. Метод анализа иерархий. — М.: Радио и связь, 1993. — 278 с.
- Смирнов, Н. В. Статистика и обработка экспериментальных данных. — М.: Наука, 2010. — 414 с.
- Федоренко, Р. П. Методы оптимизации производственных процессов в горной промышленности. — М.: Недра, 2014. — 392 с.
- Хендерсон, Д. М., Рейд, К. С. Методы математической статистики для инженеров. — М.: Либроком, 2018. — 300 с.
- Чернов, С. В. Анализ и обработка данных на основе теории случайных функций. — СПб.: Питер, 2011. — 288 с.
- Ширяев, А. Н. Вероятность: Курс лекций. — М.: МЦНМО, 2017. — 560 с.
- Юшков, М. П. Теория и практика горного производства. — Екатеринбург: Уральский государственный горный университет, 2015. — 470 с.
- Кузнецов, А. С. Технология разработки техногенных месторождений полезных ископаемых. — М.: Горная книга, 2014. — 354 с.

