Исследование устойчивости оползневого склона участка железной дороги



В статье рассматривается актуальная проблема, свойственная для линейных объектов, в том числе железных дорог, обеспечение устойчивости земляного полотна железных дорог в оползнеопасных районах, снижение (устранение) негативного воздействия оползней, оценка оползневой опасности с использованием современного математического аппарата для безопасного и бесперебойного движения поездов.

Ключевые слова: оползень, устойчивость склона, смещение, запас прочности.

Воздействие человека на окружающую природную среду вызывает изменения в ней, которые негативно влияют на человеческое общество. Строительство новых железных и автомобильных дорог в горных районах, увеличение из года в год движения транспортных средств, особенно тяжелых, являются причиной возникновения опасного геологического процесса. Инфраструктура водных и сельскохозяйственных объектов, горнодобывающих предприятий, жилых комплексов, которые строятся и эксплуатируются в горных районах, приводит к увеличению воздействия нерациональных нагрузок на отдельные участки урбанизированных горных районов, а также к образованию новых оползнеопасных зон.

Вокруг нас возникает природно-техническая система (ПТС), т. е. совокупность форм и состояний взаимодействия природной среды с инженерными сооружениями на всех стадиях их функционирования. Природно-техническая система имеет границы и представляет собой совокупность инженерного сооружения (комплекса сооружений) с частью геологической среды в зоне его (их) влияния [1]. Вопрос определения границ довольно сложный, но, как правило, нижняя граница соответствует глубине проникновения в литосферу техногенного воздействия, верхняя находится в приповерхностной части литосферы. Таким образом, любая природно-техническая система как целостная и упорядоченная во времени и пространстве совокупность взаимодействующих компонентов, включает в себя продукты и средства труда, естественную или искусственно измененную природную среду. Например, на железной дороге выемка сформирована техногенным воздействием и по сути составляет часть геологической среды, или насыпь сложена природным, но техногенно-нарушенным грунтом. В целом же, откосы, выемки и насыпи, полотно железных и автомобильных дорог образуют единый комплекс в составе ПТС — транспортные природно-технические системы (ТПТС) с присущими им инженерно-геологическими процессами [2]. Такие процессы и явления, возникающие в геологической среде при техногенных воздействиях, принято считать природно-техногенными.

Большинство новых железных дорог, строящихся в мире за последние полвека, строятся в сложных климатических и топографических условиях. Районы строительства этих железных дорог сейсмически активны или подвержены оползням. Обеспечение устойчивости земляного полотна железных дорог в оползнеопасных районах, снижение (устранение) негативного воздействия оползней, разработка методики оценки оползневой опасности с использованием современного математического аппарата являются актуальными для безопасного и бесперебойного движения поездов.

Устойчивость склона или котлована является одной из наиболее часто встречающихся задач в инженерно-геологическом строительстве. Склон всегда имеет потенциальную энергию собственного веса из-за силы тяжести, и если на склон действуют внешние силы, такие как поровое давление, приложенная нагрузка, землетрясение, волновая сила и т. д., это сильно влияет на его устойчивость. Здесь разрушение склона может произойти, когда активная сила склона превышает силу сопротивления грунта. Анализ устойчивости склона оценивает устойчивость к разрушению, используя соотношение между активной силой и силой сопротивления склона.

В последнее время продолжаются активные исследования по применению метода конечных элементов в качестве метода оценки устойчивости, например, разрушения на склоне, с использованием сильных сторон конечных элементов, таких как простота проверки деформированной формы, даже при различных нагрузках и граничных условиях.

В GTS NX применимыми методами анализа устойчивости откосов, использующими метод конечных элементов, являются метод снижения прочности и метод анализа напряжений, основанный на теории предельного равновесия.

Анализ устойчивости склона методом конечных элементов представляет собой подробные приближенные решения, удовлетворяющие всем силовым условиям равновесия, условиям совместимости, определяющим уравнениям и граничным условиям каждой точки склона. Этот метод численного анализа позволяет моделировать практически реальные формы отказов, лучше отражать полевые условия и детально анализировать минимальный коэффициент запаса прочности и поведение склона при отказе. В частности, процесс разрушения автоматически моделируется без каких-либо предположений относительно плоскости разрушения склона.

Метод снижения прочности (метод анализа устойчивости склона, основанный на методе конечных элементов) постепенно уменьшает прочность на сдвиг и выполняет анализ до тех пор, пока расчет не перестанет сходиться. Эта точка считается точкой разрушения склона, а максимальный коэффициент снижения прочности в этой точке рассматривается как минимальный коэффициент запаса прочности склона. Этот метод является ресурсозатратным, поскольку требует проведения нескольких нелинейных анализов, но может обеспечить более точные результаты за разумное время и повысить скорость обработки данных. Кроме того, метод снижения прочности позволяет проверить процесс деформации от начальной деформации до разрушения без каких-либо необходимых предположений относительно плоскости разрушения.

Теория снижения прочности (SRM). Чтобы смоделировать разрушение на склоне с использованием метода снижения прочности, коэффициент запаса вычисляется в произвольной точке, где круг Мора соприкасается с границей разрушения, как показано на рисунке ниже. Напряженное состояние в этой точке можно определить, как состояние разрушения, и когда эта точка разрушения увеличивается, происходит общее обрушение склона. Анализ методом конечных элементов в этом предельном состоянии расходится, и коэффициент безопасности в этой точке определяется как минимальный коэффициент безопасности.

В методе снижения прочности используются модели материалов: Кулон-Мора, Кулон-Друкера-Прагера и модифицированный Кулон-Мора. Что касается входных переменных, используемых здесь, предполагается, что все переменные имеют постоянное значение, за исключением сцепления, угла трения и угла дилатации, которые определяют разрушение при сдвиге. Когезия, угол трения и угол дилатации, соответствующие элементам грунта (плоская деформация, осесимметричный, твердый), постепенно уменьшаются.

Снижение прочности методом длины дуги (SAM). Основное отличие между существующим методом снижения прочности и методом, использующим метод длины дуги, заключается в методе увеличения/уменьшения коэффициента безопасности, который является стандартом для снижения прочности. Существующий метод вычисляет коэффициент безопасности следующего шага, контролируя коэффициент безопасности текущего шага пользователем определенным приращением. Таким образом, происходит неэффективное вычисление для очень стабильных моделей или нестабильных моделей без суждения инженера, поскольку увеличивается равномерный коэффициент безопасности. Однако, используя метод длины дуги, длина дуги вычисляется с учетом скорости сходимости предыдущего шага, и таким образом можно получить более подходящее приращение коэффициента безопасности.

Использование двух методов оценки устойчивости склонов позволяет получить максимально полную картину и иметь вариативность при применении тех или иных инженерных средств повышения устойчивости откоса. Необходимо отметить, что методом SRM просчитывается общая устойчивость склона, с автоматическим выявлением наименьшего коэффициента устойчивости на наименее устойчивом участке всего склона. Тогда как метод SAM требует заранее определить область центров и касательных для расчета виртуальной поверхности скольжения.

Статические расчёты напряжённо-деформированного состояния выполнены методом конечных элементов. Решение краевой задачи о напряженно-деформированном состоянии расчетной области при использовании метода конечных элементов сводится к численному решению системы уравнений:

[K]{u} = {F}

где: [K] — матрица жесткостей;

{u} — вектор узловых перемещений;

{F} — вектор нагрузок.

Исходные данные для выполнения расчета приняты в соответствие с отчетом об инженерно — геологических изысканиях по объекту: «Строительство железнодорожной линии «Ташгузар — Бойсун — Кумкурган». Участок «Ташгузар — Акрабат». Оползневый склон на 103 км перегона «Чашмаихафизон — Акрабат» (далее «Отчет ИГИ»). На основе исходных данных было построено две 2D модели системы «оползень-основание», на основании наиболее характерных инженерно-геологических разрезов, представленных в Отчете ИГИ (разрезы 1–1 и 3–3).

Согласно Отчету ИГИ представлены следующие характеристики оползня:

1. По морфологическим критериям относится к детрузивному, консеквентному оползню циркообразного типа;
2. Ширина оползня, протяженность по бровке отрыва (трещина отрыва) ~ 400 м;
3. Длина оползня, (по направлению движения) от бровки отрыва до ж. д. линии, около 500 м;
4. Предполагаемая средняя площадь оползневого тела — 400 м*500 м=200 000 м ² ;
5. Предполагаемая мощность оползневого тела изменяется от 4,5–7,0 м в верхней части до 10,0–12,0 м в серединной и нижней части, в среднем составляет около 8,0 м, в нижней части вероятно ограничивается подошвой выемки;
6. Тело оползня сложено глиной аргиллитовой, выветрелой, пестроцветной, от темно-серого до желто-коричневого и темно-фиолетового цвета с оранжевыми прожилками, выветрелой, с включениями гипса в виде кристаллов, с включением обломков ракушек, с включением щебня песчаника, с пятнами и прожилками ожелезнения, твердой, от комковатой до слоистой.
7. Оползневый процесс происходит по ослабленным зонам в глинах, вероятнее всего по поверхностям напластования.
8. Абсолютные отметки в районе бровки срыва (голова оползня) изменяются от 1505 до 1522 м;
9. Абсолютные отметки в нижней части склона (предполагаемая подошва оползня) изменяются от 1443 до 1449 м;
10. Крутизна склона ~ 10–150;
11. Угол падения глинистых пород ~ 20–300;
12. Азимут падения глин — северо-восток 400.

Многовариантные расчеты по определению общего перемещения, напряжения по осям Х и У , а также устойчивости проведены для следующих расчетных случаев:

Расчет устойчивости оползневого склона выполнен для двух инженерно-геологических разрезов в двух вариантах (мокрый склон и сухой склон) с учетом сейсмического.

В расчетах учтены следующие типы нагрузок:

— собственный вес;

— равномерно-распределенная нагрузка по гребню ж/д насыпи;

— нагрузка от сейсмического воздействия.

Каждый вариант просчитан в случае сейсмического воздействия (8 баллов). Сейсмическое воздействие задавалось по эпюре сейсмических ускорений. Максимальные значения в долях от g составили 0,1562 g.

Расчет устойчивости выполнен в расчетном комплексе MIDAS GTS NX. Это программное обеспечение предназначено для анализа геотехнических, инженерных и научных задач.

Для задания грунтов в ПК Midas GTS NX использовалась модель Мора-Кулона. При расчетах в Midas GTS NX были использованы следующие методы расчетов устойчивости склонов:

— Метод редукции (SRM): нелинейный метод расчета путем снижения прочности в конечно-элементной модели.

— Метод анализа напряжений (SAM): Метод основан на решении нелинейной конечно-элементной задачи с использованием теории предельного равновесия.

Описание модели, основанной на разрезе 1–1. Габаритные размер блока грунтового основания составляют 511 х 93 м, с понижением по высоте до 34 м после оползневого массива. Разработанная модель аппроксимирована плоскими (2D) узловыми конечными элементами 2-го порядка. Общее количество конечных элементов в модели — 18499, узлов — 18755 (рис. 1).

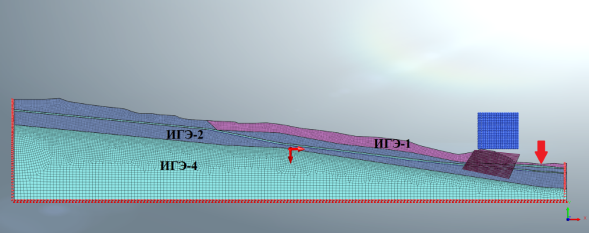
Рис. 1 Расчетная модель по разрезу 1–1

Результаты моделирования оползня склонного массива по разрезам 1–1 и 3–3, с использованием ПК Midas GTS NX с использованием модели Мора-Кулона для задания грунтов приведены на рис. 2–4.

Коэффициент запаса устойчивости сухого склона разреза 1–1 рассчитанный по методу SAM составляет 2,3 и по методу SRM — 3,1 (рис.2).

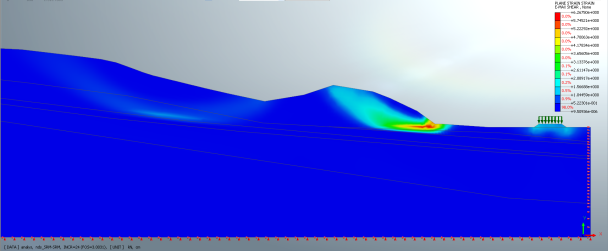
Рис. 2. Расчет устойчивости сухого склона разреза 1–1 с учетом ж/д насыпи

Максимальное перемещения при расчете напряженно-деформированного состояния (НДС) сухого склона с учетом сейсмического воздействия по оси Х достигают около 46 см у верха оползневого участка (рис. 3). В свою очередь максимальные перемещения по оси Y достигают около 37 см в углу модели, тогда как 90,3 % перемещений модели составляют около 6 мм.

Коэффициент запаса сухого склона разреза 1–1 с учетом сейсмического воздействия рассчитанный по методу SAM составляет 1,6 и по методу SRM — 1,51.

Необходимо отметить, что расчет сухого склона по методу SAM выполнен исключительно для вала выпирания неустойчивого оползневого массива, тогда как метод SRM автоматически определяет наиболее неустойчивые участки и растягивающие усилия в массиве методом снижения прочности.

Расчеты по определению общего напряжения без сейсмического воздействия по осям Х и У , а также устойчивости выполнены методами SRM и SAM для мокрого склона с использованием расчетной модели по разрезу 1–1(табл.1).

Коэффициент запаса, рассчитанный по методу SAM, составляет 1.65 и по методу SRM — 2,2.

Аналогичные расчеты по определению общего напряжения по осям Х и У, устойчивости склона, а также деформации в плоском напряженном состоянии по оси X и У выполнены методами SRM и SAM для мокрого склона с использованием расчетной модели по разрезу 1–1 с учетом сейсмического воздействия.

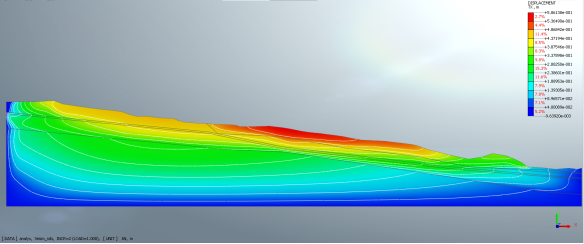
Рис. 3. Изополя перемещений по оси Х при расчете напряженно-деформированного состояния (НДС) мокрого склона с учетом сейсмического воздействия

Максимальные перемещения сухого склона с учетом сейсмического воздействия достигают около 41 см в углу модели, тогда как 97,1 % перемещений модели составляют от 0.8 до 5.3 см. обозначенный на рис. 4 синим цветом.

Рис. 4. Изополя перемещений по оси Y при расчете напряженно-деформированного состояния (НДС) сухого склона с учетом сейсмического воздействия

Анализ результатов расчетов позволил установить, что коэффициент запаса, рассчитанный по методу SAM, составляет 1,12 и по методу SRM — 1,27.

По результатам выполнения расчетного обоснования были получены результаты устойчивости склонов оползневого массива и напряженно-деформированного состояния для четырех вариантов с учетом сейсмического воздействия и с ж/д насыпью (табл.2).

Таблица 1

Коэффициенты устойчивости откосов для вариантов № 1, № 2, № 3 и № 4. Основное сочетание нагрузок (без учета сейсмического воздействия)

	Название расчетного случая	Основное сочетание нагрузок
		Метод SRM	Метод SAM
1	Вариант № 1 (Разрез 1–1, сухой склон)	K уст =2,3	K уст =3,1
2	Вариант № 2 (Разрез 1–1 мокрый склон)	K уст =2,2	K уст =1,65
3	Вариант № 3 (Разрез 3–3 сухой склон)	K уст =2,8	K уст =2,33
4	Вариант № 4 (Разрез 3–3 мокрый склон)	K уст =1,9	K уст =1,59
5	Вариант № 1 + ж/д насыпь (Разрез 1–1, сухой склон)	K уст =2,28	K уст =3,0
6	Вариант № 2 + ж/д насыпь (Разрез 1–1 мокрый склон)	K уст =2,01	K уст =1,65
7	Вариант № 3 + ж/д насыпь (Разрез 3–3 сухой склон)	K уст =2,8	K уст =2,33
8	Вариант № 4 + ж/д насыпь (Разрез 3–3 мокрый склон)	K уст =1,9	K уст =1,59

Таблица 2

Коэффициенты устойчивости откосов для вариантов № 1, № 2, № 3 и № 4. (Особое сочетание нагрузок с учетом сейсмического воздействия)

	Название расчетного случая	Основное сочетание нагрузок
		Метод SRM	Метод SAM
1	Вариант № 1 (Разрез 1–1, сухой склон)	K уст =1,51	K уст =1,6
2	Вариант № 2 (Разрез 1–1 мокрый склон)	K уст =1,27	K уст =1,12
3	Вариант № 3 (Разрез 3–3 сухой склон)	K уст =1,47	K уст =1,66
4	Вариант № 4 (Разрез 3–3 мокрый склон)	K уст =1,21	K уст =1,16
5	Вариант № 1 + ж/д насыпь (Разрез 1–1, сухой склон)	K уст =1,51	K уст =1,6
6	Вариант № 2 + ж/д насыпь (Разрез 1–1 мокрый склон)	K уст =1,27	K уст =1,11
7	Вариант № 3 + ж/д насыпь (Разрез 3–3 сухой склон)	K уст =1,46	K уст =1,65
8	Вариант № 4 + ж/д насыпь (Разрез 3–3 мокрый склон)	K уст =1,20	K уст =1,15

Согласно полученным данным можно сделать вывод, что на участке оползневого склона на 103 км перегона «Чашмаихафизон — Акрабат» возможен риск обрушения. Несмотря на то, что коэффициенты запаса устойчивости, рассчитанные по методу SRM имеют достаточные показатели, метод SAM показывает, что запаса устойчивости мокрого склона при сейсмическом воздействии недостаточно.

Сравнение вариантов с учетом и без учета влияния железнодорожной насыпи и соответствующей нагрузки от состава показывают, что коэффициент запаса устойчивости имеет тенденцию к уменьшению, особенно в случаях с сейсмическим воздействием.

Однако необходимо отметить, что оценка риска оползневого массива выполнена без учета движения по склону потока селей, что безусловно, ухудшит фактическую ситуацию устойчивости склона.

Литература:

1. Епишин В. К. Особенности взаимодействия геологической среды и инженерных сооружений / В. К. Епишин, В. Т. Трофимов // Теоретические основы инженерной геологии. Социально-экономические аспекты / Под ред. акад. Е. М. Сергеева. — М.: Недра, 1985. — С. 32–36.
2. Безуглова Е. В. Оползневая опасность и риск смещений грунтов на склонах: дисс. … канд. техн. наук: 25.00.08 / КубГАУ. — Краснодар, 2005. — 200 с.
3. Методические рекомендации по оценке рисков на железнодорожной инфраструктуре ОАО «РЖД» / ОАО «РЖД». — М., 2011. — 109 с.
4. Djabbarov, S. T., & Mukarramov, R. H. (2023). Influence of engineering and geodynamic processes on stability of transport infrastructure. In E3S Web of Conferences (Vol. 401, p. 01082). EDP Sciences.
5. Djabbarov, S. T., & Mukarramov, R. H. (2021). The monitoring of dangerous exogen geological processes using the 3D scanner. The Scientific Journal of Vehicles and Roads, 2021(2), 50–59.