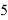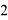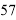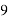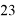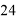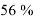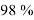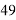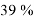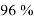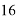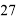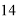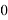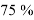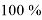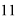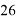В статье представлены как общие методические подходы к обучению решению олимпиадных задач по информатике , так и методика обучения решению задач. В качестве решения олимпиадных задач предлагается результат применения цифровой образовательной среды. Также разработан элективный курс для подготовки к олимпиаде. В элективном курсе обучают решению олимпиадных задач с помощью «жадного» алгоритма, методов динамического программирования и схемы С. А. Оршанского.
В ходе исследования были изучены теоретические аспекты применения методов решения олимпиадных задач при организации элективного курса. В 8–11 классах было проведено экспериментальное исследование относительной эффективности этих методов. Результаты исследования подтверждают значительное повышение готовности обучающихся к олимпиаде, что позволяет использовать эти методы в образовательном процессе для повышения результатов подготовки к олимпиаде.
В исследовании использовались общие методы исследования, такие как анкетирование, анализ, синтез, интерпретация данных.
Ключевые слова: предмет информатики, олимпиадные задачи, цифровое образование, динамическое программирование, схема решения задачи.
Введение
Основные принципы решения олимпиадных задач по информатике в школе включают тщательный анализ условий задачи, разработку эффективного алгоритма, тестирование и упорядочение программы. Важно сосредоточиться на выборе соответствующих методов и структур данных, а также обучить учащихся навыкам оптимизации решений для повышения их эффективности.
Регулярная практика и участие в олимпиадах способствуют развитию необходимых навыков и повышению конкурентоспособности учащихся.
Глава государства Касым-Жомарт Токаев на республиканском съезде педагогов 2023 года поставил перед педагогами четкую задачу — увеличить количество победителей предметных олимпиад, наряду с передовым образованием и воспитанием [1].
Предметные олимпиады — это разновидность интеллектуальных соревнований школьников в определенной научной сфере. Он проверяет не только уровень успеваемости учащихся, но и способность учащихся применять нестандартные знания высокой сложности, решая задания. Предметные олимпиады всегда являются важнейшим видом педагогической деятельности. Ведь именно они выявляют наиболее способных и одаренных детей, развивают образовательные потребности личности и формируют навыки самостоятельной работы [2].
Олимпиады являются важным фактором поиска и отбора талантливой молодежи для формирования будущей интеллектуальной элиты страны.
Олимпиады по информатике требуют от участников решения сложных задач, что способствует развитию аналитического мышления и умения критически оценивать информацию, поиску нестандартных решений. Решение задач на Олимпиадах требует логического мышления, что помогает улучшить навыки решения задач учащихся. Знания и навыки, полученные при подготовке и участии в Олимпиадах, могут быть ценными в профессиональной области, особенно в областях, связанных с информатикой и инженерией.
Эти мероприятия предоставляют одаренным учащимся уникальные возможности для демонстрации своих способностей на национальном и международном уровнях. Участие в таких соревнованиях способствует не только обучению, но и развитию личности, повышению уверенности в себе и способности работать в команде [3].
В 2015 году олимпиада IOI проводилась в Казахстане в г. Алматы. В этом соревновании приняли участие 83 страны. Количество призовых мест, завоеванных Казахстаном на международной олимпиаде по информатике, представлено в таблице 1 [4].
Таблица 1
Количествоучащихся , занявших призовыеместа на ОлимпиадеIOI
|
Годы |
1 место |
2 место |
3 место |
Всего |
|
1999–2004 |
1 |
6 |
7 | |
|
2005–2010 |
2 |
4 |
12 |
18 |
|
2011–2015 |
9 |
6 |
15 | |
|
2016–2020 |
1 |
7 |
9 |
17 |
|
2021–2023 |
3 |
7 |
10 |
Международная жаутыковская Олимпиада — ежегодное соревнование по информатике, физике и математике для учащихся 10–11 классов проводится в Казахстане с 2005 года. В олимпиаде принимают участие команды из разных стран не более 7 человек: 3 представителя по математике, 2 представителя по физике и 2 представителя по информатике. Олимпиада по каждому предмету проводится в два тура. В I и II турах по информатике участники решают задачи.
Количество учащихся, занявших призовые места на Международной Жаутыковской олимпиаде по информатике Казахстана, представлено в таблице 2 [5].
Таблица 2
Количествоучащихся , занявших призовыеместа на МеждународнойЖаутыковскойолимпиаде
|
Годы |
1 место |
2 место |
3 место |
Всего |
|
2020 |
1 |
6 |
15 |
22 |
|
2021 |
1 |
12 |
13 |
26 |
|
2022 |
2 |
14 |
21 |
37 |
|
2023 |
2 |
6 |
19 |
27 |
|
2024 |
3 |
10 |
17 |
30 |
Участие Казахстана в олимпиадах по информатике уже много лет показывает стабильный рост и успешные результаты. За последние пять лет увеличилось количество первых мест, завоеванных Казахстаном, что свидетельствует об улучшении мастерства и подготовки участников. 2024 год особенно примечателен тремя первыми местами.
Такой прогресс свидетельствует о том, что в Казахстане развиваются и совершенствуются образовательные программы и подготовка к олимпиадам, что способствует повышению конкурентоспособности учащихся на международной арене. Однако для достижения более высоких результатов необходимо продолжить совершенствование методов обучения и подготовки, внедряя новые технологии и подходы, а также обеспечивая доступ к дополнительным ресурсам и профессиональной поддержке.
Многолетний опыт показывает, что основной вопрос подготовки школьников к олимпиадам — содержание тем информатики по типовому учебному плану 1–11 классов, утвержденному приказом Министра образования и науки Республики Казахстан от 3 августа 2022 года № 348, недостаточно для решения олимпиадных задач. Подготовка к олимпиадам по информатике является самостоятельным учебным разделом по теоретическим и практическим вопросам, выходящим за рамки школьной программы и требующим особого уровня [6].
Материалыиметодыисследования
Исследовательская работа состояла из этапов выявления проблемы, анализа и систематизации данных, обсуждения результатов исследования. Разработана работа с научной литературой по методическим подходам к решению олимпиадных задач по информатике.
Особое внимание было уделено использованию цифровой образовательной среды для организации элективного курса, направленного на совершенствование навыков учащихся в решении олимпиадных задач по информатике. В рамках курса учащихся учатся решать задачи олимпиады с помощью «жадного» алгоритма, динамического программирования и методов С. А. Оршанского.
В учебном процессе использовались специализированные программные инструменты и платформы для написания, тестирования и упорядочивания кода, что позволило повысить эффективность учебного процесса. Кроме того, был проведен опрос учащихся. Это позволило объективно оценить их мнение об участии в олимпиадах по информатике.
Результатыисследованийиобсуждения
В исследованиях Н. С. Лейтеса, С. Л. Рубинштейна, А. А. Русакова и др. отмечается, что развитие способностей и умений учащихся, овладение предметной областью зависит от образовательной среды и применяемых средств обучения. К выявлению способных и одаренных учащихся относятся внедрение их представлений о деятельности, рост инновационных процессов, олимпийская педагогика [7].
В своих работах Н. В. Чудова и А. А. Дольныкова доказали, что при изучении личностных особенностей и личностных качеств квалифицированных программистов для них характерна настойчивость, стремление к созданию собственного виртуального мира, а также отказ от запретов и барьеров, существующих в реальном мире. Ключом к успешной работе программиста признаются следующие особенности: интровертиролирование, глубина собственных интеллектуальных переживаний, способность к дистанцированию и отступлению [8].
Согласно общепризнанной идее, программист должен обладать высоким уровнем интеллекта и обладать 4 качествами, такими как абстрагирование и понимание отношений между элементами, анализ и систематизация работы. Критичность, склонность к планированию, гибкость мышления, способности к самообучению и переподготовке также присущи ИТ — специалисту. Как отмечают исследователи в области профессиональной подготовки программистов, указанные качества у каждого человека проявляются по-разному. Соответственно, возникает ряд проблем и трудностей в подготовке и обучении.
В исследованиях ученых Е. И. Бидайбекова, Г. Б. Камаловой, В. В. Гриншкуна, М. А. Заганбетовой, О. Ю. Заславской и др. рассматриваются вопросы подготовки учащихся к Олимпиаде, изменения цели, содержания подготовки к Олимпиаде и др. В связи с необходимостью непрерывного совершенствования уровня знаний [9].
Для всестороннего анализа методики решения олимпиадных задач по информатике в школе необходимо учитывать исследования других авторов. Например, в «Методике подготовки школьников к олимпиаде по информатике» Л. Д. Азиевой [10] описывает различные стратегии и методы подготовки. В исследованиях Е. Сагинтая, В. Стофова и А. Каттовой в статье «Olympiad in informatics — The journey from the domestic round to international competitions» [11] подробно описаны традиции международной олимпиады по информатике (IOI) в Европе. Авторы исследуют, что такое талант в программировании, как его распознать и развить, делятся результатами опроса учителей, а также своим опытом в подготовке и организации Олимпийских этапов. Их работа подчеркивает важность систематической подготовки и мотивации для достижения высоких результатов в программировании.
Исследовательская работа проводилась в специализированной школе-интернате «Дарын» г. Кентау. В анализе, проведенном в ходе исследования, приняли участие учащиеся 8–11 классов школы-интерната от 14 до 18 лет.
Исследование было проведено с целью определения актуальности вспомогательного средства в образовательной среде при подготовке к олимпиаде с целью определения эффективности использования возможностей цифровых технологий при подготовке к олимпиаде по информатике. В опросе было отмечено, что в целях получения достоверных и точных ответов от учащихся соблюдается конфиденциальность учащихся. Тип группировки опрошенных учащихся по возрастным признакам представлен на рисунке 1.
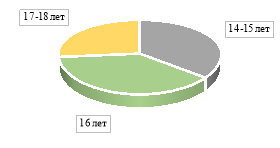
Рис. 1. Доля учащихся, принявших участие по возрастным особенностям
Как видно из рисунка 1, количество опрошенных учащихся составляет 57. Опрошенные учащиеся: 35 % — учащиеся в возрасте 14–15 лет, 39 %-учащиеся в возрасте 16 лет и 26 %-учащиеся в возрасте 17–18 лет. Мы провели опрос учащихся с 14 лет, так как у них уже сформированы базовые знания математики и логики, необходимые для освоения информатики. Эти знания способствуют успешной подготовке учащихся и высокому уровню их конкурентоспособности на международной арене. Вопросы и результаты анкетирования представлены в таблице 3 и на рисунке 2.
Таблица 3
Вопросыанкетыирезультатыанкетирования
|
№ |
Вопросы анкеты |
Да |
Нет |
Поддерживаю, потому что |
Не поддерживаю, потому что |
|
Вы участвовали в олимпиадах по информатике? |
17 |
40 | ||
|
|
Вам интересно участвовать в олимпиаде по информатике? |
50 |
7 | ||
|
|
Считаете ли вы, что участие в олимпиадах по информатике может развить вас как личность? |
55 |
2 | ||
|
|
Считаете ли вы, что участие в предметной олимпиаде полезной? |
55 |
2 | ||
|
|
Поддерживаете ли вы проведение олимпиады по информатике несколько раз в год? |
45 |
5 |
7 | |
|
|
Гарантируете ли вы, что участие в олимпиаде по информатике повысит ваши интеллектуальные способности? |
55 |
2 | ||
|
|
Поддерживаете ли вы, что на олимпиаде по информатике были задания только для программирования? |
10 |
40 |
7 | |
|
|
Мешает ли нехватка времени на подготовку к Олимпиаде недостаточная доступность цифровых технологий? |
50 |
7 | ||
|
|
Нужны ли цифровые технологии при подготовке к олимпиаде по информатике? |
50 |
1 |
6 | |
|
|
Часто ли вы используете цифровые технологии при подготовке к олимпиаде по информатике? |
50 |
7 | ||
|
|
Экономит ли использование цифровых технологий ваше время при подготовке к олимпиаде по информатике? |
55 |
2 | ||
|
|
Поддерживаю/не поддерживаю подготовку нового элективного курса в цифровой образовательной среде для подготовки к Олимпиаде |
57 |
По результатам анкетирования, всего в анкете было задано 12 вопросов, из которых были заданы вопросы поддержки и отсутствия поддержки в связи с необходимостью подготовки к олимпиаде по информатике. Как мы видим в таблице 3, большинство учащихся выразили поддержку и отметили, что особой причиной является меньшее количество элективных курсов, созданных в нашей стране, отсутствие родного языка, бесплатная и простая в использовании оцифрованная образовательная среда.
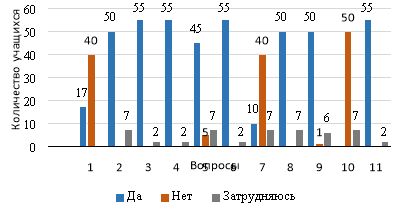
Рис. 2. Результаты опроса учащихся
Программа элективного курса, организованная в рамках исследовательской работы, основана на 34 часах, состоит из III модуля. Модуль I состоит из 16 упрощенных тем в рамках школы, модуль II состоит из 8 умеренно сложных тем, модуль III состоит из 20 наиболее сложных тем. В процессе изучения каждой темы реализуются три основных раздела: теоретические занятия; практические занятия; самостоятельная работа.
На базе специализированной школы-интерната «Дарын» г. Кентау учащиеся школы готовятся к олимпиадам с помощью дополнительного курса. Курс проводится для учащихся 8–11 классов по 1 часу в неделю. Основными темами курса являются линейный и двоичный поиск, сортировка и замена данных, длинная арифметика, рекурсия, геометрия, теория графов.
При организации элективного курса в качестве вспомогательного педагогического инструмента использовалась цифровая образовательная среда «TALPYN». Создание элективного курса позволяет, с одной стороны, — экспериментировать с материалами задач, встречающихся на конкретной Олимпиаде, с другой — знакомиться с моделью онлайн-образовательной среды, предназначенной для формирования профессиональных практических навыков олимпийского уровня и образования. Также обучающимся предлагается комплекс заданий к олимпиаде по информатике, возможность ознакомления с процессом выполнения практических заданий и их эффективного решения. Таким образом, элективный курс является необходимым инструментом для закрепления знаний обучающегося при подготовке к олимпиаде по информатике. В данном курсе с помощью цифровой образовательной среды «TALPYN» учащиеся могут полностью получить не только теоретический материал, но практические навыки для решения олимпиадных задач.

Рис. 3. Цифровая образовательная среда «TALPYN»
Существует множество способов решения олимпиадных задач курса, и выбор конкретного метода зависит от самой задачи.
Первый метод решения олимпиадных задач на основе подхода, предложенного А. Оршанским [12]. Этот метод состоит из следующих этапов:
- Определить условия обучения. На этом этапе необходимо внимательно прочитать условие отчета, не пропуская ни одного слова. Неправильное толкование договора может привести к тому, что учащийся решит совсем другую проблему, а не то, что оговорено в договоре. Как правило, в договоре есть определенные данные. Данные могут быть прямо или косвенно важными данными, относящимися к ситуации. Например, основное условие может быть скрыто в формате исходных данных.
- Построение математической модели. Необходимо внимательно рассмотреть пример входных и выходных данных и понять, почему вход соответствует выходу. Это улучшит понимание этого состояния, могут появиться и новые идеи. Создание математической модели также может помочь вам придумать решение, которое работает на абстрактной виртуальной математической машине без потерь памяти, времени, диапазона переменных и точности в реальной арифметике.
- Составить общую схему решения. Схема состоит из перехода от понимания того, что нужно сделать, к пониманию того, как это сделать. Каждый учащийся Олимпиады имеет определенное представление о части программы, из которой создаются простейшие структурные единицы программы. Разные детали имеют разные особенности модификации.
- Уточнение решения. Необходимо тщательно определить, из каких частей состоит программа, какие структуры данных необходимы и т. д. На этапе уточнения следует вспомнить, как были написаны стандартные алгоритмы.
- Реализация решения. На этом этапе программа пишется четко. Используйте разные подходы: Программирование «сверху вниз», «снизу вверх», их сочетание. Первый подход применяется, когда программа имеет общий вид — тогда пишется основная часть программы, а подпрограммы не реализуются, а только координируют свой интерфейс. Подход «снизу вверх» используется, когда нужно что-то написать, но неясно, что именно, и время идет. Затем они начинают записывать то, что им нужно в любой ситуации — ввод-вывод данных, порядок сортировки и т. д. На практике часто используется комбинация двух подходов.
- Тестирование и отладка программы. После компиляции программы необходимо проверить ее правильность. Проблемы могут быть разными: неправильный знак в Формуле, недостаточный или избыточный размер массива и т. д.; В конце концов, решение может быть в корне неправильным или неэффективным. Поэтому нужно проверить программу. Первое правило тестирования-проверка программы в тесте на примере, приведенном в договоре задания. Второе правило заключается в том, что вы должны тщательно проверить, что было получено в тесте в программе.
- Отправить программу на проверку. Вы не должны забывать данные, чтобы исправить арифметику, переполнение стека, выход за пределы массива и тому подобное, включить/отключить оптимизацию и проверить. Если ответ не приходит сразу, вам не нужно ждать ответа сервера проверки. А пока вы можете написать решение второй проблемы, подумать о третьей и им подобным.
Пример решения задачи методом Н. А. Оршанского [13]:
Условие задания: Редакция газеты «Основы информатики» решила предоставить в рекламу часть одного листа размером A×B. Поскольку популярность газеты была очень высокой, фирмы N ответили немедленно и предложили редакции разместить свою рекламу на этой странице. Объявление фирмы i известно, что
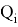
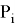
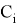
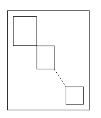
Рис. 4. Пример размещения рекламы на странице
Фирмы, если редакция согласилась, предлагали печатать свои объявления не один раз, а несколько раз, добровольно вплоть до
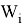
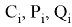
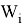
Ограничения: 2
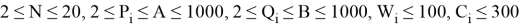
Таблица 4
Примерыдлязадания
|
Ввод |
Вывод |
|
5 55 55 14 21 10 2 7 17 15 1 12 2 35 1 9 19 23 2 19 39 45 1 |
40 |
Использует общий метод, выбранный выше, для решения этой проблемы.
Решение проблемы:
Для решения этой задачи используется метод динамического программирования с двумя ограничениями:
- Анализ задачи: необходимо определить основные идеи задачи. Задачи обратите внимание на ограничения и особенности. В этом случае классический алгоритм сумки не используется из-за двумерного характера проблемы.
- Построение математической модели: проблема динамическая с двумя ограничениями классическим примером программирования является (площадь страницы и количество развертываний). Чтобы построить модель, вы должны учитывать все возможные макеты рекламы и их пересечение, а также учитывать тот факт, что реклама не выходит за рамки страницы.
Его математическая модель:
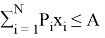
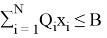
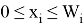
Все
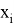
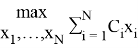
3. Составить общую схему решения. Определим последовательность функций
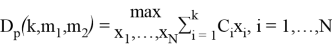
при ограничении
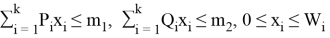
Значение
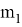
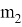
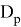
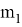
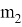
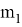
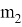
Введем разметку:
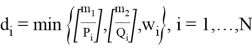
(7) первые значения функций можно найти по формуле:
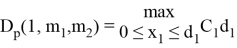
Конечно, если
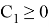
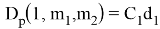
Значения функций при
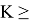
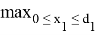
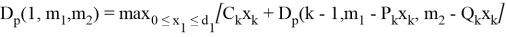
Согласно условиям этой задачи, максимальная заработная плата будет иметь значение:
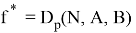
Вычислим оптимальный набор рекламных блоков:
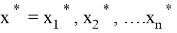
Введена функция
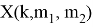
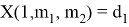
где d 1 рассчитывается по формуле (9)
При k ≥ 2 проводим расчет
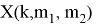
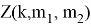
Если конкретный вариант оптимален,
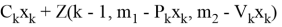
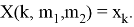
и перечислим:
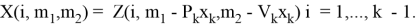
Итак, оптимальный набор рекламных блоков:
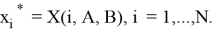
4. Приведенный выше общий метод решения имеет два существенных недостатка. Первый недостаток — это избыточный объем оперативной памяти, участвующей в решении проблемы, а второй-низкая производительность программы, реализуемой по этой схеме. Следовательно, эта схема требует оптимизации, которая заключается в:
— Функция
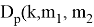
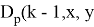
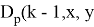
— Введем каждый условный дополнительный блок рекламы в числе 1, 2, 4 (т. е. в двух степенях) к значению, не превышающему соответствующее значение
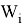
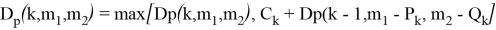
Эта задача значительно ускоряет поиск ответов, несмотря на увеличение количества не связанных блоков. Это особенно заметно, если значения A, B, W i значительно больше, чем условие.
5. Теперь осуществляем выполнение всех предыдущих пунктов общей схемы на языке C++, который является общим стандартом на всех важных олимпиадах по информатике:
#include
#include
using namespace std;
structRect {
intp; int q; int c;
Rect(int_p, int_q, int_c) {
p =_p; q =_q; c =_c;}};
vector
int pdp[1001][1001];
int main() {
int n, a, b;
cin>> n >> a >> b;
for (int i=0; i <n; <="" i++)="" p="" {=""> </n;>
int c, p, q, w;
cin>> c >> p >> q >>w;
int j=1;
while (j <w) <="" p="" {=""> </w)>
if (p*j <= a && q*j <= b) {
rects.push_back(Rect(p*j, q*j, c*j));}
w-=j;
j*=2;}
j=w;
if (p*j<=a && q*j <=b){
rects.push_back(Rect(p*j, q*j, c*j));}}
for (int it=0; it <rect.size(); ++it)="" <="" p="" {=""> </rect.size();>
for ( int i=a; i>=1; i--){
for (int j=b; j>=1; j--){
if (rects[it].p<=i && rects[it].q<=j){
dp[i][j]= max(dp[i][j], dp[i-rects[it].p][j-ects[it].q]+rects[it].c);}}}}
cout< <dp[a][b] <="" <<end1;="" p=""> </dp[a][b]>
return 0;}
6. Тестирование следует начинать с примера, приведенного в договоре задания. Для этой задачи можно придумать определенные «маленькие» тесты (таблица 5).
Таблица 5
Примерыдлязадания
|
Ввод |
Вывод |
|
2 89 16 3 8 10 5 3 6 4 5 |
12 |
|
4 401 34 5 3 7 3 5 10 5 3 8 4 2 3 3 1 1 3 |
53 |
Что касается больших текстов, лучше всего делать их только для проверки времени выполнения программы, так как будет сложно проверить правильность ответа.
7. Отправить программу на проверку. Все, что перечислено в этом пункте общей схемы, должно быть тщательно выполнено для этой задачи. Отметим, что важным моментом подготовки к олимпиадам по информатике является анализ заданий по окончании каждого соревнования, и тренерам необходимо проставить отметку в своей электронной тетради об особенностях каждого задания, отнеся его к нужной категории. Это делает систему подготовки Олимпиады легкой и удобной, с накоплением множества решенных задач.
Основная цель исследования — полная подготовка обучающихся по информатике к соревновательному уровню Олимпиады. Учащиеся развивали навыки программирования и алгоритмического мышления, готовились к олимпийским соревнованиям в результате обучения успешному решению олимпиадных заданий.
Результаты проведенной нами экспериментальной работы были оценены обучающимися с высоким, средним и низким уровнем образования.
Значение высокого уровня характеризовалось полным освоением учащимся элективного курса, разработанного для олимпиады по информатике, использованием полученных знаний, умением рассматривать пути решения сложных задач.
Значение среднего уровня характеризовалось умением обучающегося решать задачи с помощью учителя, умением самостоятельно решать задачи, овладением алгоритмом решения задач.
Значение низкого уровня характеризовалось неспособностью учащегося овладеть теоретическими, практическими данными, самостоятельно решать задачи. Сравнительный анализ усвоения обучающимися знаний, представленных на элективном курсе, представлен в таблице 6.
Таблица 6
Результатсравнительногоанализа способности обучающихся
|
Группы |
Число уч-ся |
Количество учащихся, получивших оценку |
Качество знаний |
Успеваемость | |||
|
|
|
|
| ||||
|
До эксперимента | |||||||
|
Экспериментальная группа |
|
|
|
|
|
|
|
|
Контрольная группа |
|
|
|
|
|
|
|
|
После эксперимента | |||||||
|
Экспериментальная группа |
|
|
|
|
|
|
|
|
Контрольная группа |
|
|
|
|
|
|
|
Для определения эффективности предложенных методов был проведен педагогический эксперимент, в котором приняли участие учащиеся 8–11 классов 2023–2024 учебного года. Экспериментальная группа учащихся решала олимпиадные задачи с использованием методов. Учащимся обеих групп были предложены одинаковые задания для проверки усвоения решения олимпиадных задач.
Заключение
В заключение, в школе учащиеся 8–11 классов повысили свой уровень с помощью методов и цифровой образовательной среды для решения олимпиадных задач. Применение предложенных методических подходов позволяет повысить эффективность такой подготовки учащихся к олимпиадам по информатике, а заданная задача и подход к ее решению полезны тренерам, занимающимся подготовкой учащихся к различным соревнованиям по программированию.
Литература:
- Официальный сайт Президента РК. Глава государства принял участие в республиканском съезде педагогов.– Астана. — 2023. [Электронный ресурс]: URL: https://www.akorda.kz/kz/memleket-basshysy-respublikalyk-pedagogter-sezine-katysty-595143
- Sagyntay Y., Stoffovа V., Katyetova A. Оlympiad in informatics — the journey from the domestic round to international competition // ICERI — 2023. 16th International Conference of Education, Research and Innovation. — 13–15 November 2023. — Spain: IATED Academy. 2023. — p. 5192–5198.
- Сеничева Н.Н, Соколова Д. В. Участие в конкурсах и олимпиадах как форма развития одаренности обучающихся // Вопросы территориального развития. — 2015. — № 9 (29). — 5 p.
- Результаты международной олимпиады по информатике. [Электронный ресурс]: URL: https://scoreboard.bc-pf.org/results/informatics/international-olympiad-in-informatics
- Результаты Международной Жаутыковской олимпиады. [Электронный ресурс]: URL: https://scoreboard.bc-pf.org/kk/results/informatics/international-zhautykov-olympiad
- Об утверждении государственных общеобязательных стандартов дошкольного воспитания и обучения, начального, основного среднего, общего среднего, технического и профессионального, послесреднего образования // Приказ Министра образования и науки Республики Казахстан от 3 августа 2022 года № 348. Зарегистрирован в Министерстве юстиции Республики Казахстан 5 августа 2022 года № 29031.
- Павлова Е. С. Методика использования систем задач как средства развития одаренности при подготовке школьников к олимпиадам по информатике. Автореферат диссертации... доктора педагогических наук. — Волгоград. — 2016. — 26 с.
- Чудова Н. В., Долныкова А. А. Научная дискуссия: вопросы педагогики и психологии // Сборник статей по материалам XLV международной заочной научно-практической конференции. — Москва. — № 12 (45). — Декабрь 2015 г. — 152 с.
- Овсянников В. И. Дистанционное образование в России: постановка проблемы и опыт организации: учеб. пос./ Овсянников В. И., Кашицин В. П. — М.: РИЦ «Альфа» МГОПУ им. М. А. Шолохова. — 2015. — 794 с.
- Азиева Л. Д. (2018). Методика подготовки школьников к олимпиаде по информатике. Мир науки, культуры, образования, (3 (70)), 315–317.
- Sagyntay, Yerkebulan & Stoffova, Veronika & Katyetova, Aliya. (2023). Olympiad in informatics — the journey from the domestic round to international competitions. 5192–5198. 10.21125/iceri.2023.1299.
- Авдеюк О. А., Дружинина Л. В., Лемешкина И. Г., Павлова Е. С., Приходькова И. В., Королева И. Ю. Проблемы и методы их решения при подготовке школьников к участию в олимпиадах по информатике// Современные наукоемкие технологии. — 2017. — № 4. — С. 60–64
- Оршанский С. А. О решении олимпиадных задач по программированию формата ACMICPC // Мир ПК — Диск. — 2005. № 9. — 30 c.