Для проведения моделирования поведения звена с использованием разработанного ПК, необходимо представить его реализацию в системе моделирования, определить начальные данные и провести анализ полученных результатов. В качестве результатов моделирования могут выступать как табличные значения, так и графики изменения маркировки сети.
В ТАУ в качестве входных воздействий, на которые ищется реакция звена, приняты воздействия, описываемые элементарными математическими функциями, то есть такими, на которые можно разложить любые произвольные функции.
Модель безынерционного звена.
В качестве начальных данных для анализа правильности представленной структуры звена и работы аппарата будем использовать единичную ступенчатую функцию l(t) и произвольный сигнал, величина которого равномерно убывает в течение времени.
На рисунке 1 представлена реализация звена с использованием программного комплекса. Безынерционное звено представлено непрерывной позицией H1, дискретной позицией Д1 и переходом квантования К1. Дуга, соединяющая переход квантования К1 и дискретную позицию Д1, имеет вес 2, что соответствует коэффициенту пропорциональности звена.
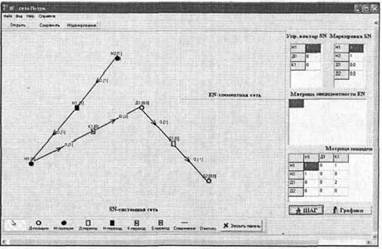
Рис. 1. Моделирование поведения безынерционного звена
Для реализации единичной ступенчатой функции необходимо в непрерывную позицию HI, с начальной маркировкой равной 0, подать непрерывный сигнал равный 1, и поддерживать его в течение последующего времени моделирования. Для чего воспользуемся непрерывной позицией Н2, с начальной маркировкой равной 1, и непрерывным переходом H1, с пропускной способностью равной 1.
При наличии единичного сигнала на входе звена, переход квантования будет каждый шаг моделирования передавать на выход новые значения, которые в свою очередь будут там накапливаться, поэтому реализуем вспомогательную «ветвь» сети Петри. Она представлена дискретным переходом Д1 и дискретной позицией Д2. Основная задача их в освобождении дискретной позиции Д1, что достигается весом дуги, соединяющей дискретный переход Д1 и дискретную позицию Д2, равным -1. Снимаемые переходом квантования значения будут накапливаться в позиции Д2, а в Д1 все время будет формироваться новое значение квантования.
Таблица 1
Результаты моделирования поведения безынерционного звена
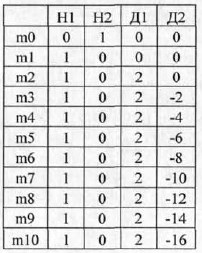
Следует отметить, что результат на выходе звена появляется с задержкой в один временной интервал. Значения, полученные при моделировании полностью совпадают с теоретически полученными.
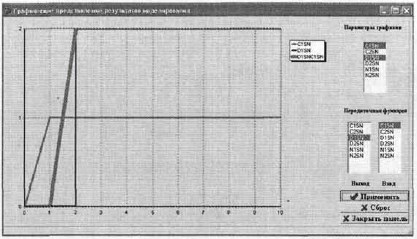
Рис. 2. Графики изменения маркировки позиций
Рассмотрим второй случай. Если на вход звена подается произвольный сигнал, величина которого равномерно убывает в течение времени. Реализация звена представлена на рисунке 3. Рисунок аналогичен представленному выше лишь с тем отличием, что изначально в непрерывной позиции H1 сформирован сигнал, уровень которого с течением времени уменьшается. Кроме того, коэффициент пропорциональности звена в этом случае равен 1.
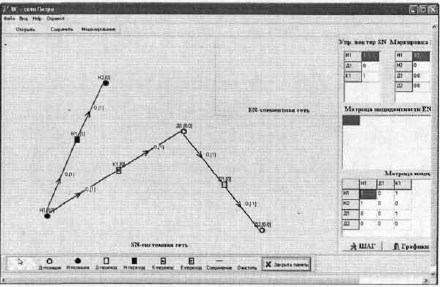
Рис. 3. Моделирование поведения безынерционного звена
Результаты моделирования представлены в таблице 2 и на рисунке 4. Отметим, что результат на выходе звена появляется также с задержкой в один временной интервал. Значения, полученные при моделировании полностью совпадают с теоретически полученными.
Таблица 2
Результаты моделирования поведения безынерционного звена
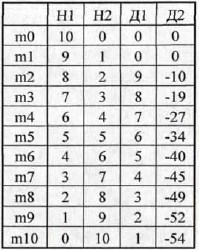
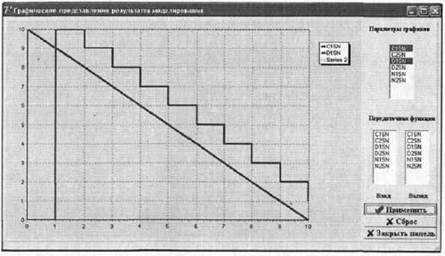
Рис. 4. Графики изменения маркировки позиций
Из анализа результатов моделирования можно сделать вывод об адекватности представленной модели безынерционному звену.
Модель идеального дифференцирующего звена.
В качестве начальных данных для анализа правильности представленной структуры звена и работы аппарата будем использовать произвольный сигнал, величина которого равномерно увеличивается в течение времени.
Реализация идеального дифференцирующего звена с использованием разработанного комплекса представлена на рисунке 5.
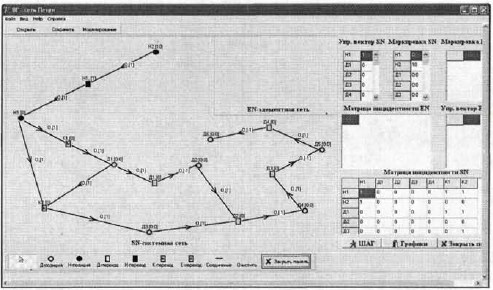
Рис. 5. Моделирование поведения идеального дифференцирующего звена
Идеально дифференцирующего звено представлено непрерывной позицией H1, дискретными позициями Д1-Д5, дискретными переходами Д1-ДЗ и переходами квантования К1, К2. Непрерывная позиция H1 является входом звена, а дискретная Д5 — выходом. Связка непрерывного перехода H1 и непрерывной позиции Н2 служат источником повышения сигнала в позиции H1. Дискретные переход Д4 и позиция Д6 необходимы для накопления результатов работы звена.
Результаты моделирования представлены в таблице 3, рисунках 6 и 7. Следует отметить, что результат на выходе звена появляется с задержкой в пять временных интервалов. Значения, полученные при моделировании полностью совпадают с теоретически полученными.
Таблица 3
Результаты моделирования идеального дифференцирующего звена
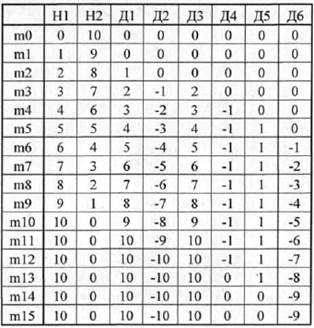
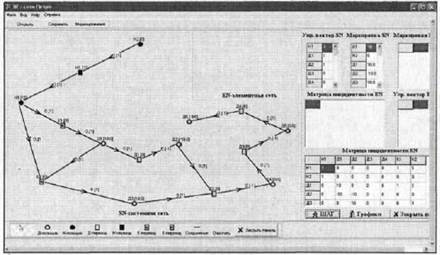
Рис. 6. Результаты моделирования после 15 шагов
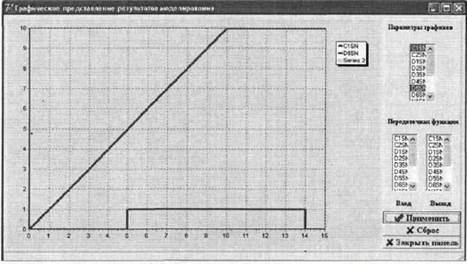
Рис. 7. Графики изменения маркировки позиций
Из анализа результатов моделирования можно сделать вывод об адекватности представленной модели идеальному дифференцирующему звену.
Модель идеального интегрирующего звена.
В качестве начальных данных для анализа правильности представленной структуры звена и работы аппарата будем использовать произвольный сигнал, величина которого равномерно уменьшается в течение времени.
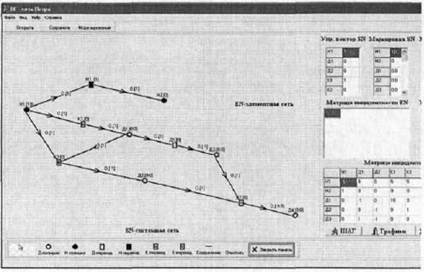
Рис. 8. Моделирование поведения идеального интегрирующего звена
Реализация идеального интегрирующего звена с использованием разработанного комплекса представлена на рисунке 8.
Идеально интегрирующее звено представлено непрерывной позицией H1, множеством дискретных позиций Д1-Д4, переходами квантования К1-К4, дискретными переходами Д1, Д2. Непрерывный переход H1 и непрерывная позиция Н2 обеспечивают изменение сигнала в позиции H1 во времени.
Результаты моделирования представлены в таблице 4, рисунках. Следует отметить, что результат на выходе звена появляется с задержкой в три временных интервала. Средняя ошибка вычисления составила 2,5 %.
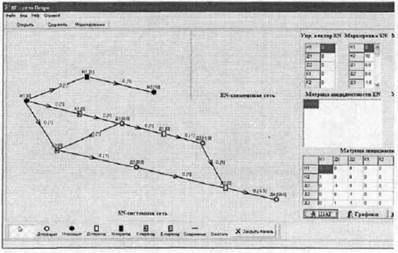
Рис. 9. Результаты моделирования после 12 шагов
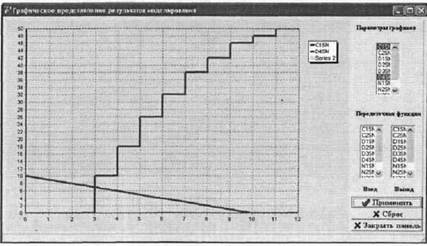
Рис. 10. Графики изменения маркировки сети
Из анализа результатов моделирования можно сделать вывод об адекватности представленной модели идеальному интегрирующему звену.
Так как программный комплекс (ПК) в целом представляет собой довольно большой код, объединяющий несколько подпрограмм, в данной статье были рассмотрены только несколько алгоритмов.
Разработка ПК велась на языке Delphi 7.0. Данный язык программирования обладает широкими возможностями по созданию приложений для среды Windows. Являясь объектно-ориентированным языком программирования, Delphi позволяет значительно сократить затраты на реализацию программного кода приложения.
В ходе работы над ПК были разработаны классы позиций TPosition, переходов ТРег, дуг TDuga и графических элементов TOblm. При разработке класса дуг был разработан новый компонент Line. Разработка данного компонента оказалась необходимой вследствие того, что в среде Delphi нет компонента, позволяющего соединить два графических изображения простой линией, таким образом, чтобы к созданной линии можно было бы обращаться как к объекту, последнее должно упростить ряд операций над линиями (дугами сети Петри).

Рис. 11. Пример программной реализации процедуры вычисления маркировки ГСП
Построенное ПО наглядно отображает результаты моделирования. Кроме того, программный комплекс позволяет оперативно вмешиваться в процесс моделирования при обнаружении ошибок и недочетов в исходной модели.
В терминах модифицированного аппарата сетей Петри разработаны и промоделированы минимально необходимые типовые динамические звенья. Реализованная на основе программного комплекса библиотека типовых динамических звеньев позволяет строить системы любой сложности в терминах сетей Петри, опираясь на правила и законы ТАУ.
Литература:
1. Баженова И. Ю. Delphi 7. Самоучитель программиста. — M.: Кудиц — образ, 2003. -448с.
2. Бусленко Н. П. Моделирование сложных систем. — М.: Наука, 1978. — 400с.
3. Давыдов Д. В. Методы и модели анализа сетей АСУ с поддержкой качества обслуживания. — Вологда: ВоГТУ, 2007. — 139 с.
4. Культин Н. Б. Основы программирования в Delphi 7. — СПб.: БХВ — Петербург, 2003. — 608 с.
5. Куо Б. Теория и проектирование цифровых систем управления, перевод с английского. — М.: Машиностроение, 1986. — 446с.
6. Питерсон Дж. Теория сетей Петри и моделирование систем. — М.: Мир, 1984.-264с.







