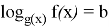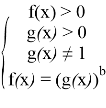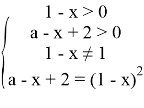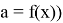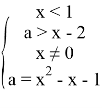В статье рассматривается один из приемов конструирования идей решения заданий с параметрами в содержании Единого государственного экзамена.
Ключевые слова: идея решения, задание с параметром, приемы конструирования идеи решения, Единый государственный экзамен.
Сдача Единого государственного экзамена является неотъемлемой частью завершения обучения школьников. Одним из самых трудных заданий в содержании профильной математики является 17-е задание — задание с параметром. Данные задания вызывают затруднения как у учащихся (выбор способа решения), так и у учителей (недостаточность методических материалов в структурировании теории данной темы). Сконструировать идеи, которые могут помочь учащимся по условию задания определять к какому типу и каким методом решать задание, включающее в себя параметр, является значимым и актуальным.
Под идеей решения будем понимать «мысль, направляющую на план по внешнему виду». [3]
Существуют различные приемы для конструирования идей решения задания. Рассмотрим некоторые из них, которые, на наш взгляд, целесообразны в решении заданий с параметрами:
- Формулирование поисковых вопросов по условию задания (основывается на базовой методике работы с алгебраическим заданием, одним их этапов которой является этап поиска путей решения, который обязательно должен заканчиваться планом решения [5]).
- Прием перефразирования условия задания (основывается на замене условия (заключения, условия и заключения) на новое заключение (условие, условие и заключение), что позволяет рассматривать получившуюся конструкцию с позиции более знакомых для учащихся математических фактов [6]).
- Прием аналогии (основывается на сведении к решению некоторой известной вспомогательной задачи и переносе хода рассуждений на исходную [2]).
- Прием классификации заданий (основывается на выделении группы заданий, решаемых единым методом, или группы заданий, сходных по единой конструкции [1]).
Учитывая специфику заданий с параметрами, а именно их принадлежность к той или иной математической теме (квадратное неравенство с параметром, тригонометрическое уравнение с параметром и т. д.), что позволяет говорить о приеме классификации для конструирования идей их решения, определим направления успешной подготовки учащихся к их решению на Едином государственном экзамене:
- Включать задания с параметром необходимо на всех этапах обучения, начиная с седьмого класса (например, линейные уравнения с параметром целесообразно изучать в теме линейные уравнения).
- Конструировать идею решения задания с параметром возможно по условию задания (не обращая внимания на параметр), отнеся уравнение или неравенство к известному виду, а следовательно, и способу решения.
Таким образом, для решения заданий с параметрами в содержании ЕГЭ учащийся должен уметь отнести уравнение (неравенство) к известному классу, не обращая внимания на параметр, и владеть математическими основами решения, соответствующего уравнений данного класса [3].
В нашем исследовании прием конструирования идей решения задания с параметром по его условию, основанного на вышеуказанных умениях и владениях, реализуется через систему установок: ««Я вижу…»; «Я знаю, что …», «Я могу …» .
Рассмотрим задание с параметром [4]:
Найдите все значения а, для каждого из которых уравнение
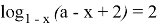
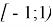
Анализ условия начинают с того, что учащиеся, не обращая внимание на параметр, начинают анализировать условие и отвечают на поставленные вопросы на основе имеющихся знаний из школьного курса. В последствии такой анализ выводит на план решения заданий с параметрами.
|
1 |
Я ВИЖУ… Какое уравнение представлено в условии, если не обращать внимание на параметр? |
Логарифмическое уравнение вида
|
|
2 |
Я ЗНАЮ, ЧТО уравнение такого вида решается по схеме |
|
|
3 |
Я МОГУ реализовать эту схему для данного уравнения |
|
|
4 |
Я ВИЖУ
, что в каждом уравнении и неравенстве системы параметр
а
«легко» выражается через
х
(можно задать элементарные функции вида
|
|
|
5 |
Я МОГУ сформулировать план решения: |
1)Изобразить графики уравнений и неравенств в системе хОа; 2) Нанести числовой промежуток из условия; 3) Смоделировать ситуацию согласно условию задачи; 4) Ответить на вопрос задачи; 5) Записать ответ |
Таким образом, использование приема «Я вижу»...является целесообразным в конструировании идеи решения заданий с параметрами.
Литература:
- Малинникова Н. А., Александрович А. Л. Комплексы заданий с параметрами: подготовка к ЕГЭ. Ученые записки Брянского государственного университета. — Брянск, 2019, № 2, С. 16–24
- Малинникова Н. А., Бушуева Е. А. Еще раз об алгоритмах в заданиях с параметром. Перспективные научные исследования: опыт, проблемы и перспективы развития / Сборник научных статей по материалам V Международной научно-практической конференции (25.06.2021 г., г.Уфа) / — Уфа: Изд. НИЦ Вестник науки, 2021. С. 9–13
- Малинникова Н. А. О конструировании идей решения заданий с и параметрами. Материалы 41-го Международного научного семинара преподавателей математики и информатики университетов и педагогических вузов. — Киров, 2022. С. 234–235
- Малова И. Е. Теория и методика обучения математике в средней школе: учеб. пособие для студентов вузов/ И. Е. Малова [и др.]- М.: Гуманитар. изд. центр Владос, 2009. — 445 с.
- Сайт Решу ЕГЭ. [Электронный ресурс]. URL: https://math-ege.sdamgia.ru/
- Яцковская Г. А. Математические затруднения учащихся, связанные с нахождением области значений функции, и методические пути их преодоления. Подготовка учащихся к ЕГЭ-2010 по математике: математические затруднения учащихся и методические пути их преодоления: Пособие для учителей математики учреждений среднего и профессионального образования Брянской области. — Выпуск 3. — Брянск: РИО БГУ, 2010. — С.6–71.