В настоящей статье рассматривается актуальность использования межпредметных связей «математика-физика», определяются темы школьного курса, содержащие вышеуказанные связи. Рассматриваются существующие проблемы реализации межпредметных связей, предлагаются пути их решения. Приведены примеры заданий, содержащие межпредметные связи.
Ключевые слова: математика, физика, межпредметные связи.
В настоящее время в Федеральном государственном образовательном стандарте основного общего образования (далее — ФГОС ООО) на государственном уровне определена цель: воспитание творческой, свободной личности, исповедующей ценности демократического общества [1]. Перед школой ставятся задачи выявления и развития способностей каждого ученика, достижение им не только предметных, но и метапредметных и личностных результатов. Стандарт ориентирует педагогов на формирование у ученика ключевых компетенций, которые обеспечат ему гибкость и адаптивность по отношению к быстро изменяющемуся миру, то есть не только на предметные результаты, как это было раньше, но и на метапредметные. Метапредметные результаты включают освоение учащимися межпредметных понятий [3].
Однако существует ряд проблем достижения метапредметных образовательных результатов. Среди наиболее важных отметим недостаточность соответствующих учебников, методической литературы. Достижение метапредметных результатов требует дополнительных усилий учителей-предметников, в частности, знания материала других предметов; необходимо объединение усилий всех учителей-предметников, работающих в определённом классе. Методика формирования межпредметных понятий и подчинённых им понятий должна включать как общую, универсальную часть для разных учебных предметов, так и специфичную для каждого учебного предмета.
Изучение всех предметов естественнонаучного цикла тесно связано с математикой. Сущность развития ученика путем изучения математики состоит в формировании у обучающихся единства разных видов знаний и умений — специфически математических и общеинтеллектуальных, реализуемых на математическом материале. Полноценное обучение математике невозможно без понимания детьми происхождения и значимости математических понятий, роли математики в системе наук. Этот предмет дает учащимся систему знаний и умений, необходимых в повседневной жизни и трудовой деятельности человека, а также для изучения смежных предметов. Одним из наиболее важных таких предметов является физика.
Математика помогает физике устанавливать и описывать законы окружающей среды. Физика делится с математикой реальностью изучаемых процессов и объектов, моделирует естественным образом отрицательные числа, пропорции, векторы и многое другое. Наблюдая за реальными физическими процессами, ученики осознают, что силы образуют пары, как и противоположные по знакам числа; знакомятся с понятием рычага, а в дальнейшем узнают, как оно связано с пропорцией и средними значениями величин [4].
Преемственные связи математики с курсом физики раскрывают практическое применение математических умений и навыков. Это способствует формированию у учащихся целостного научного мировоззрения. Главной задачей педагога представляется демонстрация учащимся единства и дополнения различных подходов, а не проведение какого-либо их сравнительного анализа.
Математический аппарат необходим физике как язык для описания физических процессов и явлений, один из методов физического исследования.
Рассмотрим рабочие программы [5, 6] и содержание учебных предметов математика и физика основного общего образования [2] за 7 класс (таблица 1).
Таблица 1
Содержание учебного предмета
|
Содержание учебного предмета | ||
|
Физика. 7 класс |
Математика. 7 класс | |
|
Геометрия |
Алгебра | |
|
Физика и физические методы изучения природы. Строение и свойства вещества. Взаимодействия тел. Давления твёрдых тел, жидкостей и газов. Работа и мощность. Энергия |
Простейшие геометрические фигуры и их свойства. Треугольники. Параллельные прямые. Сумма углов треугольника. Окружность и круг. Геометрические построения |
Линейные уравнения с одной переменной. Целые выражения. Функции. Системы линейных уравнений с двумя переменными |
Первая тема, в которой появляются элементы межпредметных связей это «Измерение величин». В математике первое знакомство со шкалой и единичным отрезком (ценой деления) начинается в пятом классе. В качестве примеров рассматриваются линейка, циферблат, спидометр, комнатный термометр, весы, транспортир. Вводятся определения «единичный отрезок» и «длинна отрезка», а так же различные единицы длины, например: 1 мм, 1 дм, 1 км и т. д. Продолжение данной темы можно встретить в курсе геометрии седьмого класса в темах «Отрезок и его длина» и «Измерение углов». Здесь в качестве примеров рассматриваются уже более сложные измерительные приборы: штангенциркуль, микрометр, полевой циркуль, астролябия — для измерения горизонтальных углов и определения широт и долгот небесных тел; теодолит — для измерения местности, буссоль — в артиллерии; секстант — в мореплавании.
В физике данная тема впервые появляется в седьмом классе: «Физические величины. Измерение физических величин». Здесь даётся определение измерению величин с физической точки и вводится понятие «Международной системы единиц — СИ (система интернациональная)». В качестве примеров приводятся уже физические измерительные приборы: измерительный цилиндр, амперметр, вольтметр, секундомеры, термометры, электронные весы, шагомеры.
Следующая тема — «Погрешности измерений». В математике эта тема изучается в пятом классе «Округление чисел. Прикидки». Здесь вводится понятие округления чисел и приближённого значения, и даются правила округления натуральных чисел и десятичных дробей. Далее тема погрешностей встретится учащимся в курсе алгебры за девятый класс «Абсолютная и относительная погрешности», где будут введены определения «абсолютной и относительной погрешности» и приводятся формулы абсолютной погрешности:
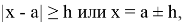
и относительной погрешности:
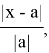
где
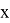
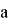
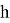
В физике тема «Точность и погрешность измерений» рассматривается в седьмом классе. Здесь же вводится понятие «погрешности» и приводится формула записи величин с учётом погрешности:
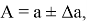
где
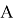
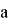
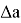

Можно заметить, что формулы погрешности в математике и физике различаются только обозначением, при этом их смысл сохраняется.
Третья тема, где есть преемственные связи математики с курсом физики — «Движение». В математике задачи на движение изучаются в начальной школе. Вводится понятие «скорость», «время», «расстояние» и показывается зависимость этих величин. Для изучения зависимости одной величины от другой в шестом классе изучается тема «Отношения и пропорции». Вводятся понятия «отношение числа
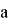
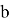
В физике изучается взаимодействие тел. Появляются понятия «путь», «траектория», «равномерное и неравномерное движения». Здесь учащиеся седьмого класса для решения задач по темам «Движение», «Сила упругости», «Изменение агрегатных состояний вещества», «Перемещение при прямолинейном равномерном движении», «Перемещение при прямолинейном равноускоренном движении» могут применить свои знания из курса математики за шестой класс, используя графики зависимости.
Следующая тема с элементами межпредметных связей — «Масса и объём». При изучении темы «Объём» в курсе математики пятого класса у учащихся формируется представление об объёмных геометрических фигурах. Вводятся понятия «измерение объёма» и «свойства объёмной фигуры». Учащиеся знакомятся понятием «единичный куб».
В физике для нахождения массы необходимо знать объём. Учащиеся седьмого класса узнают новую формулу для нахождения объёма:
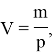
где
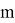
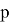
В теме «Центр тяжести. Условия равновесия тел» в физике можно увидеть сходство с темой геометрии «Метод масс». В геометрии центром масс называют такую точку
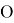
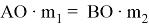
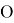
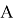
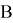
Таким образом, учебный процесс требует использования межпредметных связей физики и математики, а именно сочетания теоретических методов изучения физики с экспериментальными методами на основе доступных понятий элементарной математики. Этот подход обеспечивает одновременно достижение высокого уровня усвоения математики, формирует критическое и логическое мышление учеников, а также способствует пониманию единства материального мира. У учащихся появляется понимание того, что математические формулы и уравнения реально воплощаются в жизнь в физических процессах.
Литература:
- Федеральный государственный образовательный стандарт основного общего образования. URL: https://fgos.ru/fgos/fgos-ooo/ (дата обращения: 29.03.2023).
- Приказ Министерства просвещения Российской Федерации от 16.11.2022 № 993 «Об утверждении федеральной образовательной программы основного общего образования» (Зарегистрирован 22.12.2022 № 71764) URL: https://edsoo.ru/Federalnaya_obrazovatelnaya_programma _osnovnogo_obschego_obrazovaniya.htm (дата обращения 29.03.2023).
- Подходова Н. С. Метаметодическая модель школы (в контексте образовательных стандартов второго поколения) // Письма в Эмиссия. Оффлайн. 2010.
- Кожекина Т. В., Никифоров Г. Г. Пути реализации связи с математикой в преподавании физики // Физика в школе. 1982. № 3. С. 38.
- Математика: рабочие программы : 5-11 класс / сост. А. Г. Мерзляк, В. Б. Полонский. М. С. Якир, Е. В. Буцко. – 3 изд., перераб. – Москва : Вента-Граф, 2020 – 164 с.
- Физика: рабочие программы : 7-9 класс / сост. А. В. Перышкин, Н. В. Филонович, Е. М. Гутник. – из сб. Физика. 7-9 классы : рабочие программы / сост. Е. Н. Тихонова. – 5-е изд., перераб. – М. : Дрофа, 2015. – 400 с.

