В статье приведен обзор математических подходов моделирования транспортных потоков, рассмотрена модель и пример задачи многопериодного потока (динамической сети).
Введение
Динамика городского населения имеет устойчивую тенденцию к росту. Вместе с ростом городских агломерацией увеличивается количество транспортных единиц пассажирского, грузового и личного транспорта. Согласно статистике, в крупных городах доля личного транспорта составляет более 50 % и имеет тренд к увеличению, что в свою очередь неизбежно приводит к увеличению транспортных потоков и к проблемам управления ими. При моделировании управления транспортными потоками широко используют математический аппарат, например:
- Теорию графов
- Теорию очередей
- Имитационное моделирование
- Теорию случайных процессов
- Модели случайных графов
- Дифференциальные модели (транспортный поток как гидродинамическая аналогия)
- Нейронные сети («умный» режим работы системы светофоров) и многое другое.
Методы моделирования транспортных потоков комбинируются, постоянно дополняются и совершенствуются.
Мы рассмотрим математическую модель и пример задачи многопериодного потока (динамической сети).
1. Математическая модель многопериодного потока
В многопериодных потоках может потребоваться несколько периодов для переноса потока по сети (например, в модели сети трубопровода, решение может интерпретироваться как поток, который происходит в течение одного периода и затем останавливается).
Для алгебраического представления динамической сети мы должны определить:
Параметры:
L ( i,j ) = время выполнения, в периоде, для прохождения потока из узла i к узлу j по дуге от i до j ,
Переменные:
xijt = поток, входящий в дугу ij в уле i в период t , и поэтому выходящий в j в период t+L ( i, j ),
Vjt = запас, остающийся в узле j в конце периода t ,
Основное уравнение баланса узла говорит, что (запас в узле k в конце периода t ) = (конечный запас в k в предшествующий период) + (прибывающие потоки) — (потоки из k в t ), или алгебраически:
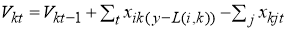
2. Пример задачи многопериодного потока
На рис.1 представлен пример. Вершины графа (узлы) являются узкими местами (перекресток со светофором), где может собраться транспорт. Ребра графа (дуги) соответствуют дорогам. Число транспортных единиц, которые покинут каждый узел за период, обозначено красным шрифтом под каждым узлом. Периодом является 10-минутный интервал. Число, которое ниже каждой дуги, является числом периодов, которые он допускает для прохождения по дуге. Цифра выше каждой дуги, является верхним пропускным пределом транспортных единиц через дугу за период. Число, появляющееся выше каждого узла, является верхним пределом единиц транспорта, которые могут ожидать в узле. Узел F соответствует выходу. Необходимо минимизировать количество периодов, которое требуется для освобождения всех узлов.
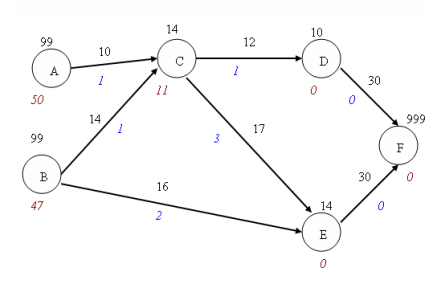
Рис. 1. Граф примера задачи многопериодного потока
Решение данной модели было реализовано в оптимизационном пакете Lingo. Результат данной задачи — 70 минут, т. е. за 7 интервалов поток полностью пройдет данный участок пути.
Выводы
В реальных транспортных системах нас чаще интересует поток, который варьируется от периода до периода (а не как стационарное состояние или как задача непрерывного потока (потока одного периода)), т. е. мы интересуемся многопериодными или динамическими решениями. Рассмотренная модель является примером динамического потока и может использоваться как элемент при моделировании сложной системы транспортных потоков.
Литература:
- Введение в математическое моделирование транспортных потоков: учеб. пособие / Гасников А. В., Кленов С. Л., Нурминский Е. А., Холодов Я. А., Шамрай Н. Б.; Приложения: Бланк М. Л., Гасникова Е. В., Замятин А. А. и Малышев В. А., Колесников А. В., Райгородский А.М; Под ред. А. В. Гасникова. — М.: МФТИ, 2010. — 362 с..
- Симонов, Б. В. Элементы теории графов. Теория и практика: учеб. пособие / Б. В. Симонов, О. А. Авдеюк, И. Э. Симонова, И. А. Тарасова; ВолгГТУ. — Волгоград, 2014. — 80 с.
- Linus Shrage. Optimization Modeling with LINGO. Sixth Edition. — Режим доступа: www. Lindo.com.
- Оптимизация в инженерных и управленческих задачах: учеб. пособ.(гриф). Доп. Федеральным УМО по укрупнённой группе специальностей и направлений подготовки 23.00.00 «Техника и технологии наземного транспорта» / В. М. Волчков, А. Е. Годенко, Я. В. Калинин, И. А. Тарасова; ВолгГТУ. — Волгоград, 2018. — 134 с.
- Моделирование узких мест (перекрестков со светофорами) транспортных потоков. Подсеваткин Г. С. В книге: Конкурс научно-исследовательских работ студентов Волгоградского государственного технического университета. Тезисы докладов. Волгоград, 2021.







