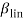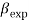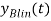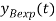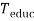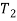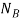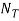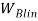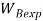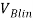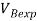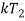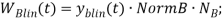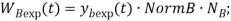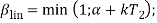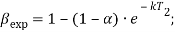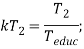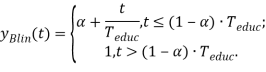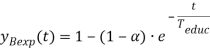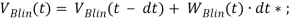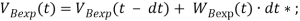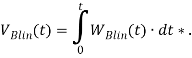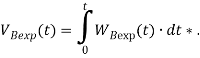В процессе обучения школьники должны выполнить некоторый запланированный объем работ (прослушать материал, разобраться в нем, выполнять домашние задания, писать проверочные работы и т. д.), который выполняется имеющимся количеством учеников за конечное время. Поскольку уровень подготовки и природные данные учеников отличаются, возникает ситуация, когда более грамотные ученики готовы изучать новый материал, а менее способным необходимо проведение дополнительных занятий. У преподавателя возникает непростая задача: проанализировать сложившуюся ситуацию и сделать выбор, что будет лучше в целом для итоговой общей успеваемости учеников. Имитационное моделирование позволит проанализировать разные случаи и сделать вывод, как лучше поступить в той или иной сложившейся ситуации.
In the learning process, students must complete a certain planned amount of work (listen to the material, understand it, do homework, write test papers, etc.), which is performed by the available number of students in a finite time. Since the level of training of students and natural data for all students are different, a situation arises when more literate students are ready to learn new material, and less capable students need to conduct additional classes. The teacher has a difficult task: to analyze the current situation and make a choice, which will be better overall for the final overall performance of students. Simulation modeling will allow you to analyze different cases and draw a conclusion on how best to act in a given situation.
В рамках данной статьи в разработанной имитационной модели будут использованы 2 модели обучения:
— линейная;
— экспоненциальная.
Отстающих учеников обозначим как «новичков», успевающих как «профессионалов».
Линейная модель подходит для описания обучения человека, который будет выполнять много чисто механической работы, например, решать однотипные задачи до тех пор, пока количество не перейдет в качество.
Экспоненциальная модель больше подходит для описания обучения человека, который будет реализовывать более нетривиальные задачи, сможет принимать решения самостоятельно, запоминать разные способы решения задач и прочее.
Экспоненциальная модель обучения наиболее близка к реальности, чем линейная, так как при подготовке к экзаменам ученики, так или иначе сталкиваются с ситуациями, когда необходимо самостоятельно выбирать методы решения сложных задач.
Одним из основных параметров моделей обучения является время обучения новичков. Для того, чтобы использовать эти модели обучения необходимо знать, как время обучения зависит от количества обучающих и обучаемых. Эта зависимость описывается моделью времени группового обучения.
Модель времени группового обучения показывает, как результирующее время обучения зависит от индивидуального и общего (группового). Общее время обучения — время, которое тратится на общее количество обучаемых. Независимо от количества обучающих и обучаемых это время не изменяется. Индивидуальное время обучения — время которое необходимо для индивидуального обучения каждого из новичков. Это время уменьшается при увеличении количества обучающих. Однако, данный эффект сохраняется до тех пор, пока число обучающих не превысит число обучаемых.
Основным параметром в обеих моделях обучения является уровень обученности новичков. Под уровнем обученности понимается соответствие текущей производительности ученика установленной норме. Естественно, каждый новичок обладает начальным уровнем обученности. Предполагается, что начальный уровень обученности всех новичков одинаков.
При использовании линейной модели обучения производительность новичков вырастает за единицу времени на какую-то постоянную. График, который показывает зависимость уровня обученности от времени в линейной модели, приведен на рисунке 1. Сплошная линия показывает динамику уровня обучаемости под руководством профессионалов, которая прекращается в некоторый момент времени. Новичок при этом достигает некоторого уровня, с которым он продолжает работать дальше. Пунктирная линия отражает динамику уровня обученности в предположении, что новичок продолжает обучаться самостоятельно.
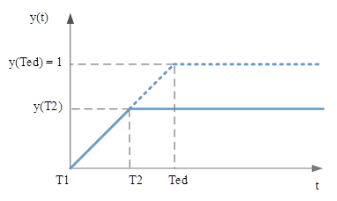
Рис. 1. Линейная модель обучения
При использовании экспоненциальной модели обучения производительность новичков за единицу времени увеличивается не на постоянную величину, а пропорционально отклонению производительности от идеала. На рисунке 2 представлена зависимость уровня обученности от времени в экспоненциальной модели обучения. Аналогично рисунку 1 пунктирная линия описывает случай, когда новички продолжают обучаться самостоятельно.
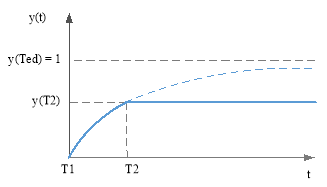
Рис. 2. Экспоненциальная модель обучения новичка
Для составления имитационных моделей обучения исследуемой системы, составлен список всех параметров и характеристик системы. Обозначение, описание и единицы измерения данных параметров указаны в таблице 1.
Таблица 1
Переменные для формализации моделей обучения
|
Обозначение |
Описание |
Единица измерения |
|
α |
Коэффициент, обозначающий начальный уровень обученности новичка. |
Безразмерная величина. Принимает значение от 0 до 1 включительно |
|
|
Коэффициент, обозначающий уровень обученности новичка к концу времени обучения профессионалами вычисленный при помощи линейной/ экспоненциальной модели обучения |
Безразмерная величина. Принимает значение от 0 до 1 |
|
|
Коэффициент, обозначающий текущий уровень обученности новичка в случае использования линейной/ экспоненциальной модели |
Безразмерная величина. Принимает значение от 0 до 1 включительно |
|
|
Время обучения новичков |
День |
|
|
Время обучения группы новичков группой профессионалов |
День |
|
t |
Время, прошедшее с начала обучения |
День |
|
|
Количество новичков |
Шт. |
|
|
Количество профессионалов, выделенных на обучение |
Шт. |
|
NormB |
Норма для новичка |
Строки/день |
|
|
Текущая производительность новичков, при использовании линейной/ экспоненциальной модели обучения |
Задачи/день |
|
|
Текущий объем работы, выполненный новичками, при использовании линейной/ экспоненциальной модели обучения |
Задачи |
|
|
Коэффициент, описывающий отношение времени обучения с профессионалами ко времени, необходимому для полного обучения |
Безразмерная величина. Принимает значение от 0 до 1 включительно |
Графические диаграммы причинных связей (согласно терминологии системной динамики), разработанные с использованием пакета для имитационного моделирования iThink [1–3], для линейной и экспоненциальной моделей обучения предоставлены на рисунке 3.
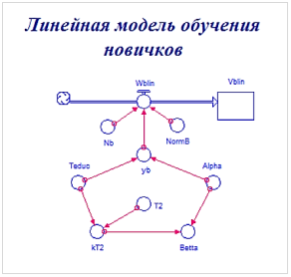
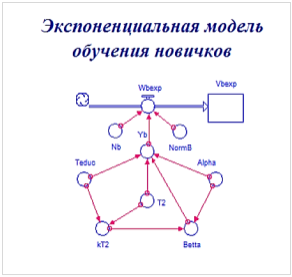
Рис. 3. Графические диаграммы причинных связей для линейной и экспоненциальной моделей обучения
Формулы для проведения моделирования указаны в таблице 2.
Таблица 2
Формулы для проведения имитационного моделирования
|
Формула для линейной модели |
Формула для экспоненциальной модели |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примечание *: вычисляется по формуле в iThink | |
В данной статье описаны линейная и экспоненциальная модели обучения отстающих учеников («новичков») и особенности их применения. Разработанные модели могут использоваться для исследования влияния моделей обучения на время выполнения необходимой нормы знаний.
Разумеется, разработанные модели применимы для «грубой» оценки, многие факторы в них не учитываются. Например, тот факт, что некоторые ученики в принципе не предрасположены к выходу на более качественный уровень знаний по математике. Кроме того, при обучении математике изучение некоторых новых тем не имеет смысла, пока ученики не запомнили информацию, принципы или основные формулы, которые необходимы для решения задач по ранее изложенному материалу. Однако для ситуации в целом данные модели могут оказаться весьма полезными. Разработка подобных имитационных моделей крайне важна, поскольку позволяет определить вектор дальнейших действий.
Литература:
- Кобелев, Н. Б. Имитационное моделирование: Учебное пособие / Н. Б. Кобелев, В. В. Девятков, В. А. Половников. — М.: Инфра-М, 2016. — 448 c.
- Девятков, В. В. Имитационное моделирование: Учебное пособие / Н. Б. Кобелев, В. А. Половников, В. В. Девятков. — М.: КУРС, НИЦ Инфра-М, 2013. — 368 c.
- А. А. Воронов. Введение в динамику сложных управляемых систем. ‒ М.: Наука, 1985. — 352 с.