В статье автор пытается оценить валютный рынок Великобритании с помощью множественной линейной регрессии. Основная гипотеза работы заключается в том, что полученное распределение будет схоже с нормальным распределением.
Ключевые слова: регрессия, валюта, валютный рынок, аппроксимация, Великобритания.
Валютный рынок Великобритании является одним из самых результативно организованных и занимает значимое место на международной экономической арене.
Удивительным фактом является то, что население Великобритании от мирового занимает только 1 %, но доля ВВП Великобритании в международном пространстве составляет 3 %. Таким образом, валютный рынок Великобритании занимает 5 место в мире по рациональности осуществления валютных сделок.
Также валютный рынок Великобритании является одним из самых стабильных, что достигается устойчивой экономической системой и политическим положением, которое имеет все характеристики авторитетности в мире.
Валютный рынок Великобритании обладает высокими показателями выгодности заключения валютных операций, что позволяет Великобритании обладать самым низким уровне безработицы и инфляции в мире.
Но это не значит, что валютный рынок Великобритании не переживал кризисные времена, совсем наоборот, валютный рынок Великобритании не раз оказывался на грани полного краха, но благодаря своевременным и экономически точным действиям государства, он вновь занимал лидирующие позиции, причем за максимально короткое время.
Одной из важных составляющих валютного рынка Великобритании являются активы самых богатых людей мира, которые доверяют осуществлять операции по купле-продаже валюты банкам Великобритании, что приносит им прибыль несоизмеримых размеров. Кроме того, валютный рынок Великобритании оказывает влияние на все остальные валютные рынки мира и на принцип осуществления всех сделок по купле-продаже валюты. Решение Великобритании в экономической области всегда является приоритетным в независимости связано ли оно с валютной сферой, либо с другими сферами международных отношений.
Валютный рынок Великобритании в настоящее время является примером организации сделок по купле-продаже валюты для всего мира.
Для решения задачи оценки выявления значимых предикторов воспользуемся финансовым порталом Финам.ru [1]
Список предполагаемых предикторов может быть выбран следующем образом:
– Индекс S&500
– Золото
– Биткоин
– Нефть.Брент
– Швейцария франк / USD
– Euro / USD
– Платина
– Норвегия крона / USD
Для проверки статистических гипотез был использован язык программирования R.
Для дальнейшего анализа необходимо перейти к логарифмическим доходностям.
Использование множественной линейной регрессии. Предположим, что t представимо в виде μt=β0+β1xt,1+...+βpxt,p.
Где xt,k, k=1,...,p — известные постоянные. Обычно в качестве таких переменных берут величины, которые находятся под контролем экспериментатора и измеряются с пренебрежимо малой ошибкой, а β0,β1,...,βp — неизвестные параметры, подлежащие оценке.
Пусть значения xt,k изменяются и исследователю доступны n их различных наборов и при этом наблюдается nn значений Y1₁,Y2,...,Yn переменной Y, тогда:
Yt=β0+β1xt,1+...βpxt,p+ϵt, t=1,...,n
Или в матричной форме
Y=Xβ+ϵY
Здесь мы предположили, что xt,0=1,i=1,...n
Maтрица X размера (n×p+1) называется регрессионной матрицей. Переменные xt,k,k=1,...,p обычно называют независимыми переменными, регрессорами или предикторами, а переменную Yt называют зависимой переменной или откликом.
Пример 1. Пусть xt,k=t k . Получаем полиномиальную модель
Yt=β0+β1t+...βptp+ϵt, t=1,...n.
Пример 2. Пусть t — интерпретируется как время и принимает значения 1,2,...n. xt,k=xt−k лаговая переменная, т. е. переменная с временной задержкой в к единиц времени, тогда:
Yt=β0+β1xt−1+...βpxt−p+ϵt, t=1,…n
Последнюю модель называют моделью авторегрессии порядка p. Общим в этих примерах является то, что они линейны по отношению к неизвестным параметрам β0,β1,...,βp. Поэтому модель называют линейной регрессионной моделью.
Оцениваем исходную модель константой:
Y t = β0+β1xt,1+...βpxt,p+ϵt
Определение значимых и незначимых предикторов. Гораздо удобнее определить через таблицу корреляции. Незначимыми предикторами будем называть те, что близко к нулю (низкокоррелируемые), а значимыми те, что ближе к 1 (коррелируемые) или — 1 (обратно коррелируемые). Отметим, что разницы между построением таблицы по начальным данным или по логарифмической доходности нет.
Проиллюстрируем на рис. 1.
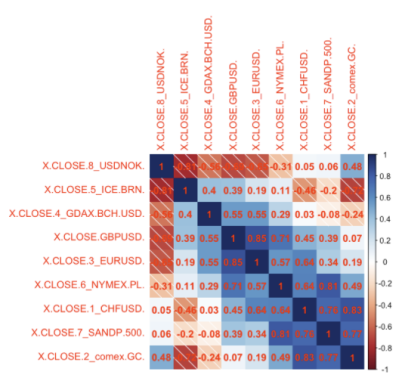
Рис. 1. Таблица корреляции
Анализ остатков. После оценки регрессионной модели можно получить оценку процесса x t , а именно x t =y t −μ t , которые будем назвать остатками. Если модель тренда была выбрана корректно, то поведение процесса остатков должно быть адекватно предположениям относительно процесса x t перед оценкой модели.
Например. Если предполагалось, что процесс x t белый шум, то процесс остатков x t тоже должен быть белым шумом. Если это не выполняется, это означает, что выбранная модель тренда не учитывает всей специфики динамики ряда.
О распределении остатков можно сделать предположения, если посмотреть на гистограмму остатков.
Проиллюстрируем на рис. 2.
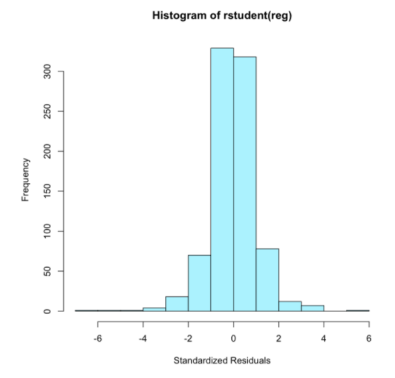
Рис. 2. Гистограмма регрессионной модели
Вид гистограммы наводит на мысль о нормальном распределении остатков. Нормальность остатков может быть проверена различными способами. Начнем с графического, так называемого нормального квантиль-квантиль (QQ) графика. Для нормально распределенных случайных величин QQ график должен выглядеть как прямая. Для остатков сезонной модели QQ график будет таким:
Проиллюстрируем на рис. 3.
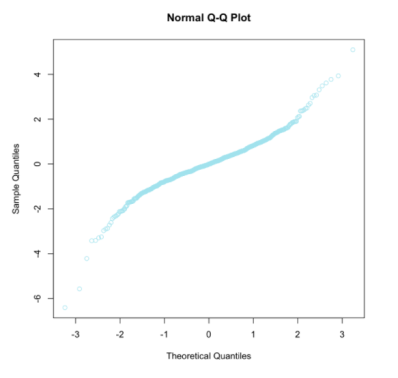
Рис. 3. Квантиль-квантиль график для регрессионной модели
Вот так он выглядит для нормального распределения. Загнутость на концах графика говорит о распределениях с тяжелыми хвостами.
В итоге имеем регрессионную модель, которая имеет достаточно хорошую обоснованность и правдоподобие. Главным выводом является гипотеза о том, что валютный рынок Великобритании может быть аппроксимирован нормальным распределением.
Литература:
1. Финансовый портал Финам.ру. URL: https://www.finam.ru/ (дата обращения 06.12.2021)

