В статье рассматривается теорема Пикара и доказывается существование решения задачи Коши методом последовательных приближений.

Ключевые слова: метод последовательных приближений, теорема Пикара, существование решения задачи Коши, условие Липшица.

Постановка задачи Коши. Теорема Пикара.

Рассмотрим задачу Коши

(1.1)

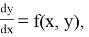
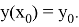
Функция задана в области G плоскости , содержащий замкнутый прямоугольник Предположим, что выполнены следующие условия:

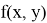
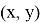
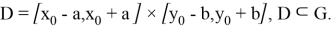
1) Пусть непрерывна в области по совокупности переменных и, следовательно, (по теореме Вейерштрасса) равномерно ограничена там. Тогда существует постоянная

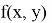
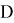
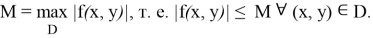
2) Пусть удовлетворяет в условию Липшица по переменной , т. е. постоянная Липшица , не зависящая от и .

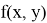
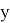
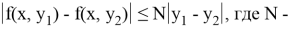
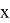
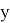
Теорема (существования и единственности решения задачи Коши).

Пусть выполнены условия 1) и 2). Тогда на отрезке

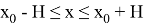
существует единственное решение задачи (1.1).

Следующее утверждение существенно используется при доказательстве сформулированной теоремы.

Лемма 1. Пусть функция непрерывна по совокупности переменных в некотором прямоугольнике Тогда задача Коши (1.1) эквивалентна интегральному уравнению

(1.2)

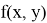
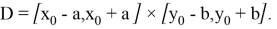
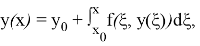
которое рассматривается в классе непрерывных функций.

Доказательство: Пусть решение (1.1), целиком лежащее в D. Тогда, подставляя его в (1.1) и интегрируя полученное тождество в пределах от до получим, что удовлетворяет уравнению (1.2).

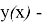
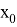
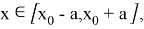
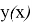
С другой стороны, если непрерывная функция является решением (1.2), то также непрерывна, а

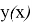
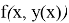
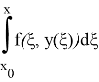
является непрерывно дифференцируемой функцией переменной . Следовательно, решение дифференциального уравнения

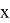
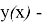
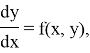
удовлетворяющее начальным условиям y(

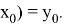
Итак, мы показали эквивалентность задачи (1.1) и (1.2).

Доказательство существования решения задачи Коши.

Для доказательства теоремы применим метод последовательных приближений (метод Пикара). Определим итерационный процесс метода последовательных приближений так:

(1.3)

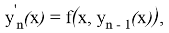
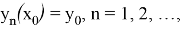
где произвольная непрерывная функция, график которой целиком лежит в области D. На каждой итерации задача (1.3) разрешима, и ее решение при представимо в виде

(1.4)

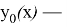
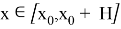
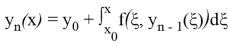
Далее, в силу условия имеем Поэтому интегральная кривая не покинет угол между диагоналями прямоугольника и, следовательно, В результате получим некоторую функциональную последовательность Исследуем ее свойства.

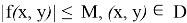
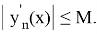
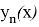
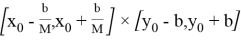
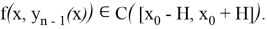
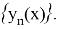
Лемма 2. Функциональная последовательность сходится равномерно на множестве .

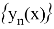
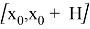
Доказательство: Рассмотрим функциональный ряд

(1.5)

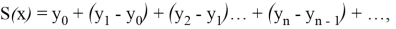
Оценим абсолютные величины членов ряда (1.5):

(1.5')

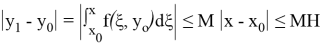
далее,

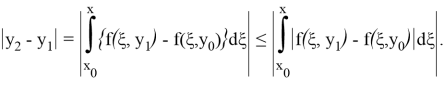
На основании условия Липшица подынтегральная функция удовлетворяет неравенству

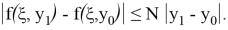
Теперь

(1.5'')

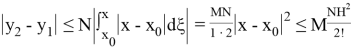
Аналогично получим:

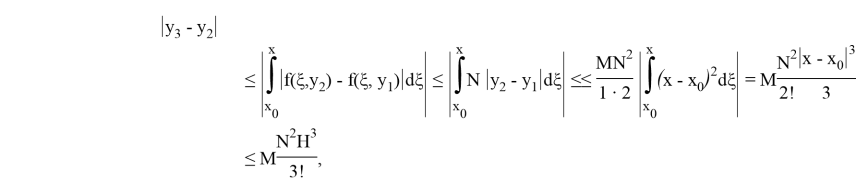
и наконец

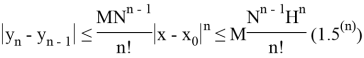
Далее

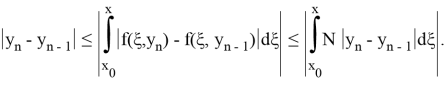
Подставив в последний интеграл вместо выражение получаем:

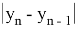
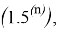
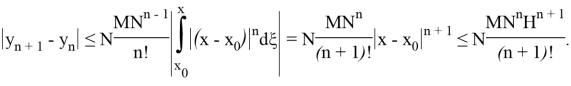
Теперь, учитывая замену его наибольшим допустимым значением H, мы приходим к заключению, что каждый член ряда (1.5) меньше соответствующего члена числового ряда с положительными членами:

(1.6)

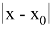
По признаку Даламбера мы получаем

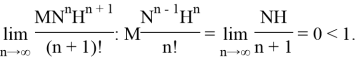
Следовательно, ряд сходится абсолютно и равномерно на множестве (признак Вейерштрасса), а значит функциональная последовательность также сходится равномерно на множестве т. е.

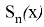
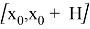
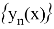
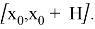
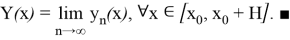
Докажем, что полученная таким образом функция удовлетворяет интегральному уравнению (1.2).

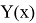
Возьмем равенство (1.4):

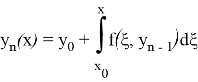
и перейдем к пределу при

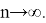
Благодаря равномерной непрерывности функции по мы для любого наперед заданного положительного числа ℇ можем найти такое что неравенство

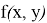
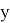
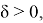
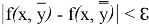
будет выполнено для тех пар точек и области D, для которых выполняется неравенство (в силу условия Липшица достаточно взять ). Далее, из равномерности стремления последовательности к пределу вытекает возможность для выбранного так подобрать натуральное число , чтобы при для всех значений в интервале имело место неравенство:

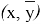
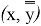
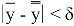
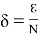
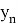
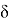
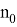
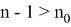
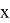
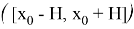
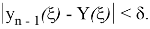
Сопоставляя оба эти неравенства, мы получаем при

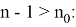
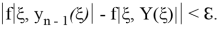
Отсюда следует:

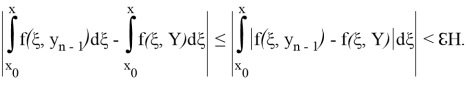
Пользуясь произволом числа ℇ, находим:

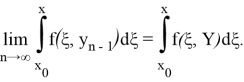
Таким образом, переходя к пределу в (1.4) при , получаем тождество:

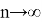
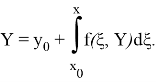
т. е. удовлетворяет интегральному уравнению (1.2).

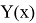
Лемма 3. Функциональная последовательность сходится к непрерывному решению интегрального уравнения (1.2), записанного выше.

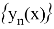
Доказательство: Поскольку все функции непрерывны, а функциональная последовательность

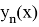
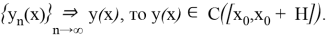
Кроме того, равномерная сходимость непрерывных функций является достаточным условием для перехода к пределу под знаком интеграла в выражении (1.4). В результате получим

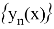
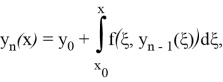
т. е. предел последовательных приближений удовлетворяет интегральному уравнению (1.2), эквивалентному задаче Коши (1.1). Итак, существование решения задачи Коши для скалярного уравнения доказано.■

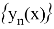
Литература:

1. Исраилов С. В., Юшаев С. С. Многоточечные и функциональные краевые задачи для обыкновенных дифференциальных уравнений. Нальчик, «Эль-Фа» 2014 г.
2. Исраилов С. В. Исследование некоторых многоточечных краевых задач для обыкновенных дифференциальных уравнений с непрерывными правыми частями и с сингулярностью: Дис. канд. физ.-мат. наук. Баку. 1964 г.