Электронные устройства сверхвысокочастотного диапазона широко применяются во многих сферах деятельности человека как в гражданской, так и в военной промышленности. Важным компонентом таких электронных устройств является замедляющая. Для разработки более совершенных приборов в терагерцовом диапазоне необходимо исследование и расчет характеристик замедляющей системы. Объектом исследования является система типа «петляющий волновод». Для расчета характеристик была построена трехмерная модель, заданы условия симуляции и получены Z-параметры. Обработав результаты были получены основные электродинамические характеристики «петляющего волновода».
Ключевые слова : замедляющая система, петляющий волновод, дисперсионные характеристики.
Замедляющие системы предназначены для уменьшения фазовой скорости электромагнитных волны, которые проходят вдоль оси системы, по сравнению со скоростью в свободном пространстве [1]. Данные системы используются в усилительных и генераторных вакуумных приборах для настройки фазовой скорости электромагнитных волн и получения режима синхронизации, который необходим для генерации и усиления. Развитие технологий в микроволновом диапазоне и расширение области их применения привело к возникновению новых проблем, которые связаны с проектированием и использованием новых устройств. На данный момент выходная мощность и полоса частот устройств определяется видом используемой замедляющей системы. Поиск, исследование и проектирование новых замедляющих систем для вакуумных приборов является актуальной проблемой в микроволновом диапазоне частот, поскольку на сегодняшний день терагерцовый диапазон представляет собой наименее освоенный участок электромагнитного спектра. Выбор замедляющей системы типа «петляющий волновод» в устройствах миллиметрового диапазона обуславливается простотой конструкции и относительной простотой расчета дисперсионных характеристик.
Свойства замедляющих систем в качестве линий передачи электромагнитной волны характеризуются несколькими параметрами, которые описывают функции, которые выполняет замедляющая система в электронных приборах. Основными характеристиками замедляющих систем являются коэффициент замедления, дисперсионная характеристика, частотный диапазон, сопротивление связи, затухание волны и предельная передаваемая мощность. [2].
Исследование электродинамических характеристик замедляющей системы состоит из двух основных этапов: построение трехмерной модели волновода среде моделирования СВЧ структур и анализ полученных параметров через среду для технических вычислений. Моделирование производилось в программе Ansys HFSS, поскольку данная программа является наиболее популярной средой для электродинамического моделирования и проектирования [3]. Для построения трехмерных моделей электромагнитных полей программа использует метод конечных элементов, суть которого заключается в разбиении области поиска решения на конечное количество элементов. Для получения характеристик выбран тип решателя «Driven Modal», граничные условия «Perfect E», что означает идеальный проводник, а также заданы волновые порты «Wave Port». Значение рабочей частоты для исследуемого волновода равно 70 ГГц. Количество итераций — 12. Количество итераций влияет на процесс адаптивного генерирования сетки модели. Частотный диапазон для расчетов имеет значения от 60 ГГц до 80 ГГц.
Для исследования электродинамических характеристик волновода необходимо получить матрицы Z-параметров. Z -параметры описывают поведение электрических линий передачи. Данный тип параметров также называют параметрами импеданса. Расчет матриц параметров осуществляется в программе Ansys HFSS. Для получения матриц необходимо построить зависимость выбранных параметров по заданной частоте.
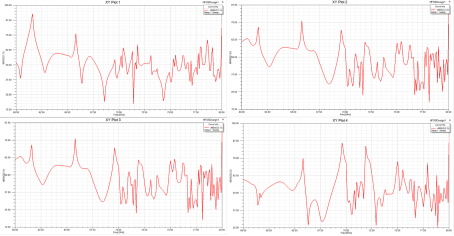
Рис. 1 Зависимость элементов матрицы Z-параметров в частотном диапазоне 60–80 ГГц
Полученные Z-параметры были преобразованы A-матрицу перехода. Переход осуществляется через формулу преобразования [4].
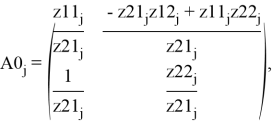
Результатом преобразования является массив матриц размерностью 2x2 для каждого значения частоты. Для дальнейшего построения электродинамических характеристик необходимо рассчитать собственные числа и вектора для каждой матрицы в диапазоне частот. Поскольку частотный интервал составляет 20 ГГц с шагом в 0.1 ГГц, то необходимо найти значения для 201 матрицы размерностью 2x2. Расчет данных параметров производился на языке Python с использованием сторонней библиотеки Numpy. Нахождение собственных чисел и собственных векторов производится через математическую функцию «.eig» [5].
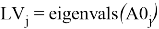
Результатами выполнения функции «.eig» является набор из шести комплексных чисел для каждого значения частоты. Собственное число является комплексным (exp(±α±jφ), в котором действительная часть определяет реактивное затухание, а мнимая часть — набег фазы на ячейку. Логарифм двух собственных чисел отличается только знаком, поэтому значения можно взять по модулю.
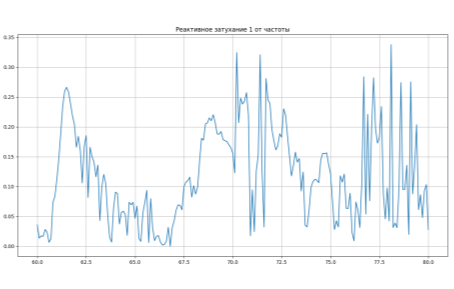
Рис. 2 Зависимость реактивного затухания в выбранном частотном диапазоне
Помимо нахождения собственных чисел были найдены собственные вектора A-матрицы.
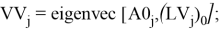
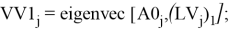
Собственные вектора также являются комплексными числами. Каждому собственному числу соответствует два значения собственных векторов. Одно значение собственного вектора определяет напряжение, другое значение определяет ток в сечении порта. Для поиска характеристического напряжения необходимо найти отношение напряжения и тока для каждого из собственных чисел.
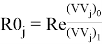
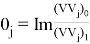
В результате расчетов в программе на языке Python был получен массив комплексных чисел. Каждому значению частоты соответствует два комплексных числа.
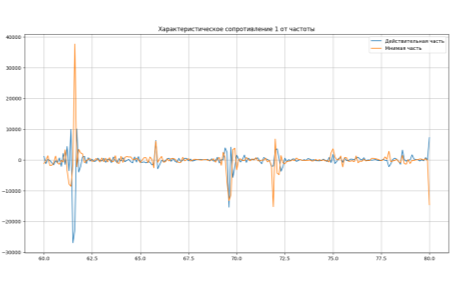
Рис. 3. Зависимость действительной и мнимой части характеристического сопротивления в частотном диапазоне 60–80 ГГц для первого собственного числа
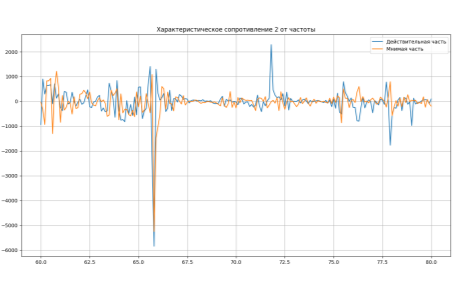
Рис. 4 Зависимость действительной и мнимой части характеристического сопротивления в частотном диапазоне 60–80 ГГц для второго собственного числа
График отношения коэффициента замедления в выбранном частотном диапазоне является дисперсионной характеристикой волновода. Для поиска коэффициента замедления необходимо найти логарифм двух собственных векторов.
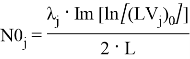
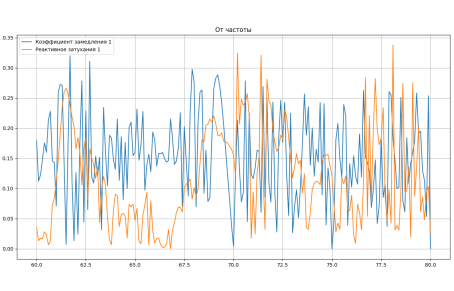
Рис. 5. Зависимость коэффициента замедления и реактивного затухания в частотном диапазоне 60–80 ГГц
Анализируя полученный график, зависимости коэффициента замедления от реактивного затухания, можно увидеть, что дисперсия существует практически по всей структуре волновода. Повышение частотной избирательности рассматриваемой конструкции может понизить хаотичность поведения дисперсионных характеристик. Изменение геометрических размеров отдельных частей волновода может привести к изменению дисперсионных характеристик.
Литература:
- Силин Р., Сазонов В. Замедляющие системы / под ред. Шалимова Г. Москва: Советское радио, 1966. 628 с.
- Силин Р., Алмазов-Долженко К. Замедляющие линии передачи СВЧ // СВЧ-Электроника. 2019. Т. 4. С. 9.
- Банков С., Курушин А., Разевиг В. Анализ и оптимизация СВЧ структур с помощью HFSS. 2004. С. 283.
- Кравченко Н., Мухин С., Пресянков С. Замедляющие системы миллиметрового диапазона // T-comm. 2015. Т. 6. С. 63.
- Мухин С. Анализ дисперсионных характеристик замедляющих систем типа цепочек связанных резонаторов вблизи границ полосы пропускания // Радиотехника и электроника. 2012. Т. 11. С. 11.

