В статье автор строит модель блокчейн сети, основанной на «доказательстве работы» (PoW). Проведен математический анализ модели. Выполнено численное моделирование работы сети при различном количестве участников. Применена линейная регрессия для собранных данных в ходе моделирования работы сети. Была получена модель, позволяющая находить интересующие параметры (сложность, время) по начальным данным.
Ключевые слова : blockchain, machine learning, proof-of-work.
Анализ математической модели blockchain
В данной статье, количество ведущих нулей в результате работы hash-функции используется в качестве параметра сложности для упрощенных выражений.
Введем некоторые определения:
– D > 0 — сложность сети, определяет количество ведущих нулей hash блока
– n > 0 — количество вызовов hash-функции
Блок в blockchain содержит поле hash, для проверки корректности найденного при помощи hash-
функции hash, процессор отделяет D ведущих 16-ричных значений битов и проверяет их на равенство 0. Процесс продолжается до тех пор, пока не будет найдено значение hash-функции, в котором количество 0 больше или равняется D.
Используя данные предположения, мы можем построить корреляцию между количеством hash n, трудностью D и показать как эти параметры влияют на вероятность успеха. Ниже рассматриваются два случая при n =10 и n = 15, это позволяет наблюдать как изменяется вероятность успеха, но при этом мы видим, что в обоих случаях после достижения сложности определенного уровня (в данном случае 10−11 и 15−16) вероятность успешного mining у одного человека стремится к 0.
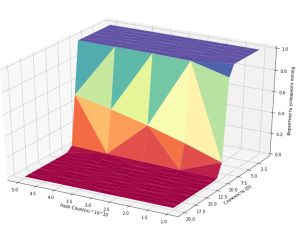
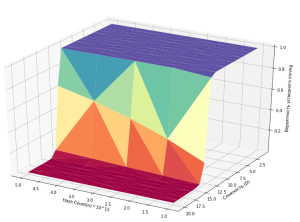
Математическая модель
Дальнейшим шагом является построение математической модели. Формула будет сформулирована как продолжение математической модели, основанной на неоднородном Пуассоновском процессе. И применить полученный результат без изменения к реальным блокчейн системам нельзя.
Полученную формулу в рамках данного этапа можно записать в виде:
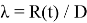
Достоинства и недостатки математической модели
Перед тем как использовать полученную формулу, нужно осознавать ее ограничения:
– невозможно использовать без изменений для полноценных блокчейн систем
– решает очень узкую задачу, которая в реальном мире мало где встречается
– для ее проверки и симуляции потребовалось реализовать отдельный скрипт, который не имеет ничего общего с blockchain сетями
Также стоит упомянуть достоинства:
– формула получилась очень простой и ее легко использовать без сложных вычислительных ресурсов
– моделировать процесс для данной математической модели достаточно просто
Сравним, как показывает себя формула при различных параметрах D и R. Нас интересует погрешность, а именно loss:
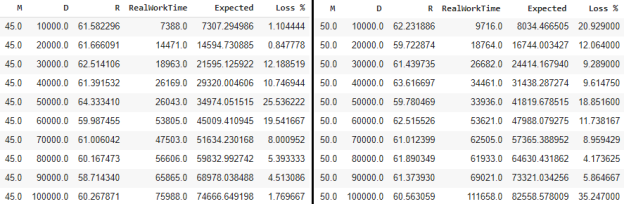
Применяя данную формулу на мы получим следующие результаты, которые как мы видим с незначительными погрешностями, несмотря на некоторые «выбросы»в результатах. Выбросы у нас появляются из-за недостаточно большой выборки, как можно заметить тут мы взяли M= 45,50. При больших значениях мы увидим, что loss уменьшается до 1−2 %:
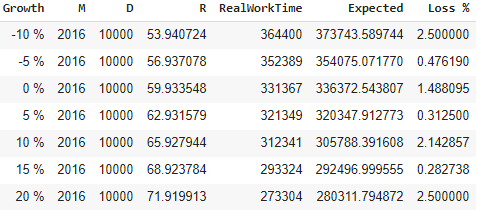
Прогнозирование с помощью Machine Learning
Далее был реализован алгоритм с применением линейной регрессии, который позволил по начальным данным найти значение FullTime т.е сколько займет времени целиком процесс по добыче нужного колличества блоков:
– T — желаемое время между блоками задачи и формировать формулы под определенный случай
– V — число валидаторов в блокчейн сети
– D0 — начальная сложность сети
– DAvarage — этот параметр не является начальным, мы его будем вычислять, используя ранее обученную модель для нахождения DAvarage
– R — скорость сети(hash Rate), количество вызовов hash-функции в единицу времени, от одного участника сети т. е. V.
Алгоритм линейной регрессии был выбран за простоту, можно использовать где требуется и легко интерпретировать модель и надежность. Линейная регрессия почти никогда не переобучается и это достаточно простой алгоритм для реализации. При попытках применить более сложные модели они недавали никакого прироста в эффективности, поэтому было принято решение остановиться на линейной регрессии. Первым шагом будет применение ранее обученной модели для вычисления DAvarage, после вычисления мы добавляем как дополнительный столбец и в итоге мы имеем следующий dataFrame:
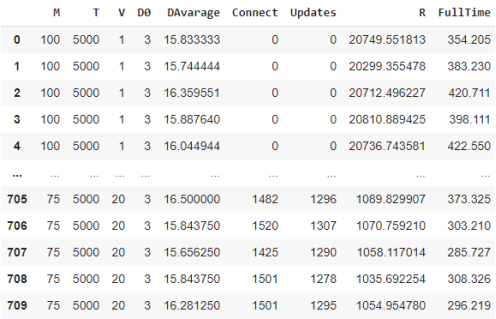
Далее, для более полного понимания содержимого dataFrame посмотрим на распределение величин в нем:
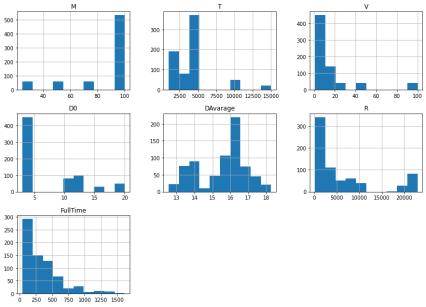
После этого применяем StandardScale для масштабирования данных и обучаем модель предварительно разделяя на обучающую и тестовую выборку и получаем в результате:

Как мы видим, получается достаточно хорошая погрешность, это позволяет нам считать, что такой подход можно применять для прогнозирования времени, которое будет потрачено на процесс.
В данной статье были рассмотрены некоторые из возможных способов для моделирования процесса добычи блоков в зависимости от выбранных параметров. В рамках моделирования ожидаемого времени для добычи N блоков при построенной модели на теории пуассоновских процессов была достигнута точность дающая loss 5−10 %. Для того чтобы улучшить данный показатель был изучен механизм интервала ретаргентинга и показано что при увеличении параметра N та же самая модель дает уже 0.3−2 %. Из-за ограниченности данной модели далее была реализована своя собственная блокчейн-сеть и на данных, выдаваемых ею, были применены средства машинного обучения. Реализованная модель на основе линейной регрессии показала в результирующих метриках очень хорошие результаты, что дает повод для дальнейшего изучения данных подходов.
Литература:
- Papadis, N, Stochastic Models and Wide-Area Network Measurements for Blockchain Design and Analysis, 2018.
- Satoshi Nakamoto, Bitcoin: A Peer-to-Peer Electronic Cash System, 2009.
- David Cox, Roger Wattenhofer, Some Statistical Methods Connected With Series of Events, 1955







