В статье автор исследует поведение клеточного автомата «муравей Лэнгтона» на геометрической фигуре тор, который представлен в развертке и представляет собой клетчатый лист.
Ключевые слова: клеточный автомат, муравей Лэнгтона, торическая решетка
Совсем недавно интерес математиков и специалистов в компьютерных науках вызвал клеточный автомат, созданный Крисом Лэнгтоном [4], который чаще всего теперь называют «муравей Лэнгтона» [3; 2].
Оригинальные правила эволюции этого автомата подразумевают наличие бесконечного во все стороны клетчатого поля. Наша работа посвящена изучению версии автомата, в которой в качестве поля выступает торическая решётка фиксированного размера. Более подробно, перед нами стояли следующие цели и задачи:
- Изучить правила эволюции муравья Лэнгтона, подробно изучить первые несколько ходов движения муравья.
- Дать определение плоского тора, изучить поведение муравья на нескольких видах торов небольшого размера.
- Проанализировать эволюцию некоторых торов размера n для произвольного натурального n.
- Сформулировать и доказать теорему об эволюции клеточного автомата «муравей Лэнгтона» для произвольного n.
При решении поставленных задач мы пользовались более или менее стандартными методами комбинаторики [1].
Муравей Лэнгтона — это так называемая двумерная машина Тьюринга с очень простыми правилами. Здесь «муравей» движется по бесконечной плоскости, разбитой на клетки, покрашенные, некоторым образом, в чёрный и белый цвет. Пусть в одной из клеток находится «муравей», который на каждом шаге может двигаться в одном из четырёх направлений в клетку, соседнюю по стороне. Муравей движется согласно следующим правилам:
- На чёрном квадрате — повернуть на 90° влево, изменить цвет квадрата на белый, сделать шаг вперед на следующую клетку.
- На белом квадрате — повернуть на 90° вправо, изменить цвет квадрата на чёрный, сделать шаг вперед на следующую клетку.
В нашем случае муравей будет перемещаться по плоскому тору (торической решётке).
Понятно, что основное отличие от случая эволюции на плоскости заключается в том, что теперь поле состоит из конечного числа клеток. Поскольку количество всевозможных раскрасок этих клеток в два цвета и количество возможных положений муравья конечно, рано или поздно возникнет конфигурация, которая уже была. Более того, понятно, что по данной конфигурации мы можем восстановить предыдущую однозначно, откуда следует, что первая повторившаяся конфигурация — это и есть самая первая конфигурация.
Мы будем рассматривать случай, когда изначально все клетки торической решётки белые.
Для вычисления количества ходов, через которые муравей «возвращается» в исходное, а поле «становится» белым, мы написали программу в среде Pascal. Также программа считает, сколько раз поле становилось белым.
Таблица 1
Результаты расчётов
|
Сторона тора (n) |
Кол-во раз, когда поле становилось белым |
Кол-во ходов, через которые поле первый раз становилось белым |
Кол-во ходов до возвращения муравья в исходное положение |
|
2 |
1 |
8 |
8 |
|
3 |
3 |
22 |
66 |
|
4 |
1 |
96 |
96 |
|
5 |
5 |
2342 |
11710 |
|
6 |
1 |
4592 |
4592 |
|
7 |
7 |
9166514 |
64165598 |
|
8 |
1 |
11502464 |
11502464 |
Из этих данных видно, что у торов с нечётным n число m равно числу n, а у торов с чётным n число m равно единице. Возникает гипотеза, что так дело будет обстоять всегда, для произвольных n.
Из этой гипотезы возникает теорема: если n=p, где р — простое нечётное число, причём первый раз, когда поле становилось, муравей не был в исходной клетке, но смотрел в ту же сторону, что и вначале, то m=n.
Рассмотрим доказательство данной теоремы. На рисунке 1 муравей находится к клетке (0;0).
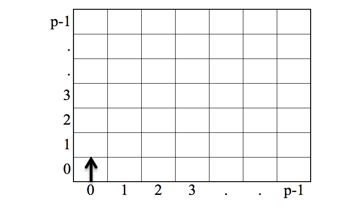
Рис. 1. Произвольная торическая решётка
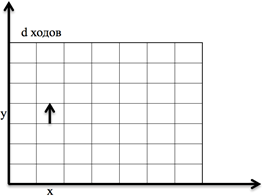
Рис. 2. Произвольная торическая решётка в координатной плоскости
На рисунке 2 муравей переместился от исходного положения на d ходов, и мы поместили решётку в координатную плоскость. Координаты муравья будут (x;у). Тогда через 2d ходов его координаты будут (2x;2у), а через kd ходов (kx;ky).
Предположим, что kx нацело делится на р, ky нацело делится на р, причём x < p и не равно 0, либо у < p и не равно 0, тогда х и р взаимно простые числа, y и р взаимно простые числа. Следовательно, наименьшее k, при котором kx нацело делится на р, это и есть. Теорема доказана.
Итак, мы решили все поставленные во введении задачи; проанализировали поведение муравья Лэнгтона на простейших торических решётках, сформулировали гипотезу и доказали теорему для произвольного n.
Литература:
- Виленкин Н. Я. Виленкин А. Н., Виленкин П. А. Комбинаторика. — М.: МЦНМО, 2007.
- Boon J. P. How fast does Langton’a ant move? Preprint, see arXiv: cond-mat/0004331, 8 p.
- Gajardo A., A. Moreira, E. Goles. Complexity of Langton’s ant. Discrete Applied Mathematics 117 (2002), № 1–3, 41–50.
- Langton C. G. Studying artificial life with cellular automata, Physica D: Nonlinear Phenomena 22 (1986), № 1–3, 120–149.

