Абстрагирование позволяет изучать различные разделы физики и получать информацию для решения конкретных технических задач. В статье рассмотрены некоторые элементы метода абстрагирования на примере различных физических идеализаций.
Ключевые слова: абстрагирование, идеализация, физическая модель, физический эксперимент.
Разработка принципиально новых видов вооружений и техники, их защита базируются на стабильных повторяющихся физических законах природы. Процедура познания этих закономерностей многогранна. Она включает множество процессов, эмпирических и теоретических приемов, методов (наблюдение, осмысление, абстрагирование и прочее), осуществляемых на практике в учебном процессе военного вуза.
Среди универсальных методов познания выделяется абстрагирование, так как его результатом является построение физической модели без мысленного акцента на некоторых сторонах изучаемого явления или процесса.
Абстрагирование — это метод научного познания, состоящий из реализации трех последовательных операций: 1) сознательном отвлечении от некоторых свойств познаваемого объекта (как несущественных в данном контексте или уже известных науке); 2) фиксации других свойств этого объекта как важных или новых; 3) приписывание этим свойствам статуса объекта (например, свет, длина, масса) [1, c.59].
Процесс абстрагирования сложен и многоступенчат.
Во-первых, проводится разделение значимого и несущественного, вычленение главного для конкретного исследования, оценка разных факторов.
Во-вторых, устанавливается независимость или пренебрежимо малая зависимость изучаемых физических явлений, процессов от внешних условий, конкретных факторов.
В-третьих, осуществляется замещение конкретного объекта (или явления) другим, представляющим собой физическую модель. Так в классической динамике при решении задач на перемещение массивного тела его заменяют материальной точкой с определенной массой, но размерами тела в условиях данной задачи пренебрегают. В электростатике вместо объемного электрического заряда вводят точечный электрический заряд, приписывая его материальной точке.
Способы и приемы абстрагирования разнообразны в зависимости от физического объекта и цели абстрагирования.
Основные функции абстрагирования позволяют заменить в познании сложное простым, сохраняя главное в описании физического объекта, выделяя его различные стороны и свойства, их относительную независимость, устанавливая связи между ними.
Одним из видов абстрагирования является идеализация, то есть мыслительный акт, связанный с образованием абстрактных объектов, не имеющих своего аналога в действительности [2, c. 186], например:
1) абсолютно упругий удар, представляющий модель кратковременного соударения тел, в которой пренебрегают деформациями физических объектов, и полная механическая энергия сохраняется;
2) идеальный газ, имеющий частицы пренебрежимо малых размеров, которые не обладают дальнодействующим взаимодействием друг с другом;
3) нерастяжимая и невесомая нить, то есть физический объект, массой и изменением размеров которого пренебрегают в условиях данной задачи.
Идеализация может реализовываться всевозможными способами и приемами, базируясь на разных видах абстракции. Абстрагируясь от одних свойств реальных физических объектов, вводят модель, которой присущи только эти конкретные свойства. Например, изучая закон всемирного тяготения, мы рассматриваем тела как материальные точки. Геометрией и размерами физических объектов в данном случае пренебрегаем.
Прибегать к идеализации нас заставляют трудности представления реального физического объекта или процесса, так как от модели легче переходить к изучению реального процесса или явления. Например, трансформация уравнения состояния идеального газа Менделеева-Клайперона в качественное уравнение Ван-дер-Ваальса для реального газа осуществляется введением двух констант, учитывающих силы межмолекулярного притяжения и недоступность для движения молекул некоторого пространства. А знание законов колебаний математического маятника позволяет описывать реальные колебания любой сложности.
Заменяя изучение физического маятника его моделью, получаем возможность исследовать закономерности протекания колебательных процессов в зависимости от параметров самой колебательной системы (амплитуды А, циклической частоты
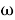
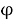
При решении задач на гармонические колебания используют дифференциальное уравнение
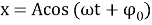
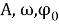
В силу ряда обстоятельств каждая конкретная идеализация обладает относительностью, так как не существует полностью независимого физического объекта от других форм материи. Такими причинами являются:
1) идеализация в процессе решения конкретного комплекса задач. Например, абсолютно черное тело, у которого поглощательная способность всего диапазона электромагнитного излучения максимальна (равна единице) при температурах выше абсолютного нуля. Значимость этой модели для решения вопроса о спектре теплового излучения любых физических тел дополняется проблемой равновесности данного вида испускания и коэффициента отражения. Они были разрешены только в рамках квантовой физики после введения модели «квант энергии»;
2) уточнение идеализации в ходе познавательного процесса, а иногда и ее замене. Например, модель строения атома Нагаока заменили планетарной моделью Резерфорда, а затем Резерфорда-Бора;
3) выявление ограниченности теорий, базирующихся на одной идеализации, в процессе применения;
4) абстрагирование и идеализация делают разнородные физические объекты однородными, что облегчает применение математических методов;
5) использование идеализации на эмпирическом и теоретическом уровнях научного познания. Результаты этих процедур относятся к идеальным системам, хотя они предназначены для применения к реальным объектам;
6) первоочередность эмпирического и теоретического уровней научного познания. В случае первоначальности физического эксперимента происходит создание теории с введенными физическими моделями, наделенными небольшим числом свойств и простой структурой. В качестве примера следует привести ядерную модель атома. Если теория со созданной физической идеализацией первична, то она объясняет проведенные или проводимые эксперименты. Например, появление идеализации «фотон» позволило объяснить явления фотоэффекта, давления света.
7) добавление допущений к измерительной системе и методике проведений физических измерений. Например, при введении понятия «температура» следует сообщить обучающимся о произвольных допущениях, связанных с выбором термометрической шкалы с целью представления температуры определенным числовым значением;
8) воспроизводимость физического эксперимента, связанного с созданием идеальной ситуацией и (или) идеализированного объекта, интересующих нас в данный момент времени. Следовательно, каждый физический эксперимент имеет дело с упрощенной репродуцируемой ситуацией.
В таблице 1 представлены некоторые способы, приемы абстрагирования и причины относительности выбранной физической идеализации.
Таблица 1
Некоторые элементы метода абстрагирования в физике
|
Способы, приемы |
Причины относительности физической идеализации |
|
Выделение главного. Абстрагирование от отдельных свойств. Введение физической модели с конкретными свойствами. |
Уточнение или замена. Решение комплекса физических задач. Ограниченность. Замена неоднородности физической системы однородностью. Применение к идеальным физическим объектам. Очередность теории и эксперимента в физике. Допущения к измерительной системе и методике проведения физических измерений. Воспроизводимость физического эксперимента. |
Использование на практических занятиях и лабораторных работах абстрагирования помогает обучающимся проводить операции над конкретно-чувственными представлениями как исходными данными созерцания и глубже воспринимать определенные проявления физических абстракций, способствуя повышению качества обучения физике.
Литература:
- Лебедев С. А., Лебедев К. С. Существует ли универсальный научный метод? — Тверь: Вестник ТвГУ, 2015. — Серия «Философия». — С. 56–72.
- Словарь иностранных слов / Ведущий редактор Л. Н. Комарова. — М.: Русский язык, 1988. — 624 с.

