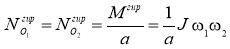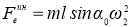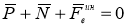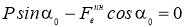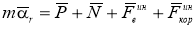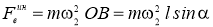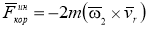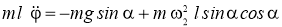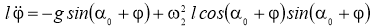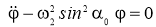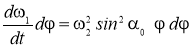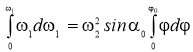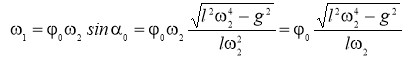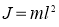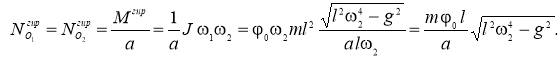Рассмотрена возможность определения гироскопических давлений на подшипники при использовании инерционных динамических гасителей колебаний маятникового типа.
Ключевые слова: инерционные динамические гасители колебаний маятникового типа, гироскопические давления на подшипники.
Рассматривается опыт использования инерционных динамических гасителей колебания при действии на объект, установленный на упругом фундаменте, двух возмущающих сил с различными частотами. Решение этой проблемы достигается путем использования двух инерционных динамических гасителей колебаний, если их настроить на резонанс с частотами возмущающих сил. При этом исследуются дифференциальные уравнения движения для системы с тремя степенями свободы.
Центробежный регулятор вращается вокруг вертикальной оси
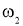
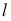
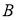
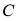
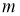
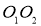
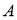
Расчётная схема центробежного регулятора представлена на рис. 1.
В результате возмущений регулятор может быть выведен из равновесного состояния и представлен самому себе. При отклонении стержня регулятора на малый угол
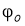
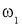
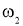
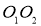
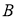
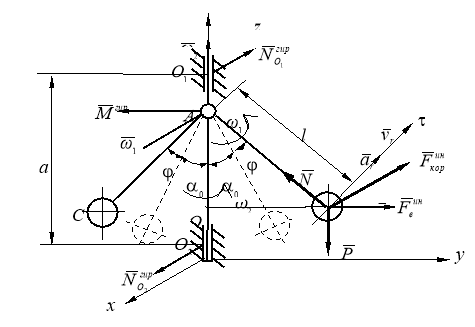
Рис. 1. Расчётная схема центробежного регулятора
Максимальные гироскопические давления на подшипники можно определить по формуле:
|
|
(1) |
где
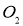
Так как маятник вращается с постоянной угловой скоростью
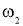
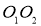
|
|
(2) |
Три силы
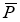
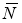
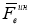
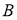
|
|
(3) |
Спроектировав уравнение (3) на касательную
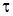
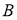
|
|
(4) |
По отношению к подвижной системе отсчёта
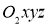
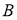
|
|
(5) |
где
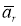
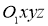
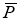
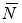
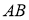
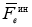
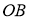
|
|
(6) |
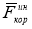
|
|
(7) |
где
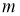
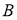
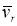
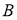
Эта сила
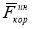
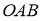
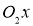
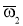
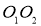
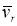
Спроектируем векторное уравнение (5) на касательную
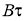
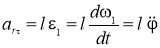
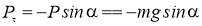
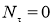
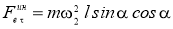
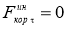
Получаем дифференциальное уравнение
|
|
(8) |
После преобразований уравнения (8), учитывая, что
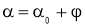
|
|
(9) |
Находим окончательно дифференциальное уравнение собственных малых колебаний маятника центробежного регулятора в относительном движении
|
|
(10) |
Для нахождения угловой скорости
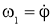
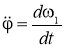
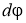
|
|
(11) |
Проинтегрируем
|
|
(12) |
Откуда находим
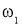
|
|
(13) |
Находим
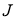
|
|
(14) |
Итак, после подстановки (13) и (14) в формулу (1) находим максимальные гироскопические давления на подшипники при применении гасителя колебаний маятникового типа при прохождении стержнем
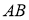
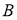
|
|
(15) |
Литература:
- Комкин А. И. Вибрация. Воздействие, нормирование. Защита //Безопасность Жизнедеятельности. М: Изд. Новые Технологии. 2004..№ 5, приложение стр.47.
- Серов М. В., Аверьянова Г. М., Александрова С. Г. Опыт применения теории колебаний к практическим вопросам применения инерционных динамических гасителей колебаний. Известия МГТУ «МАМИ» № 1(15), 2013, т. 3, с 118–124.