В статье рассматривается моделирование вынужденных крутильных колебаний системы с двумя степенями свободы.
Ключевые слова: вынужденные крутильные колебания, вал с жестко закрепленными дисками.
Среди упругих колебаний выделяются крутильные колебания тела, которые совершаются около оси, проходящей через центр инерции. Их анализ требует учета массы тела
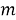
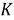
Крутильные колебания наблюдаются в технических устройствах разнообразного назначения (в том числе и военного), имеющих колебательные системы с двумя степенями свободы (например, вал с жестко закрепленными дисками). Потеря энергии в системе вследствие трения компенсируется при помощи периодического внешнего воздействия. В результате крутильные колебания становятся вынужденными незатухающими.
В нашей работе с помощью уравнений Лагранжа второго рода определяются собственные частоты вынужденных колебаний колебательной системы (вал — два жестко закрепленных диска), возникающих из-за внешней нагрузки, меняющейся по гармоническому закону.
Подобные механические системы широко используются в научных исследованиях и в технических устройствах. Они находят применение в датчиках для измерения параметров вязких сред [2, 3], гравиинерциальных приборах (например, гироскоп, гравиметрический датчик, гравиинерциальный навигационный комплекс) [4] и устройствах мехатроники различного предназначения (например, двигатель постоянного тока, дроны) [5, 6, 7].
Рассмотрим колебательную систему с двумя степенями свободы.
Исследуемая система состоит из: 1) невесомого вала; 2) двух массивных дисков. Оба конца вала радиусом r зафиксированы. На валу закреплены диски одинаковых масс m и радиусов R . Каждый и них расположен на расстоянии ℓ от соседнего ближнего конца вала. Расстояние между дисками также равно ℓ. Будем рассматривать случай, когда толщина дисков ∆ ℓ много меньше, чем длина отрезков вала, то есть ℓ >> ∆ ℓ.
Крутильная жесткость каждого участка вала одинакова и равна
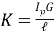
где G — модуль сдвига;
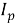
Полярный момент инерции относительно оси симметрии вала радиуса r определяется выражением
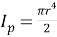
Представленная колебательная система имеет две степени свободы, связанные с углами кручения
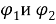
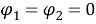
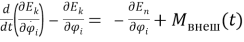
где
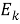
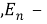
Запишем выражения для этих энергий через скорости изменения углов
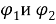
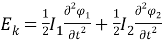
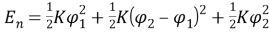
При этом внешний крутильный момент, приложенный к левому диску, изменяется со временем по гармоническому закону:
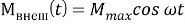
где
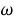
Моменты инерции дисков равны, так ка они имеют одинаковые массы и геометрические размеры
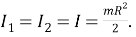
Подставив выражения (4) — (5) в уравнение Лагранжа (3), получим систему дифференциальных уравнений, описывающих вынужденные крутильные колебания:
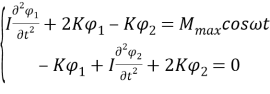
Найдем общее решение однородной системы дифференциальных уравнений, полагая, что углы кручения малы
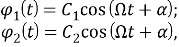
где
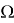
Подставляя выражения (8) в систему (7) с нулевыми правыми частями, получим систему алгебраических уравнений для амплитуд
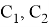
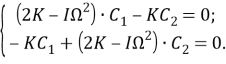
Для существования решения определитель системы (9) приравняв к нулю, получим
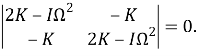
Из этого следует вековое уравнение для нахождения собственных частот
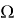
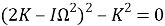
Следовательно, собственные частоты определяются выражениями:
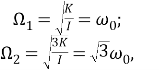
где
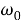
Собственная крутильная частота вала, закрепленного на одном конце, и с диском на другом определяется равенством
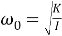
Общее решение однородной системы запишется в виде суммы главных колебаний вала с двумя жестко закрепленными дисками:
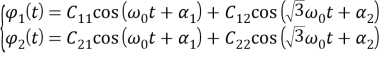
Таким образом, в ходе нашей работы мы получили решение дифференциального уравнения вынужденных колебаний однородной системы с двумя степенями свободы для внешней нагрузки, меняющейся со временем по гармоническому закону, а также определили собственную крутильную частоту вала, закрепленного на одном конце, и с диском на другом.
Литература:
1. Крутильные колебания [Электронный ресурс]. URL: https: //scask.ru/a_book_phis_t3.php?id=11
2. Управление измерениями. − М.: Альпина Паблишер, 2016, 226 с.
3. Верещагин В. И., Янович В. С., Ковальский Б. И. Методы контроля и результаты исследования состояния трансмиссионных и моторных масел при их окислении и триботехнических испытаниях: Монография / В. И. Верещагин, В. С. Янович, Б. И. Ковальский и другие, Красноярск: Сиб. федер. ун-т нефти и газа, 2017, 366 с.
4. Тювин А. В. Гравиинерциальные приборы, системы и комплексы. − М: МАИ, 2013, 37 с.
5. Сторожев В. В. Системотехника и мехатроника технологических машин и оборудования: Монография. − М: Дашков и К, 2016, 412 с.
6. Антошина Е. А. Надежность мехатронных и робототехнических систем. − Ковров: КГТА, 2017, 100 с.
7. Подураев Ю. В. Мехатроника: Основы, методы, применение. − М.: Ай Пи Ар Медиа, 2019, 261 с.

