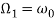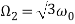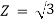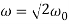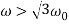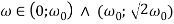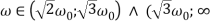В статье рассматривается моделирование вынужденных крутильных колебаний с двумя степенями свободы.
Ключевые слова: вынужденные крутильные колебания, вал с жестко закрепленными дисками, собственная частота колебаний, амплитуда, фаза.
В технике различного назначения (в том числе и военного) широко распространены крутильные колебания элементов конструкций и машин (например, вала), которые проявляются в периодически меняющейся деформации кручения. Причиной их возникновения является вариативность крутящего момента внешних сил. Периодичность изменения крутящего момента приводит к периодичности изменения угловой скорости вала.
Вал — это деталь машины, предназначенная для передачи крутящего момента и восприятия действующих сил со стороны расположенных на нем деталей [1]. Он представляет собой чередование упругих участков малой массы и участков, обладающих жесткостью, на которых закреплены тела большой массы. Каждое сечение вала имеет собственную степень неравномерности вращения, так как за равные промежутки времени участки вала поворачиваются на разные углы. Следовательно, они обладают различными угловыми скоростями. Если частота собственных колебаний системы с двумя степенями свободы совпадает с частотой изменения периодического крутящего момента внешних сил, то возникает резонанс. Это может привести к разрушению вала. Смоделируем амплитудно-частотные зависимости вынужденных крутильных колебаний системы с двумя степенями свободы.
В ряде работ [2, 3] авторы исследуют крутильные колебания валов с дисками, при этом рассматривают валы со свободными концами или с одним жестко закрепленным концом.
Используя дифференциальные уравнения Лагранжа, мы нашли общее решение однородной колебательной системы, состоящей из невесомого вала и двух массивных дисков с одинаковыми массами m и диаметрами D для случая жестко закрепленных дисков. В нашей задаче толщиной дисков ∆ ℓ по сравнению с длиной участков ℓ вала пренебрегли, то есть ℓ >> ∆ ℓ.
Общее решение однородной системы запишется в виде суммы главных колебаний вала с двумя жестко закрепленными дисками:
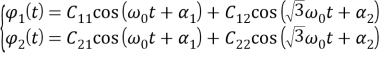
Найдем коэффициенты форм колебаний:
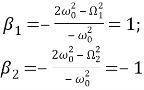
где
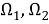
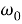
Общее решение однородного уравнения запишется в виде:
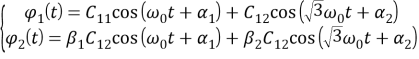
Используя уравнение Лагранжа, получим систему дифференциальных уравнений, описывающих вынужденные крутильные колебания:
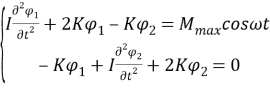
где
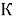
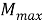
Найдем частное решение неоднородной системы дифференциальных уравнений (4) в виде гармонической зависимости от времени с частотой
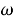
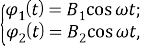
где
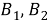
Подставляя функции (5) в систему (4), получим систему алгебраических уравнений для нахождения
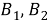
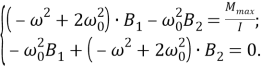
Амплитуды
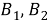
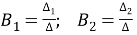
Запишем главный определитель и дополнительные определители:
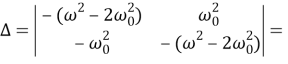
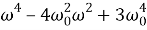
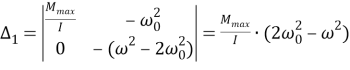
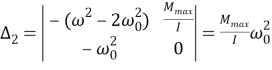
Введем угол кручения вала при статической нагрузке
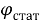
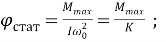
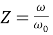
где
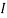
Используя выражения (8) - (11), перепишем равенства (7) в виде:
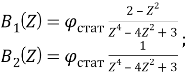
На рис. 1 представлены графические амплитудно-частотные зависимости
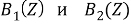
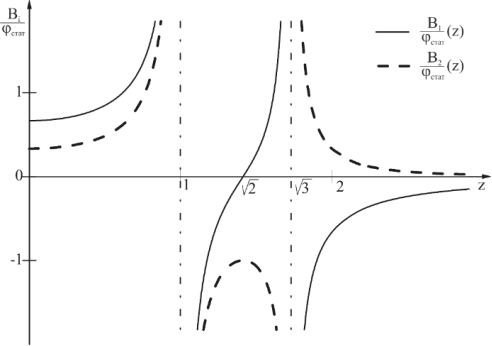
Рис.1. Амплитудно-частотные зависимости
Таблица 1
Анализ амплитудно-частотных зависимостей
|
Частота |
Результат |
|
|
Резонанс. |
|
|
Антирезонанс: амплитуда колебаний первого диска обращается в ноль. |
|
|
Амплитуда второго диска быстро убывает до нуля. |
|
|
Диски колеблются синфазно. |
|
|
Диски колеблются в противофазе. |
Как видно из рис.1 и таблицы 1, при возрастании внешней частоты могут возникать явление резонанса, антирезонанса, синфазные колебания или колебания, протекающие в противофазе.
Таким образом, в ходе нашей работы найдены собственные частоты вынужденных крутильных колебаний вала с дисками, жестко закрепленными на нем. Также получены и проанализированы временные зависимости амплитуд и фаз вынужденных крутильных колебаний вала с дисками, жестко закрепленными на концах, на основе модели описания колебательной системы с двумя степенями свободы.
Литература:
1. Вал [Электронный ресурс]. URL: https: // ru. wikipedia.jrg/wiki/Вал
2. Кадменский В. Г. Крутильные колебания вала с дисками// Сборник научных статей по материалам IV Всероссийской нпк «Академический Жуковские чтения». Воронеж: ВУНЦ ВВС «ВВА», 2017, с. 24–27.
- Кадменский В. Г., Илясов П. А. Крутильные колебаний вала с дисками в вязкой жидкости// Сборник научных статей по материалам IV Всероссийской нпк «Академический Жуковские чтения». Воронеж: ВУНЦ ВВС «ВВА», 2017, с. 181–186.