Анализ влияния кризиса 2020 года на рынок вторичного жилья



В экономических исследованиях часто встает задача дать количественное описание между экономическими переменными. Для этого в эконометрике широко используются методы статистики. Прежде всего, это связано с методами регрессии и корреляции. В зависимости от количества факторов, которые включают в уравнение регрессии, используют парную или множественную линейную регрессии. Парную регрессию используют в том случае, если имеется доминирующий фактор, который используется в качестве объясняющей переменной, а множественную, если не удается обеспечить равенство всех прочих условий для оценки влияния одного исследуемого фактора.

В данный момент в стране начинается международный кризис, который вызван несколькими причинами: коронавирус COVID-19 и снижение стоимости нефти [2; 3, c. 5]. В сфере первичной недвижимости себестоимость строительства будет расти, потому что часть строительных материалов приобретается за рубежом за доллары. Анализируя мнения экспертов можно сказать, что в краткосрочной перспективе возможен всплеск на рынке недвижимости, потому что люди будут пытаться сохранить свои средства, однако в долгосрочной перспективе покупательская способность уменьшиться [5, 6, 7]. На апрель 2020 г. резкого снижения цен не прогнозируется ввиду того, что в стране введен режим самоизоляции и продавцам не нужен повышенный спрос на квартиру ввиду того, что они не смогут ее показать и оформить документы на продажу. Анализ рынка недвижимости важен потому, что он оказывает влияние на рыночные отношения и участвует в экономических процессах. В стоимости квартир содержится информация о насыщенности данного рынка, покупательной способности населения и другая.

В данной работе исследуем зависимость стоимости квартиры от ее площади по данным на январь 2020 г. и сравним полученные показатели с данными на первую декаду апрель 2020 г. по городу Иркутску. Проанализируем, как изменилась зависимость цены от площади на вторичном жилье с учётом факторов, о которых говорилось выше. Нам необходимо исследовать зависимость стоимости квартиры от ее площади. Для этого воспользуемся моделью парной линейной регрессии. Для исследования нам необходимо выбрать данные, которые будем анализировать. Для анализа возьмем 28 наблюдений за январь 2020 (рис. 1) и за первую декаду апреля 2020 г. (рис. 2.) по городу Иркутску с сайта Domofond.ru. Отметим, что варьирование признака должно быть не более 35 % [4, c.70].

Рис. 1. Данные за январь 2020 г.

Рис. 2. Данные за апрель 2020 г.

В данном случае Y — результативный фактор (стоимость квартиры в млн рублей), а X — количественный фактор (площадь квартиры в

). Решение задачи выполним с помощью MS Excel. В первую очередь с помощью встроенной статистической функции «ЛИНЕЙН» определим параметры выборочного уравнения линейной регрессии . В результате мы получим следующую таблицу для первого набора данных (рис. 3) и для второго набора данных (рис. 4.). На основании полученных данных можем составить выборочные уравнения регрессии:

;

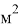
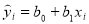
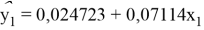
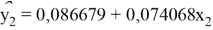
(0,0067) (0,3655) (0,3074) (0,0057)

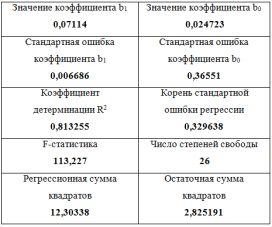
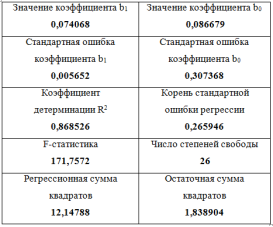
Рис. 3, 4. Данные за январь 2020 г. и апрель 2020 г.

Теперь с помощью инструмента анализа данных «Регрессия» получим результаты регрессионной статистики, дисперсионный анализ, доверительные интервалы, остатки и графики подбора линии регрессии, остатков. Получаем следующие результаты для первого набора данных (рис. 5 ) и для второго (рис. 6). Обратим внимание на то, что p-значение для t-критерия в обоих случаях меньше 0,05. Если бы мы получили результат, где эти значения были бы больше 0,05, нам было бы необходимо строить новую модель, несмотря даже на то, что глобальные значения для исходных вероятностей указывают на статистическую значимость. Коэффициенты регрессии не должны быть равны нулю, только в этом случае мы можем использовать модель. Для каждой независимой переменной коэффициент регрессии и связанный с ним доверительный интервал не должен включать в себя 0. Включение этой переменной может негативно отразиться на общую значимость модели. В нашем примере доверительные интервалы не включают в себя 0, поэтому продолжаем исследовать модели.

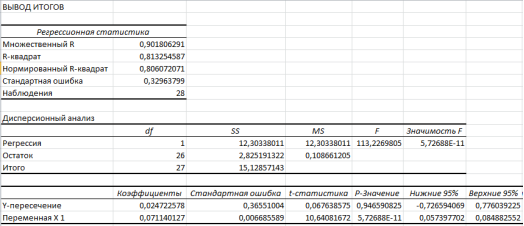
Рис. 5. Для данных за январь 2020 г.

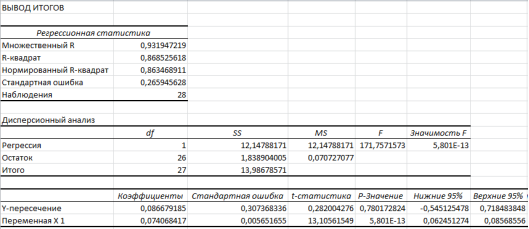
Рис.6. Для данных за апрель 2020 г.

Также для анализа построим графики остатков для первого набора данных (рис. 7, рис. 8) и для второго (рис. 9, рис. 10), которые позволят визуально проконтролировать качество подбора модели и отсутствие закономерности в остатках. Для более наглядного представления результатов добавим линию тренда.

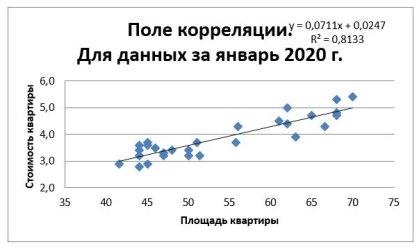
Рис.7

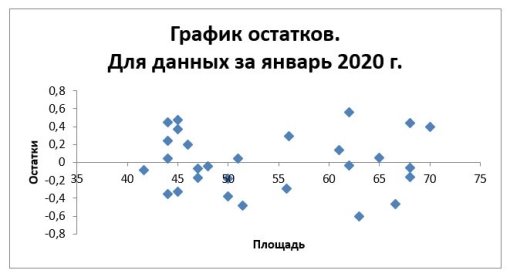
Рис. 8

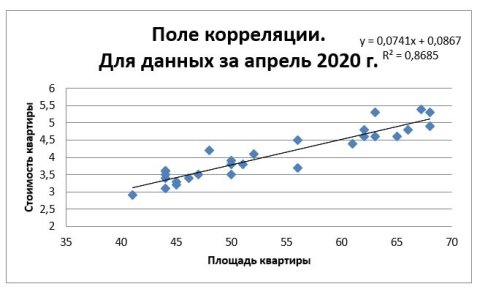
Рис. 9

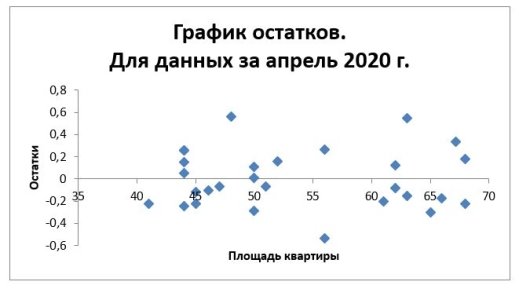
Рис. 10

Анализируя графики поля корреляции можно сказать, что форма связи: линейная положительная, выбросов на графиках нет, соответственно они не повлияют на точность модели.

Коэффициент детерминации указывает на то, что соответствующее уравнение регрессии на 81 % объясняется уравнением регрессии (вариацией величины X) для первого набора данных и на 87 % для второго. Модель, построенная на первом наборе данных, является менее точной, чем на второй. Таким образом, зависимость стоимости квартиры от площади высокая, но для первого набора данных сторонние факторы, которые мы не рассматриваем, играли более важную роль.

Необходимо исследовать гетероскедастичность остатков. Гетероскедастичность остатков — это свойство остатков, которое заключается в том, что их дисперсии или разбросы для каждого фиксированного Х являются неоднородными или неодинаковыми. Наличие гетероскедастичности в регрессионной модели может привести к негативным последствиям [1]:

1. Оценки уравнения нормальной линейной регрессии остаются несмещенными и состоятельными, но при этом теряется эффективность;
2. Появляется большая вероятности того, что оценки стандартных ошибок коэффициентов регрессионной модели будут рассчитаны неверно, что, в конечном счете, может привести к утверждению неверной гипотезы о значимости регрессионных коэффициентов и значимости уравнения регрессии в целом.

Гетероскедастичность можно исправить применением обобщенного метода наименьших квадратов [4, c.192]. Наличие гетероскедастичности в остатках регрессии можно проверить с помощью [4, c.193–201]:

– Графического анализа остатков;

– Теста Гольдфельда-Квандта;

– Теста ранговой корреляции Спирмена;

– Теста Парка;

– Теста Уайта.

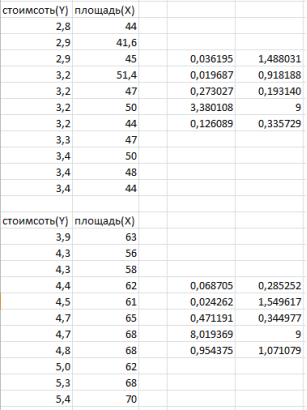
Рис.11. Для данных за январь 2020 г.

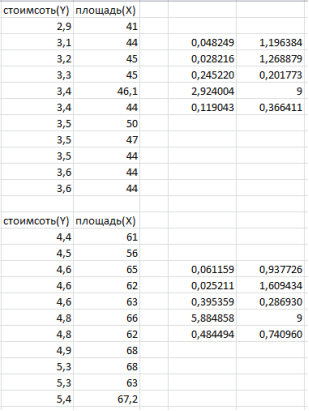
Рис. 12. Для данных за апрель 2020 г.

С помощью теста Гольдфельда-Квандта исследуем гетероскедастичность остатков. Отсортируем наши выборки по переменной X и уберем c=6 средних элементов, получим две подвыборки (рис. 11) для первого набора данных и для второго набора (рис. 12). Выберем значения корня стандартной ошибки регрессии и путем возведение этих числе в квадрат найдем стандартные ошибки регрессии для первого набора данных: , , для второго: , .

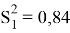
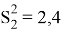
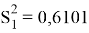
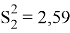
H ₀ выдвигаем нулевую гипотезу, которая заключается в отсутствии гетероскедастичности. Рассчитаем значение критерия Фишера по формуле F ₁ = 2,85, F ₂ =1,6109. Квантиль 3,1789

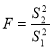
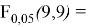
Поскольку для наборов данных, мы отвергаем нулевую гипотезу и с вероятностью 95 % утверждается, что гетероскедастичность остатков является ложной. Имеет место гомоскедастичность.

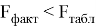
Рассчитаем прогнозное значение результата, если значение фактора увеличится на 5 % от его среднего уровня. Определим доверительный интервал прогноза для уровня значимости =0,05.

53,87, ; 53,65, .

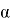
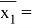
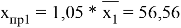
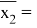
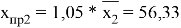
Подставим в выборочное уравнение регрессии: , прогнозное значение x:

,

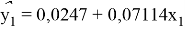
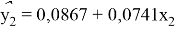
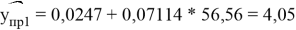
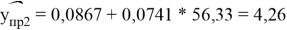
Из этого делаем вывод, что по данным на январь 2020 года, если в среднем квартира имеет площадь 56,56 , то ожидаемая стоимость в среднем 4,05 млн. руб. А для данных на апрель 2020 года, если в среднем квартира имеет площадь 56,33 м ² , то ожидаемая стоимость 4,26 млн. руб. Средняя цена за 1 м ² по данным за январь составляет 71605 руб., а в апреле 75625 руб., таким образом, цена за 1 м ² выросла на 5,6 %.

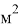
Найдем дисперсию прогноза, для того чтобы оценить его точность, отметим, что чем меньше диспепсия, тем точнее прогноз: Подставив вместо её несмещённую оценку , получим выборочную исправленную дисперсию рассматриваемой случайной величины. Несмещенные оценки для наборов данных: ,

.

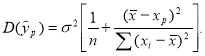
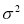
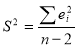
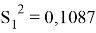
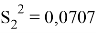
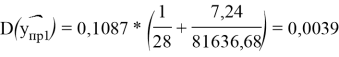
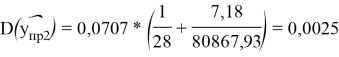
То есть точность прогноза для данных за апрель выше. Однако дисперсия не равна нулю, соответственно в прогнозе есть небольшие отклонения.

Рассчитаем интервальный прогноз среднего значения по уравнению регрессии. Доверительный интервал для М(Y/X=x _р ) имеет вид: Подставив значения в формулу, получим следующий интервал для первого набора данных (4,04; 4,06) и для второго набора данных (4,25; 4,26).

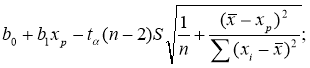
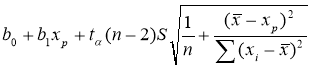
Из этого делаем вывод, что если в среднем квартира имеет площадь 56,56 (для первого набора данных) и 56,33

(для второго набора данных), то ожидаемая стоимость находится в интервалах, приведенных выше для каждого набора данных.

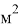
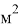
Сделаем интервальный прогноз индивидуальных значений зависимой переменной.

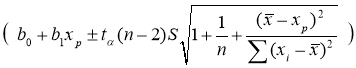
Он определяет границы, за пределами которых могут оказаться не более 100α % точек наблюдений при Х=х _р . Данный доверительный интервал шире доверительного интервала для условного математического ожидания. Получим следующий интервал для первого набора данных (4,13; 4,38) и для второго (3,86; 4,24).

Проведя данное исследование, мы смогли с помощью модели парной линейной регрессии при помощи статистических методов установить и количественно измерить связи между экономическими процессами и явлениями на основании полученных данных. Также интерпретировали и использовали полученные результаты для сравнения и анализа стоимости вторичного жилья на январь 2020 года и на апрель 2020 года в городе Иркутске. Проанализировав полученные данные, сравнив их с мнениями экспертов, можем сказать, что кризис, который начался в стране, вызванный коронавирусом COVID-19 и снижением стоимости нефти, повлиял на стоимость вторичного жилья в городе Иркутске. Стоимость вторичного жилья на апрель 2020 года, по данным исследования, выросла на 5,6 % по сравнению с январем 2020 года.

Литература:

1. Универ: [сайт]. — URL: http://univer-nn.ru/ekonometrika/geteroskedastichnost/ (дата обращения: 16.04.2020). — Текст: электронный.
2. Всемирный банк: [сайт]. — URL: https://www.vsemirnyjbank.org/ru/news/press-release/2020/04/23/most-commodity-prices-to-drop-in-2020-as-coronavirus-depresses-demand-and-disrupts-supply (дата обращения: 23.04.2020). — Текст: электронный.
3. Центр энергетики Московской школы управления СКОЛКОВО: [сайт]. — URL: https://energy.skolkovo.ru/downloads/documents/SEneC/Research/SKOLKOVO_EneC_COVID19_and_Energy_sector_RU.pdf (дата обращения: 22.04.2020). — Текст: электронный.
4. Елисеева И. И., Курышева С. В., Костеева Т. В. и др. Эконометрика. — М.: Финансы и статистика, 2007. — 576 с.
5. РБК: [сайт]. — URL: https://realty.rbc.ru/news/5e8184319a794784f6672a20 (дата обращения: 08.04.2020). — Текст: электронный.
6. РБК: [сайт]. — URL: https://realty.rbc.ru/news/5e81cd3a9a7947ac8aaf5628 (дата обращения: 08.04.2020). — Текст: электронный.
7. РБК: [сайт]. — URL: https://realty.rbc.ru/news/5e6a1e8b9a79470b84911820 (дата обращения: 08.04.2020). — Текст: электронный.