Анализ данных генной экспрессии требует подходящих инструментов для хранения и использования, соответствующих объемом данных; одной из последних и полезных технологий является технология микрочипов, которые позволяют хранить данные в единой матрице. В настоящее время данная технология может генерировать огромное количество информации о генной экспрессии. Эта информация должна быть статистически обработана и проанализирована для выявления тех генов, которые полезны для диагностики и прогноза конкретных заболеваний. Мы рассмотрим возможность применения игровых теоретических инструментов для анализа данных экспрессии генов, аксиоматически охарактеризуем эти инструменты, используя свойства с генетической интерпретацией.
Ключевые слова: коалиционная игра, значение Шепли, Индекс Банзафа, MSC-вектор, CGM-вектор, метод равных доходов, экспрессия гена, патогенез.
Как известно, белки являются структурными составляющими клеток и тканей и могут действовать при необходимости как ферменты для реакций в биологических системах. Большинство генов содержат информацию для изготовления конкретного белка. Она кодируется в генах с помощью дезоксирибонуклеиновой кислоты (ДНК). С помощью технологии микрочипов можно выяснить роль отдельных генов или групп генов в появлении болезни. В практическом отношении применение микрочипов уже сегодня позволяет решать следующие задачи:
– точная постановка диагноза и выявление новых подтипов заболевания
– прогнозирование течения болезни и клинического исхода, выявление генов, вовлеченных в патогенез онкогематологических заболеваний
– разработка и создание более простых и дешевых диагностических тестов, в том числе и на основе технологии микрочипов (микрочипы, содержащие пробы на десятки или сотни генов вместо десятков и сотен тысяч).
В статье [3] V. Fragnelli и S. Moretti рассматривают игру с генами для классификации образцов в определенные классы (например, класс образцов из нормальных тканей и из тканей больных раком). В некоторых численных примерах авторы используют вектор Шепли для вычисления генов с высоким влиянием в вычислении образцов.
В статье [4] дана аксиоматическая характеристика значения Шепли с помощью пяти свойств, подходящих для генетической интерпретации этого индекса.
Математическая постановка
Пусть G= {1, 2,..., n} набор из n генов, SR={1, 2,..., r} множество образцов клеток из здоровых тканей, и SD={1, 2,..., d} множество образцов из тканей, представляющих интерес. Цель состоит в том, чтобы сопоставить каждому образцу j![]() SD∪SR профайл экспрессии
SD∪SR профайл экспрессии ![]() G. Набор данных представлен в форме двух матриц экспрессии:
G. Набор данных представлен в форме двух матриц экспрессии: ![]() и
и ![]() (где индекс представляет столбец, являющийся профайлом экспрессии образца j).
(где индекс представляет столбец, являющийся профайлом экспрессии образца j).
Характеристическая функция будет вычисляться по формуле:v (T) = ![]() , где |SD|-мощность множества больных образцов, а |Q(T)|- мощность множества:
, где |SD|-мощность множества больных образцов, а |Q(T)|- мощность множества: ![]()
Вектор ![]() , где
, где![]() будем называть анормальным профайлом экспрессии. В виде отображения m выразим дискриминантный метод. Существуют различные дискриминантный методы. Например, наивный метод: где 1- аномально, 0- нормально выраженный ген:
будем называть анормальным профайлом экспрессии. В виде отображения m выразим дискриминантный метод. Существуют различные дискриминантный методы. Например, наивный метод: где 1- аномально, 0- нормально выраженный ген:
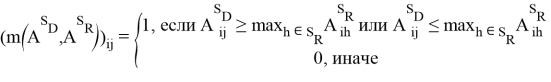
Также можно воспользоваться более консервативным методом. Для каждого ![]()
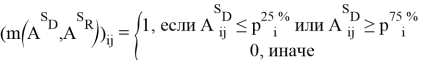
Где ![]() и
и ![]() являются 25-ым и 75-ым процентилями распределения экспрессии гена
являются 25-ым и 75-ым процентилями распределения экспрессии гена ![]() в соответствующей матрице экспрессии
в соответствующей матрице экспрессии ![]()
Возможные методы решения
В настоящее время для данной задачи существует несколько возможных методов решения: вектор Шепли, индекс Банзафа, MSC-вектор, CGM-вектор, метод равных доходов. Рассмотрим каждый из них.
Одно из самых популярных решений — вектор Шепли.
Для подсчета вектора необходимо ввести понятие личного вклада каждого гена в образование генотипа, определяемого формулой: m(v, S)= v(S)-v(S\{i}).
Полученные нами данные позволяют ввести вектор Шепли:
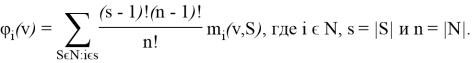
Другое решение кооперативной игры — индекс Банзафа:
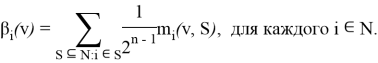
MSC-вектор[5]— принцип оптимальности, определяющий выигрыш игрока по следующей формуле:
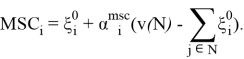
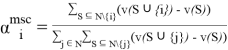 и
и ![]()
CGM-вектор[6] — принцип оптимальности, основанный на r- значении игры и вычисленный по формуле:
![]()
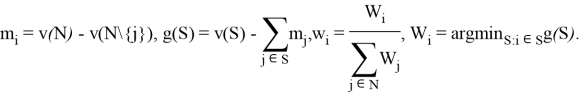
Метод равных доходов [7]- вектор, который обеспечивает как можно более высокую относительную прибыль среди игроков:
![]()
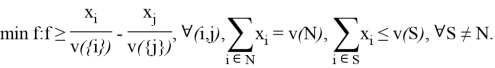
Аксиоматическая характеристика возможных методов решения с помощью свойств, подходящих для генетической интерпретации.
Для того чтобы охарактеризовать решения с помощью свойств с генетической интерпретацией, определение партнерства генов играет основную роль.
Определение 1. Пусть v ![]() MN. Коалиция S
MN. Коалиция S ![]() 2N\ {
2N\ {![]() } такой, что для каждого T⊊S и каждого R ⊆ N \ S: v (R ∪ T) = v (R) — это партнерство генов в игре микроматрицы v.
} такой, что для каждого T⊊S и каждого R ⊆ N \ S: v (R ∪ T) = v (R) — это партнерство генов в игре микроматрицы v.
Значение v(S) партнерства генов S-максимальное среднее количество появлений опухоли. Пусть v![]() M. Максимальное партнерство S ∈
M. Максимальное партнерство S ∈ ![]() \ {∅} в v является максимальным подмножеством N с возможностью быть партнерством в v. Обозначим через P(v) множество всех максимальных партнерств в v. Отметим, что из определения 1 следует, что все коалиции одного игрока являются партнерствами в v. Набор максимальных партнерств в v образует разделение N. Здесь мы рассмотрим некоторые интересные свойства для решений игр с микрочипами, которые связаны с концепцией партнерства генов. Пусть F: MN→ IRN — решение на классе игр с микрочипами.
\ {∅} в v является максимальным подмножеством N с возможностью быть партнерством в v. Обозначим через P(v) множество всех максимальных партнерств в v. Отметим, что из определения 1 следует, что все коалиции одного игрока являются партнерствами в v. Набор максимальных партнерств в v образует разделение N. Здесь мы рассмотрим некоторые интересные свойства для решений игр с микрочипами, которые связаны с концепцией партнерства генов. Пусть F: MN→ IRN — решение на классе игр с микрочипами.
Свойство 1. Пусть (N,v) ∈ ![]() Решение F имеет Рациональность Партнерства (Partnership Rationality), если
Решение F имеет Рациональность Партнерства (Partnership Rationality), если ![]() для каждого S ∈
для каждого S ∈ ![]() \ {∅} такого, что S является партнерством генов в игре (N,v).
\ {∅} такого, что S является партнерством генов в игре (N,v).
Свойство 2. Пусть (N,v) ∈ ![]() Решение F обладает свойством вероятности партнерства (Partnership Feasibility), если
Решение F обладает свойством вероятности партнерства (Partnership Feasibility), если ![]() для каждого такого S ∈
для каждого такого S ∈ ![]() \ {∅}, что S является партнерством генов в игре (N,v).
\ {∅}, что S является партнерством генов в игре (N,v).
Свойство 3. Пусть (N,v) ∈ ![]() Решение F обладает свойством монотонности партнерства (Partnership Monotonicity), если
Решение F обладает свойством монотонности партнерства (Partnership Monotonicity), если ![]() для каждого i ∈ S и каждого j ∈ T, где S, T ∈
для каждого i ∈ S и каждого j ∈ T, где S, T ∈ ![]() \ {∅}партнерства генов в (N,v), такой, что S ∩ T = ∅, v (S) = v (T), v (S ∪ T) = v (N), |S|≤|T|.
\ {∅}партнерства генов в (N,v), такой, что S ∩ T = ∅, v (S) = v (T), v (S ∪ T) = v (N), |S|≤|T|.
Свойство 4. Пусть ![]() . Решение F обладает свойством равного деления (Equal Splitting), если
. Решение F обладает свойством равного деления (Equal Splitting), если 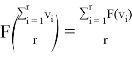 .
.
Определение 2. Нулевым геном игры (𝑁, 𝑣) будем называть ген 𝑖 ∈ 𝑁 такой что 𝑣(𝑆 ∪ 𝑖) = 𝑣(𝑆) для каждой коалиции 𝑆 ⊆ 𝑁\{𝑖}
Свойство 5. Пусть v, w ∈ ![]() . Решение F, удовлетворяет свойству нулевого игрока (Null Player), если для каждого нулевого игрока i ∈ N: Fi(v) = 0.
. Решение F, удовлетворяет свойству нулевого игрока (Null Player), если для каждого нулевого игрока i ∈ N: Fi(v) = 0.
В статье [8] представлено доказательство утверждения, что значение Шепли удовлетворяет свойствам PM, PR, PF. В этой же статье можно найти доказательство следующей теоремы:
Теорема 1. Пусть дано конечное множество N. Значение Шепли на классе MN игр с микрочипами — это уникальный индекс релевантности, который удовлетворяет PR, PF, PM, ES и NP.
Таким образом, можем сделать вывод, что кооперативная теория игр может применяться для микрочиповых игр, например вектор Шепли и индекс Банзафа.
Далее было проверено, удовлетворяют ли MSC-вектор, CGM-вектор и метод равных доходов свойствам PR,PF,PM,ES и NP.
Рассмотрим MSC-вектор.
А) Для каждого S![]() S- максимальное партнерство по v. Так как v- монотонна и MSC- вектор находится в C- ядре, то справедлива запись:
S- максимальное партнерство по v. Так как v- монотонна и MSC- вектор находится в C- ядре, то справедлива запись: ![]()
Так как MSC-вектор является одноточечным, то это решение эффективно. А из этого следует: ![]() значит, аксиома PF выполняется.
значит, аксиома PF выполняется.
Б) Исходя из того, что это вектор, можем умножить на скаляр. Из чего следует однородность, а значит, справедлива запись: 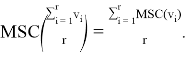 Для MSC-вектора свойство ES выполняется.
Для MSC-вектора свойство ES выполняется.
В) Для доказательства удовлетворения MSC- вектора аксиоме PR, вспомним, что v- монотонна и MSC-вектор принадлежит C-ядру, а значит, верна запись: ![]() Таким образом, для MSC- вектора выполняется аксиома PR.
Таким образом, для MSC- вектора выполняется аксиома PR.
Г) Теперь рассмотрим, выполняется ли для MSC-вектора аксиома болвана: пусть вклад i-ого игрока в коалицию: ![]() , то есть
, то есть ![]()
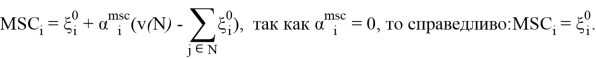
По условию индивидуальной рациональности: ![]() . О равенстве
. О равенстве ![]() нулю однозначно сложно сказать. Было проведено исследование свойств одноточечных решений и их применения для исследований. Вектор MSC в общем случае не удовлетворяет аксиоме NP. Записав условия на компоненты вектора X:
нулю однозначно сложно сказать. Было проведено исследование свойств одноточечных решений и их применения для исследований. Вектор MSC в общем случае не удовлетворяет аксиоме NP. Записав условия на компоненты вектора X: ![]() , можно сделать вывод, что данный вектор будет удовлетворять аксиоме NP, в том случае, если
, можно сделать вывод, что данный вектор будет удовлетворять аксиоме NP, в том случае, если ![]()
Рассмотрим метод равных доходов: ![]()
А) Пусть вклад i-ого игрока в коалицию: ![]() , то есть
, то есть ![]() Это возможно, при
Это возможно, при ![]() Условие коалиционной рациональности:
Условие коалиционной рациональности: ![]() Таким образом, метод равных доходов удовлетворяет условию NP, при
Таким образом, метод равных доходов удовлетворяет условию NP, при ![]()
Б) Так как v- монотонна и EPM находится в С-ядре, то верно: ![]()
Данное решение является вектором, а значит одноточечно. Из всего перечисленного следует эффективность: ![]()
Следовательно, аксиома PF выполняется для метода равных доходов.
В)Для доказательства удовлетворения метода равных доходов аксиоме PR, вспомним, что v- монотонна и данное решение принадлежит C-ядру, а значит, верна запись: ![]() Таким образом, для EPM выполняется аксиома PR.
Таким образом, для EPM выполняется аксиома PR.
Г) Исходя из того, что это вектор, можем умножить на скаляр. Из чего следует однородность, а значит, справедлива запись: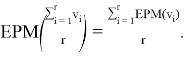 Для EPM свойство ES выполняется.
Для EPM свойство ES выполняется.
Рассмотрим CGM- вектор: ![]()
А) Так как это вектор, можем умножить на скаляр, следовательно, данное решение удовлетворяет свойству однородности, а значит, справедлива запись: 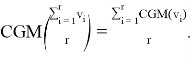 Для CGM свойство ES выполняется.
Для CGM свойство ES выполняется.
Б) Рассмотрим CGM-вектор. Для каждого S![]() S- максимальное партнерство по v. Так как v- монотонна и CGM- вектор находится в C- ядре, то справедлива запись:
S- максимальное партнерство по v. Так как v- монотонна и CGM- вектор находится в C- ядре, то справедлива запись: ![]() Так как CGM-вектор является одноточечным, то это решение эффективно. А из этого следует
Так как CGM-вектор является одноточечным, то это решение эффективно. А из этого следует ![]() значит, аксиома PF выполняется.
значит, аксиома PF выполняется.
В) Для доказательства удовлетворения CGM- вектора аксиоме PR, вспомним, что v- монотонна и CGM-вектор принадлежит C-ядру, а значит, верна запись: ![]() Таким образом, для CGM- вектора выполняется аксиома PR.
Таким образом, для CGM- вектора выполняется аксиома PR.
Г) Теперь рассмотрим, выполняется ли для CGM-вектора аксиома болвана: пусть вклад i-ого игрока в коалицию: ![]() , то есть
, то есть ![]()
![]()
То есть для того, чтобы CGM- вектор удовлетворял аксиоме болвана должно выполняться: ![]() или
или 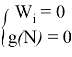
Выводы
Проведённые исследования показали, что значение Шепли на классе MN игр с микрочипами — это уникальный индекс релевантности, который удовлетворяет PR, PF, PM, ES и NP. Таким образом, можем сделать вывод, что кооперативная теория игр может применяться для микрочиповых игр, например вектор Шепли и индекс Банзафа. Другие приведенные методы MSC-вектор, CGM-вектор и метод равных доходов в общем случае не удовлетворят свойствам PR,PF,PM,ES и NP. Также в данной работе представлены условия, при выполнении которых вышеупомянутые методы можно реализовывать для задач генетики.
Заключение
В данной работе были рассмотрены различные методы теории игр и аксиоматическая характеристика возможных методов решения с помощью свойств, подходящих для генетической интерпретации. Было проведено исследование свойств одноточечных решений, а именно подробное изучение факта удовлетворения свойствам, обеспечивающим возможность применения в генетике.
Литература:
- статья Gupta S., Manubhai K. P., Kulkarni V., Srivastava S. An overview of innovations and industrial solutions in Protein Microarray Technology // Proteomics. 2016. 16:1297–1308.
- Moretti, S., Vasilakos, Athanasios V. «An overview of recent applications of Game Theory to bioinformatics».
- «A game theoretical approach to the classification problem in gene expression data analysis» V. Fragnelli и S. Moretti.
- Stefano Moretti, Fioravante Patrone, Stefano Bonassi. ‘The class of microarray games and the relevance index for genes’.
- Jaeger J, Spang R, 2006.
- Smyth, G. K., Yang, Y.-H., Speed, T. P. «Statistical issues in cDNA microarray data analysis»
- Dhammika Amaratunga & Javier Cabrera “Exploration and Analysis of DNA Microarray and Protein Array Data”.
- «A game theoretical approach to the classification problem in gene expression data analysis» V. Fragnelli и S. Moretti.

