В статье рассматривается беспоисковая система адаптивного управления линейным одноканальным объектом с запаздыванием на множестве состояний функционирования. Данная система построена на основе критерия гиперустойчивости. Имитационное моделирование проводилось в среде Simulink.
Ключевые слова: адаптивная система управления, гиперустойчивость, динамический корректор, запаздывание по состоянию, эталонная модель.
Адаптивное управление в настоящее время позволяет решать задачи управления различной сложности, одной из актуальных проблем в этой области является управление динамическим объектом с запаздыванием на множестве состояний функционирования, т. е. в ходе движения объекта управления допускается резкое изменение его модели динамики под воздействием внешней среды или в результате изменения условий функционирования системы.
Математическое описание
Пусть объект управления имеет следующее математическое описание:
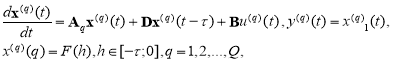(1)
где q = 1,2,…,Q — ограниченное количество интервалов времени; x(q)T(t) = [x1(q)(t) x2(q)(t) x3(q)(t)] — вектор состояния на интервале времени q; = const>0 — известное временное запаздывание; x(q)(h) — непрерывная и ограниченная во времени начальная функция; u(q)(t) — скалярное управление; y(q)(t) — вектор выхода; B — вектор управления; Aq и D матрицы размера nx n представленные в виде:
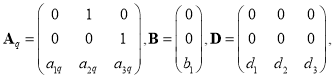(2)
функционирующие в условиях априорной неопределенности:
Aq=Аq(), B=B(),D=D(),, (3)
где — набор неизвестных параметров принадлежащих некоторому множеству ; в явном виде эти условия представляют собой набор двухсторонних неравенств:
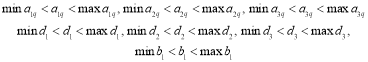(4)
Уравнению (1) соответствует передаточная функция на интервале времени q вида:
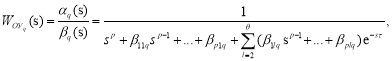(5)
где WОУq(s) — передаточная функция объекта управления (ОУ); αq(s) — гурвицев полином; βq(s) — квазиполином с произвольным расположением корней; p — степень квазиполинома.
Динамический корректор имеет следующее математическое описание:
(6)
где WДК(s) — передаточная функция динамического корректора, δ(s), γ(s) — соответствующие гурвицевы многочлены, T*>0 — числовой параметр.
Математическое описание эталонной модели имеет вид:
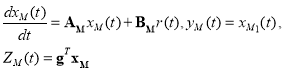(7)
Опираясь на работу Ерёмина Е. Л. [4], в которой он показал, что при последовательном соединении динамического корректора и объекта управления, а также, при выполнении условия L-диссипативности, которое заключается в выборе параметра T*, из условия:
(8)
где T*+ определяется меньшим значением из:
(9)
где βm1 и βm2 — коэффициенты многочлена эталонной модели, k — степень динамического корректора, математическое описание объекта управления примет вид:
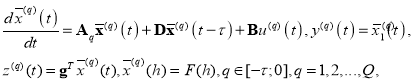(10)
где 
— оценки вектора пространства состояний, z(q)(t) — обобщенный выход, gT –вектор выхода, формируемый с коэффициентами gi — значения которых вычисляются из соотношения:
(11)
Очевидно, что существуют постоянные векторы C1, С2 и число K0 что для объекта управления (10) и эталонной модели (7) будут выполнятся условия структурного согласования:
(12)
Введем ошибку рассогласования сигнала в виде:
(13)
Постановка задачи
Для объекта управления (10), функционирующего в условиях априорной неопределенности необходимо построить замкнутую систему управления с помощью адаптивного регулятора, имеющего следующую структуру:
(14)
где K(t),C1(t) и С2(t) настраиваемые коэффициенты, алгоритмы настройки которых имеют вид:
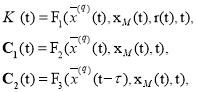(15)
Задачу необходимо решить таким образом, чтобы реакция системы (10), (12), (13), (14) на задающее воздействие r(t), по окончании процесса адаптации совпадала с динамикой эталонной модели вида (7), а также выполнялись следующие целевые условия:
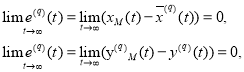(16)
и условия адаптации:
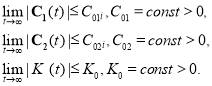(17)
Синтез алгоритмов контура адаптации.
Принимая ошибку в виде (13) получим эквивалентное математическое описание системы в виде:
(18)
(19)
где (18) — линейная стационарная часть; (19) — нелинейная нестационарная часть.
Согласно работе [1,2], если задать алгоритмы адаптации уравнениями:
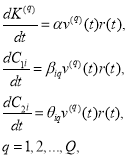(20)
где α, βi и θi — соответствующие числа. А вектор g будет удовлетворять частотному неравенству:
(21)
то будет разрешимо интегральное неравенство:
(22)
При q = 1 = Q система управления будет асимптотически гиперустойчивой в силу выполнения предельного соотношения:
(23)
Согласно [9] для tq-1≤ t < tq, q = 1,2,…,Q требуется модифицировать алгоритмы адаптации, тогда процесс адаптации будет завершатся за конечное время Tq, что позволит получить адаптивную систему управления, отвечающую целевым условиям и условиям адаптации. Модифицированные алгоритмы адаптации имеют следующий вид:
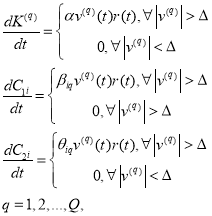(24)
Имитационное моделирование
Рассматривается объект управления с передаточной функцией:
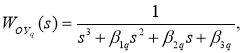(25)
где коэффициенты передаточных функций WОУq поэтапно принимают кусочно-постоянные значения на интервалах времени:
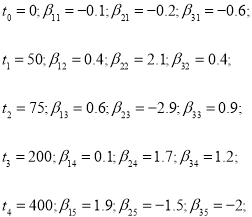(26)
Параметры динамического корректора были заданы в виде:
(27)
Постоянное временное запаздывание =2 сек.
Задающее воздействие задано в соответствии с динамикой объекта управления и эталонной моделью и имеет вид:
(28)
Для обеспечения вещественности и строгой положительности передаточной функции вида (25) вектор g был выбран следующим образом:
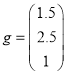(29)
Параметры эталонной модели представлены в виде:
(30)
Матрица запаздывания задана в виде:
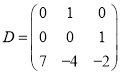(31)
При настройки адаптивного регулятора, были подобраны следующие коэффициенты:
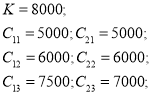(32)
На рисунке 1 представлена ошибка рассогласования динамики объекта управления и эталонной модели рассматриваемой системы, как видно из графика, ошибка не превышает 3 %, что говорит о хорошей работоспособности контура адаптации.
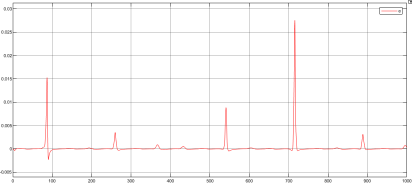
Рис. 1. Ошибка рассогласования ОУ и ЭМ
На рисунках 2 и 3 изображена динамика объекта управления и эталонной модели. Исследуя график, можно сделать вывод, что динамика ОУ и ЭМ практически совпадают.
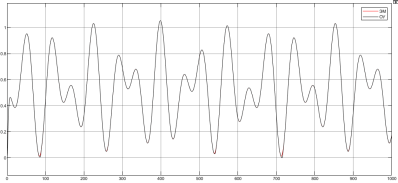
Рис. 2. Динамика ОУ и ЭМ
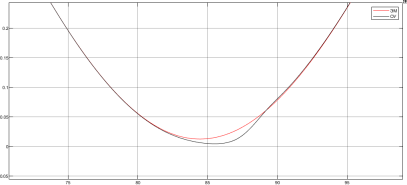
Рис. 3. Динамика ОУ и ЭМ на интервале времени 70–100 с.
На рисунке 4 показаны настройки адаптивного регулятора, рассматривая график можно сделать вывод, что выполняется условие (20), ошибка стремится к константе.
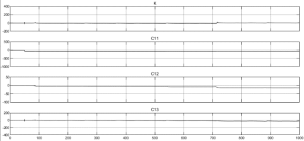
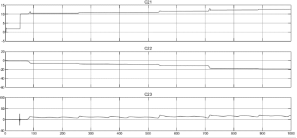
Рис. 4. Настройка коэффициентов регулятора
Литература:
- Еремин Е. Л., Цыкунов А. М. Синтез адаптивных систем управления на основе критерия гиперустойчивости. — Бишкек: Илим, 1992.
- Еремин Е. Л. Алгоритмы адаптивной системы управления с явно-неявной эталонной моделью для строго минимально-фазового объекта — Информатика и системы управления. — 2004. — № 2 (8). — С. 157–166.
- Еремин Е. Л. Построение адаптивных систем с запаздыванием по управлению на основе эталонного упредителя — Информатика и системы управления. — 2005. — № 1 (9). — С. 122–128.
- Еремин Е. Л. L-диссипативность гиперустойчивой системы управления при структурном возмущении // Информатика и системы управления. — 2006. — № 2 (12). — С. 94–101.
- Еремин Е. Л., Теличенко Д. А. Алгоритмы адаптивной системы с запаздыванием по управлению в схеме с расширенной ошибкой и эталонным упредителем // Мехатроника, автоматизация, управление. — 2006. — № 6. — С. 9–16
- Еремин Е. Л., Теличенко Д. А., Шеленок Е. А. Циклический режим в системе робастного управления манипулятором Барретта // Вестник Тихоокеанского государственного университета. — 2010. — № 3. — С. 23–32.
- Еремин Е. Л., Кван Н. В., Семичевская Н. П. Робастное управление нелинейными объектами с наблюдателем полного порядка и быстродействующей эталонной моделью // Мехатроника, автоматизация, управление. — 2010. — № 5. — С. 2–6.
- Еремин Е. Л., Шеленок Е. А. Имитационное моделирование адаптивной системы управления одноканальным объектом с запаздыванием нейтрального типа и входным насыщением //Датчики и системы. — 2017. — № 10 (218). — С. 3–9.
- Еремин Е. Л. Адаптивное управление динамическим объектом на множестве состояний функционирования // Информатика и системы управления. — 2012. — № 4 (34). — С. 107–118.
