Данная статья написана в 20-х числах марта 2020 г. в разгар пандемии короновируса COVID-19, когда ее итоги в России и в других странах еще не были понятны. На примере исследования простой математической модели показаны возможные сценарии распространения пандемии в зависимости от мер государства, направленных на борьбу с ней.
Ключевые слова: единица времени, математическое моделирование, математическая модель, изоклина бесконечности, изоклина нуля, четверть поля, число заражений, константа, модель, число.
Введение
В государстве в единицу времени осуществляется множество случаев вирусного заражения и осуществляется государственная борьба с пандемией путем проведения множества антивирусных актов. Можно рассмотреть не число антивирусных мероприятий, а количество ресурсов (например, денег) выделяемых государством на борьбу с пандемией, при этом как модель, так и вытекающие из нее выводы не меняются.
Обозначения.
С — число новых заражений в единицу времени.
Р — число антивирусных мероприятий, проводимых государством.
Гипотезы.
- Скорость роста числа новых заражений за единицу времени пропорциональна числу уже зараженных и числу антивирусных государственных мероприятий.
В терминах математической модели
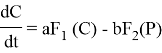
- Скорость увеличения или уменьшения числа антивирусных мероприятий, проводимых государством пропорциональна общей численности зараженных и темпу ее изменения.
В терминах математической модели:
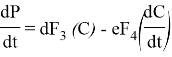
В уравнениях a, b, d, e — положительные константы. F1, F2, F3, F4 — непрерывные функции.
Подробно будем рассматривать случай F1 (С)=С, F2 (Р)=P, F3 (C)=C, 
.
Система обыкновенных дифференциальных уравнений будет иметь вид:
(1) 
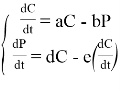
Где a, b, d, e = const≥0.
Систему уравнений (1) удобно исследовать в плоскости переменных Р и С сведя ее к одному уравнению:
(2) 
Уравнение (2) имеет особую точку С=0, Р=0.
(3) Изоклина 0:
(4) Изоклина ∞: 
Утверждение 1. Для первой четверти поля интегральных кривых С, Р изоклина нуля (3) лежит выше изоклины (∞) так как для любых положительных величин 
Заметим, что точки, соответствующие началу снижения числа заражений в единицу времени, лежит на изоклине 0 (3).
Собственные значения системы (1) являются решением уравнения:
(5) 
, где 
Получаем в зависимости от знака D три случая.
1. D<0 
- комплексные числа с вещественной частью отличной от нуля, особая точка С=0, Р=0 — фокус. На рисунке 1 прямая 1-изоклина нуля, 2 — изоклина бесконечности.
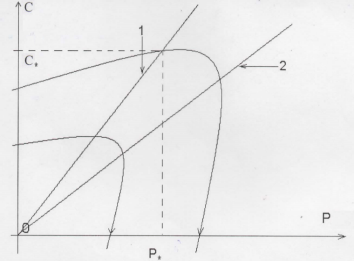
Рис.1.
Наглядный вывод для данного случая: при заданном уровне заражения С государство вырабатывая стратегию борьбы, то есть выбирая Р1 определяется с целью борьбы. Если нужно, добиться, чтобы число заражений перестало расти то минимальное число антивирусных актов нужно выбрать
. C течением времени система приходит к нулевому уровню новых заражений и конечными затратами на борьбу с пандемией.
2. D>0 - различные вещественные, положительные. Особая точка С=0, Р=0 — узел.
В этом случае сепаратриса узла имеет вид:
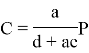
Утверждение 2. В случае a
Картина интегральных кривых имеет вид:
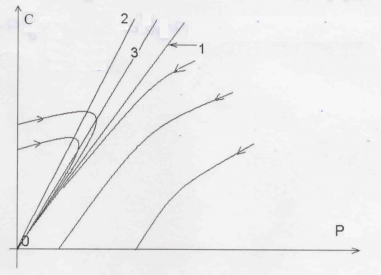
Рис.2. 1 — сепаратриса узла, 2 — изоклина нуля, 3 — изоклина бесконечности
Из рисунка видно, что при любых начальных данных система приходит в точку (0,0). Нулевой уровень новых заражений и нулевые затраты государства. Однако если государство выделяет недостаточно ресурсов на первом этапе, то на число заражений, все-таки сначала будет расти. Это случай инфекций с невысокой скоростью распространения (константа а из системы (1)).
Утверждение 3. В случае a>be сепаратриса узла в первой четверти поля интегральных кривых С, Р (для С, P > 0) лежит выше изоклин 0 (3) и ∞ (4) Картина интегральных кривых имеет вид:
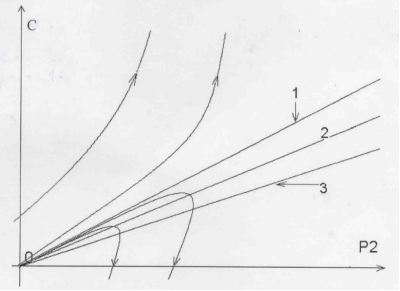
Рис.3.1 — сепаратриса узла, 2 — изоклина нуля, 3 — изоклина бесконечности
Этот случай наиболее реалистичен для нынешней пандемии короновируса COVID-19. Новый, не изученный вирус, с возможностью быстрого распространения (константа а из системы (1)) и недостаточный эффект от мер государства против ее распространения (константа в из системы (1)) и недостаточная реакция на скорость распространения инфекции (константа e из системы (1)). Видно, что изоклины делятся не 2 вида. В первом случае государство изначально недооценив опасность (выделение недостаточных ресурсов на первом этапе) вынуждено постоянно увеличивать свои траты (это можно назвать «догоняющим» сценарием), однако это не позволяет избежать катастрофы (неограниченное увеличение числа новых заражений). Во втором случае, государство выделив достаточно средств (начальная точка будет лежать ниже сепаратрисы узла) приводит к тому что число заражений со временем стремится к нулю. То есть для реализации этого сценария государство должно в первый же момент проводить число антивирусных актов не менее чем 
Отметим, что при a=be значение D из (5) меньше нуля и особая точка — фокус. Мы подробно не рассматриваем этот случай, так как он имеет чисто математический интерес.
3. D=0 =(be-a)/2, особая точка С=0, Р=0 — вырожденный узел. Все утверждения и выводы из предыдущего случая имеют место.
Выводы
Задача государства по борьбе с распространением пандемии короновируса COVID-19 и других вирусных инфекций состоит в выборе стратегии поведения в сложившейся ситуации. Модель наглядно показывает, что для успешного противостояния распространению инфекции от государства требуется не только проведение антивирусных мероприятий (переменная Р в модели (6)) сколько точная оценка реального положения дел: информации об общем числе зараженных (переменная С в модели (6)), об эффективности антивирусных мероприятий (константа b в модели (6)), особенности распространения вируса (константа а из модели(6)). Государство должно выстроить четкую систему реагирования на ситуацию (константы d и e в модели (6))). Все это позволит при затрате минимально необходимых ресурсов выполнить поставленную задачу. Например, ограничить число зараженных какой-то приемлемой величиной или полностью победить пандемию. Из рисунка (3) видно, что, даже имея огромные ресурсы если неверно оценить начальный уровень распространения инфекции не удастся избежать катастрофического сценария. Мы не приводим примеры из разных стран потому что ситуация развивается, и чем одна закончится для каждой конкретной страны, пока не известно. Но тем не менее уже очевидна неэффективность «догоняющего» сценария, когда государство в ответ на увеличение числа зараженных вводит новые меры, но не может прекратить разрастание пандемии.
Заключение
Основываясь на методологии математического моделирования применительно к проблематике распространения вирусной инфекции удается изучить различные сценарии заражения населения в зависимости от действий государства. При исследовании учитывалась зависимость скорости распространения инфекции от общего числа инфицированных в стране, активности государства по борьбе с пандемией. Мы не учитываем число выздоровевших, так как до сих пор точно не известно, приобретают ли они иммунитет, зависимость распространения вируса от природных условий, уровень сознательности населения и т. д. Все уточнения можно ввести в модель, однако, на основных выводах они не отразятся.
Литература:
- Самарский А. А., Михайлов А. П. Математическое моделирование: Идеи. Методы. Примеры.. — ISBN: 5–9221–0120-X. — М.: Физматлит, 2002. — 320 с.
- Михайлов А. П., Шамрай А. А. Численное моделирование некоторых одномерных автомодельных течений идеального газа // Математическое моделирование. — 1998. — № 10:6. — С. 31–41.
- А. П. Михайлов, В. В. Степанова, А. А. Шамрай. Существование и свойства автомодельных решений задачи коши для уравнений газовой динамики // Журнал вычислительной математики и математической физики. — 1996. — № 36:3. — С. 52–65.
