Одной из характерных задач проектирования судов, экранопланов и гидросамолетов является процесс обтекание потоком жидкости со свободной поверхностью тел специфической формы: цилиндр, клин, аэродинамический профиль. Верификация программных комплексов трехмерного численного моделирования является необходимой составляющей внедрения данных программных продуктов в конструкторскую практику. В связи с этим проведенное в данной работе исследование является актуальной задачей.
Известно, что при стремительном течении тяжелой жидкости могут возникать при определенных условиях прыжки, т.е. подъемы уровня жидкости [2].
При гидравлическом скачке возникает обратное течение в верхних слоях воды, движение бурное, поток насыщен пузырьками воздуха.
Подъем жидкости происходит при обтекании тела в потоке, например, крылового профиля или цилиндра.
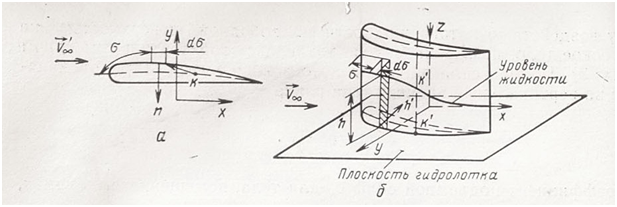
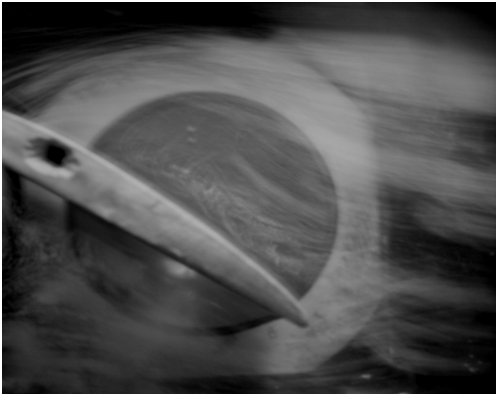
Зная уровни потока жидкости перед обтекаемым телом и за ним можно определить силу сопротивления, а по эпюре распределения давлений – подъемную силу. На рисунке 1 показана схема обтекания крылового профиля потоком.
Рисунок 1 – Схема обтекания крыла в гидролотке
Были выполнены экспериментальные исследования обтекания тел различной формы (цилиндр, крыловой профиль) в гидролотке.
Для визуализации картин течения в гидролотке использован алюминиевый порошок.
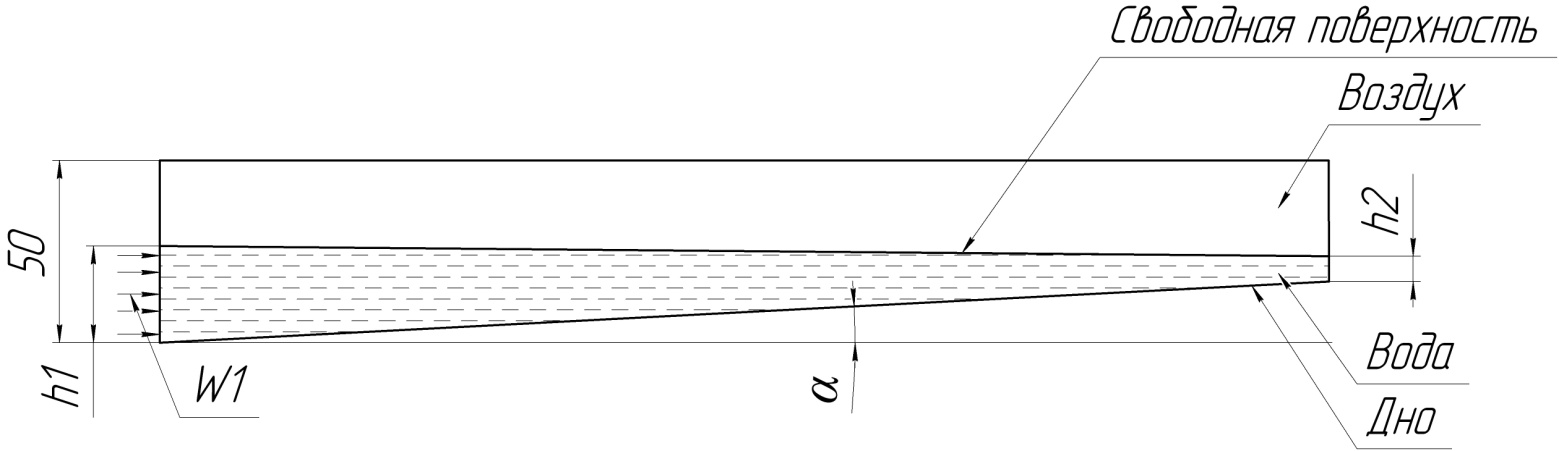
Схема течения в гидролотке показана на рисунке 2. Есть возможность варьировать угол между плоскостью дна гидролотка и горизонтальной поверхностью в пределах -10°, +10°.
Рисунок 2 – Схема течения в гидролотке
- W1 – скорость на входе в рабочую часть лотка; h1, h2 – уровни жидкости на входе и на выходе, соответственно, α – это угол установки дна гидролотка.
Размеры рабочей зоны гидролотка 245х320 мм. Расстояние от входа в рабочую часть лотка до исследуемого тела 80 мм. Диаметр исследуемого цилиндра 45 мм, хорда крылового профиля ClarkY b=120 мм.
Диапазон варьирования скорости на входе, за счет изменения массового расхода воды и угла наклона дна, составляет 0,01-0,3 м/с.
На высоких скоростях при визуализации алюминиевыми опилками были видны только прямые линии тока, опилки уносились основным потоком. Поэтому в исследованиях был выбран угол наклона дна установки 3°.
Исследовались два режима течения: с минимальным массовым расходом воды и с максимальным, при этом скорость на входе в рабочую часть составляла 0,03 и 0,1 м/с, соответственно.
Обтекание крыла исследовалось при углах атаки 0 и 30° со скоростью на входе 0,03 м/с. При анализе обтекания цилиндра использовались 2 режима течения. Таким образом, получено по 4 картины распределения скоростей в гидролотке.
В программном комплексе ANSYS выполнено численное моделирование течений, соответствующие экспериментам в гидролотке.
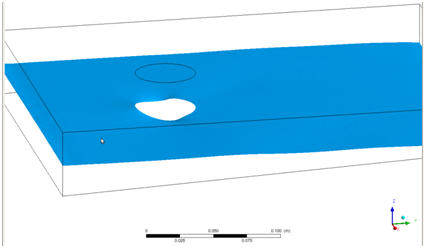
Для построения сеток использован модуль CFX-Mesh в ANSYS Workbench. Данный модуль позволяет создавать преимущественно тетраэдрическую сетку с призматическими слоями вдоль стенок, локальным измельчением в точках, на линиях и поверхностях. Построены две сеточных модели для крыла с углом атаки 0 и 30° и одна модель для обтекания цилиндра. Максимальный размер объемной ячейки 6 мм; размер поверхностных ячеек 3…6 мм.
Для моделей с крылом суммарное число ячеек составило 2,7-2,8 млн. Для модели обтекания цилиндра количество ячеек составило 1,88 млн. (рис. 3).
Граничные условия для крыла и цилиндра аналогичные.
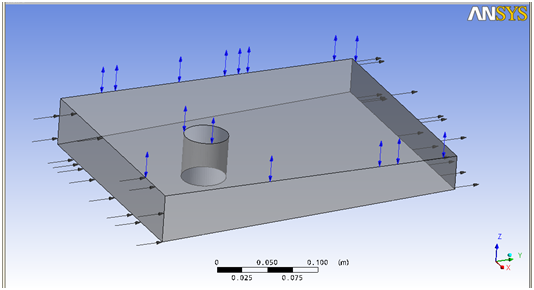
Поскольку эксперимент ставился для двух условий – со скоростью 0,03 и 0,1 м/с на входе, созданы две комбинации граничных условий. Постановка задачи в CFX-Pre рассмотрена на примере цилиндра (рисунок 4).
Рисунок 3 – Сеточные модели обтекания профиля и цилиндра
1 2
Рисунок 4 – Расчетная область с расставленными граничными условиями
1 – Вход (Inlet); 2 – Стенка (Wall); 3 – Открытая поверхность (Opening); 4 - Поверхность цилиндра; 5 – Выход (Outlet)
Картина обтекания цилиндра без отрыва показана на рисунке 5. Как видно из картины обтекания, полученной в эксперименте на рисунке 5 а, течение ламинарное. Такое же распределение скоростей и отсутствие отрыва потока наблюдается в картине распределения скоростей, полученной моделированием, на рисунке 5 б. Состояние жидкости показано на рис. 6
Режим течения со скоростью на входе 0,03 м/с. Число Re равно 1350. Полученный результат свидетельствует об адекватном задании граничных условий и общих параметров в CFX-Pre, такая постановка задачи может быть использована при моделировании более сложных задач течения в гидролотке.
а б
Рисунок 5 – Картины безотрывного обтекания цилиндра
Если сравнивать полученное ламинарное течение с ползущим [1], то видно, что в ламинарном режиме область возмущения за цилиндром более вытянутая.
Рисунок 6 – Свободная поверхность, ризб=0 Па
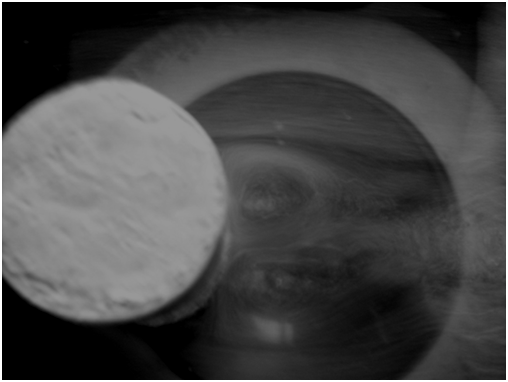
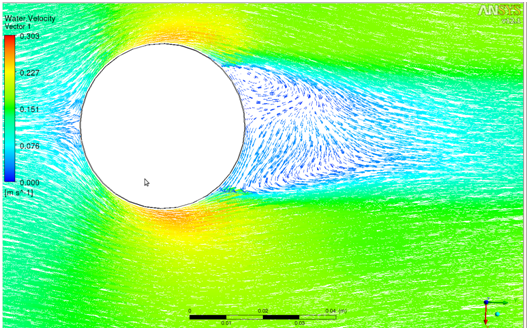
При скорости на входе в рабочую часть лотка W = 0,1 м/с, получен отрыв потока (рисунок 7 а). Фотография получена с выдержкой 1 с. За цилиндром видны два вихря. В ANSYS CFX при соответствующих условиях получен отрыв потока за цилиндром, при число Re равном 4500.
а б
Рисунок 7 – Отрыв потока жидкости от цилиндра
Похожая картина обтекания цилиндра приведена в альбоме течений жидкости и газа [1]. Таким образом, можно заключить, что течение в ANSYS CFX смоделировано правильно.
По распределению давлений на поверхности цилиндра можно определить силу, действующую на него.
При скорости 0,03 м/с число Re, рассчитанное по хорде крыла, составило 3600. Для нулевого угла атаки течение безотрывное (рисунок 8). Полученная картина течения согласуется с приведенными в [1].
Рисунок 8 – Безотрывное обтекание крыла при угле атаки 0°, полученное в эксперименте и моделированием в ANSYS CFX
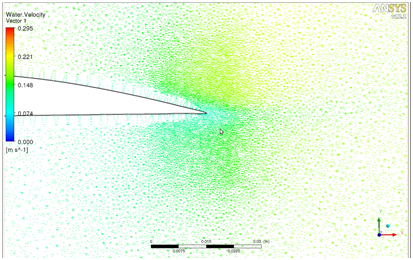
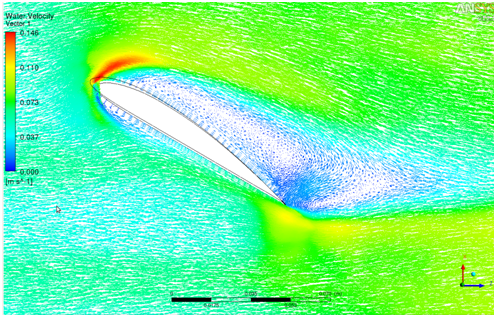
При числе Re=3600, но уже с углом атаки профиля 30° возникает отрыв потока по всей спинке крыла, как в натурном эксперименте (рисунок 9), так и в ANSYS CFX (рисунок 10). При турбулентном течении жидкости отрыв потока происходит не по всей спинке, а ближе к задней кромке, т.к. при более интенсивной турбулентности происходит перемешивание ламинарного и турбулентного потока [1].
Рисунок 9 – Экспериментальное обтекание профиля с большим углом атаки
Рисунок 10– Отрыв потока при угле атаки 30°
Проведенное моделирование показало, что происходит подъем уровня жидкости на входной кромке крыла и уменьшение уровня жидкости к выходной кромке, такая же картина наблюдалась и в эксперименте.
- Заключение
Результаты моделирования течений, полученные в натурном и численном эксперименте, показали хорошее совпадение между собой и с картинами течения полученными в эталонных экспериментах [1], что говорит о корректной постановке эксперимента в гидролотке.
Результаты, полученные в ANSYS CFX, свидетельствуют об адекватном моделировании, а именно: правильном построении сетки, заданиb граничных и начальных условий, заданиb общих параметров течения.
Проведенные исследования показали возможность моделирования более сложные течения, например, при определении характеристик обтекания судов, корпусов летательных аппаратов и различных гидротехнических сооружений.
Работы выполнена при финансовой поддержке Министерства образования и науки РФ.
Литература:
1. Альбом течений жидкости и газа: Пер. с англ./Сост. М. Ван-Дайк. – М.: Мир, 1986. – 184 с., ил.
2. Виноградов Р.И. и др. Газогидравлическая аналогия и ее практическое приложение / Р. И. Виноградов, М.И. Жуковский, И.Р. Якубов. – М.: Машиностроение, 1978. – 152 с., ил.