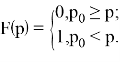При реализации проектов всегда присутствуют сведения, нарушение целостности или неправомочный доступ к которым могут привести к неблагоприятным последствиям, таким, например, как срыв проекта, судебный процесс, санкции со стороны заказчика и т. д. Все это является угрозами для реализации благополучного завершения проекта. Определяются угрозы вероятностью реализации.
Так как вероятность реализации угрозы (как и другие её количественные характеристики) есть величина неопределённая (либо заданная с некоторой погрешностью), можно с помощью теории нечётких множеств и субъективной вероятности (экспертная оценка) формализовать неоднозначность исходных данных. Для определения наиболее весомых (или напротив незначительных) угроз для модели безопасности, либо выявления факта, что однозначное указание вероятности реализации той или иной угрозы не скажется на выполнении проекта, необходимо получить распределение непрерывной случайной величины (далее НСВ) [1].
Ключевые слова: модель, безопасность, угроза, уязвимость, распределение НСВ.
In the course of the activities of various organizations, projects are carried out. When implementing projects, there is always information, violation of integrity or unauthorized access to which can lead to adverse consequences, such as disruption of the project, litigation, sanctions by the customer, etc. All this is a threat to the successful completion of the project. Threats are determined by the likelihood of implementation.
Since the probability of a threat (like its other quantitative characteristics) is an uncertain value (or given with some error) using the theory of fuzzy sets and subjective probability (expert judgment), we can formalize the ambiguity of the source data. To determine the most significant (or, on the contrary, insignificant) threats to the security model, or to identify the fact that an unambiguous indication of the likelihood of a particular threat will not affect the implementation of the project, it is necessary to obtain a distribution of a continuous random variable (hereinafter referred to as NSV [1]).
Основной целью данной работы является получение распределения реализации угроз, анализ модели угроз и уязвимостей безопасности проекта для выявления наиболее существенных, часто реализуемых и требующих устранения угроз.
Для достижения поставленной цели необходимо разработать алгоритм получения распределения вероятности реализации угрозы либо цепочки угроз [2].
Любое измерение, как и оценка, не являются абсолютно точными.
В количественных измерениях указывают вероятную ошибку измерения или интервал, в котором с данной вероятностью находится измеренная величина.
Базовым понятием в теории мягких измерений величин является шкала. Но, в отличие от традиционной (количественной) теории измерений, эта шкала может быть, как числовой, так и лингвистической. Оценка величины — это утверждение о степени выраженности некоторого измеряемого свойства объекта, полученное по определенным правилам. Оценивание — процесс получения оценок.
Оценка может быть жесткой или мягкой. Жесткая оценка определяет значение переменной. Мягкая оценка задается распределением вероятности переменной, степенью соответствия переменной некоторому понятию или функцией принадлежности.
Применение теории нечетких множеств и субъективной вероятности позволяет формализовать неоднозначность и неопределенность используемых данных.
Модель полной определенности («жесткая оценка»)
В данной модели вероятность ![]() является вещественным числом, которое может принимать значения в диапазоне от 0 до 1:
является вещественным числом, которое может принимать значения в диапазоне от 0 до 1:
![]()
Распределение СВ в данной модели — вырожденное.
Функция распределения имеет вид ступеньки:
|
|
График функции распределения F(p):
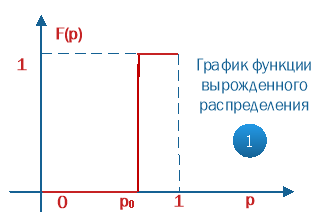
Рис. 1. График функции распределения в вырожденном случае
Плотность распределения этой случайной величины имеет вид дельта-функции:
![]()
График плотности вырожденного распределения:
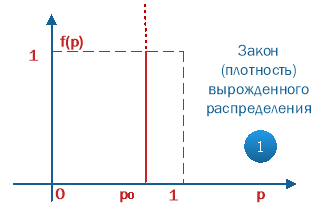
Рис. 2. Плотность вырожденного распределения
Модель ошибки (мягкая оценка)
В данной модели вероятность ![]() является вещественным числом, которое может принимать значения в диапазоне от 0 до 1, причем вероятность задается с некоторой погрешностью Δp:
является вещественным числом, которое может принимать значения в диапазоне от 0 до 1, причем вероятность задается с некоторой погрешностью Δp:
![]()
![]()
![]()
Вероятность угрозы в данной модели рассматривается как непрерывная случайная величина ξ с некоторым распределением:
![]() (1)
(1)
где ![]() вероятность реализации данного значения ξ.
вероятность реализации данного значения ξ.
В теории погрешностей это распределение полагается равномерным.
Функция распределения в этой модели имеет вид:
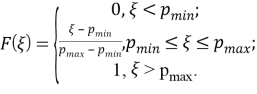
График этой функции имеет вид:
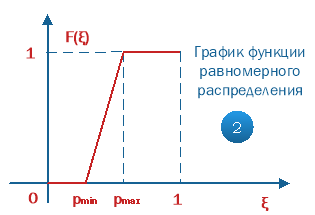
Рис. 3. График функции равномерного распределения
Плотность распределения в этой модели имеет вид:
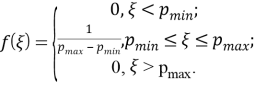
График плотности равномерного распределения представлен на рисунке 4:
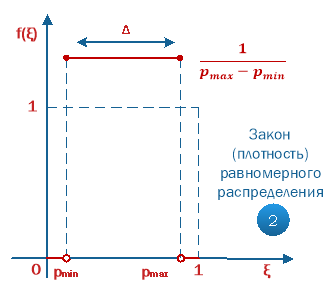
Рис. 4. Плотность равномерного распределения
Характеристики этого распределения [2–3]:
– математическое ожидание;
– дисперсия;
– СКО.
Математическое ожидание вычисляется по формуле:
![]()
Дисперсия вычисляется по формуле:
![]()
СКО вычисляется по формуле:
![]()
Модель с треугольным распределением вероятности угрозы
Поскольку нельзя задать абсолютно точное значение вероятности реализации события (как в модели полной определенности), а равномерное распределение вероятности угрозы не очень реалистично отражает представления о вероятности угрозы (слишком широкий разброс значений), рассмотрим распределение Симпсона (треугольное распределение).
Тогда мода вероятности реализации угрозы равна среднему значению границ диапазона
![]()
Обычные представления о вероятности угрозы предполагают некую «сосредоточенность» вероятности угрозы около некоторого значения. В качестве такового у эксперта запрашивается «наиболее вероятное» значение (т. е., мода распределения). Поэтому распределение (1) моделируют «колоколообразным», сосредоточенным около моды.
Из-за указанных ранее проблем с получением точных значений необходимых величин искать «точный» вид плотности распределения (1) не имеет смысла.
Наиболее простым представляется моделирование (1) в виде несимметричного треугольного распределения [4].
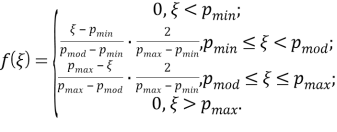 (2)
(2)
График плотности треугольного распределения представлен на рисунке 5:
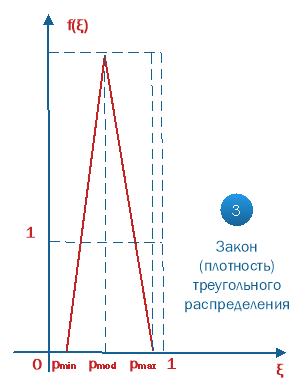
Рис. 5. Плотность несимметричного треугольного распределения
Положение моды распределения, задаваемой параметром ![]() , удобнее задавать с помощью параметра , задающего положение моды относительно границ распределения:
, удобнее задавать с помощью параметра , задающего положение моды относительно границ распределения:
![]()
![]()
Интегрирование (2) дает:
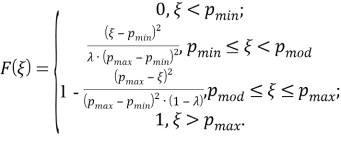
Причем:
![]()
График функции треугольного распределения имеет вид:
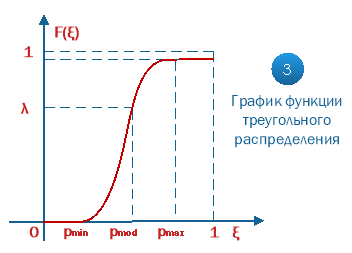
Рис. 6. Интегральная функция треугольного распределения
Характеристики НСВ с треугольным распределением [2–4]:
– математическое ожидание;
– дисперсия;
– СКО.
Математическое ожидание вычисляется по формуле:
![]()
Дисперсия вычисляется по формуле:
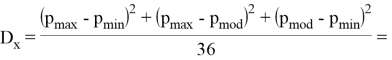
![]()
СКО вычисляется по формуле:
![]()
Метод обратной функции распределения
В теории вероятностей доказывается, что случайная величина
![]() (3)
(3)
имеет равномерное распределение на интервале [0; 1]. Отсюда значение СВ х, имеющей плотность распределения f(x), находится из соотношения
![]() (4)
(4)
Где ![]() — обратная функция распределения этой СВ.
— обратная функция распределения этой СВ.
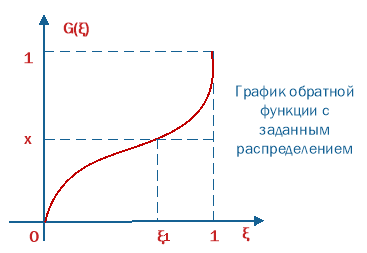
Рис. 7. Идея генерирования НСВ с заданным законом распределения
Основные недостатки метода в том, что аналитически не всегда:
– интеграл (3) берется,
– уравнение (4) решается.
Поэтому для статистического моделирования надо выбирать такие модели распределения вероятности реализации угроз, которые позволяют получить результат без излишних вычислительных затрат.
Обратные функции моделей распределения вероятностей угрозы
Для вырожденного распределения обратная функция распределения постоянна:
![]()
Поэтому при статистическом моделировании вероятности события по этой модели нужно получить только одно БСЧ ξ.
График обратной функции распределения для модели с «жесткой» оценкой имеет вид:
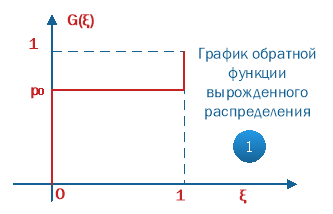
Рис. 8. Обратная функция распределения для «Модели полной определенности»
Для модели на основе погрешностей обратная функция распределения линейна:
![]()
Её график имеет вид:
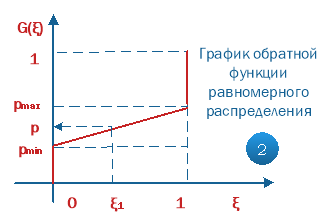
Рис. 9. Обратная функция распределения для модели погрешностей
Для модели с треугольным распределением функция ![]() является кусочной:
является кусочной:
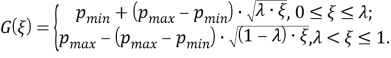
Её график имеет вид:
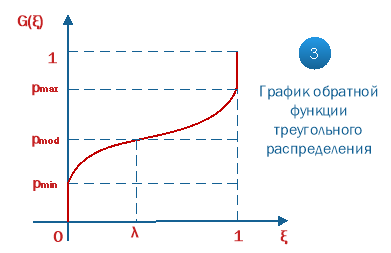
Рис. 10. Обратная функция распределения для модели с треугольным распределением
В данной статье был разработан алгоритм получения распределения вероятности реализации угрозы для различных структур модели угроз. Согласно разработанному алгоритму можно определить наиболее часто реализуемую угрозу (для определенной структуры системы) и предпринять меры по ее устранению. Для исследования распределения НСВ и СВ необходимо провести серию экспериментов с одними и теми же вероятностями событий реализации угроз, фиксируя результаты каждого прогона как отдельное данное. Чем больше таких экспериментов будет проведено, тем более близким к теоретическому получается экспериментальное распределение. Для приблизительной оценки достаточно провести 20 или 30 итераций, для более точных необходимо от 100 до 1000, т. к. проведение большего числа итераций не будет давать значительно лучших показателей погрешности экспериментального значения относительно теоретического и неоправданно увеличит время и используемый объем ресурсов вычислительной машины.
Литература:
- Бутрина Л. П. Применение математического аппарата теории графов при построении модели угроз безопасности // Молодой ученый. — 2019. — № 46. — С. 1–5. — URL https://moluch.ru/archive/284/63983/ (дата обращения: 10.01.2020).
- Гмурман В. Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. — 9. — М.: Высшая Школа Экономики, 2003. — 479с.
- Карлин С. Основы теории случайных процессов. — М.: Мир, 1971. — 536с.
- Треугольное распределение // MATEMATICUS. URL: https://www.matematicus.ru/zakony-raspredeleniya-sluchajnoj-velichiny/treugolnoe-raspredelenie (дата обращения: 19.10.2019).