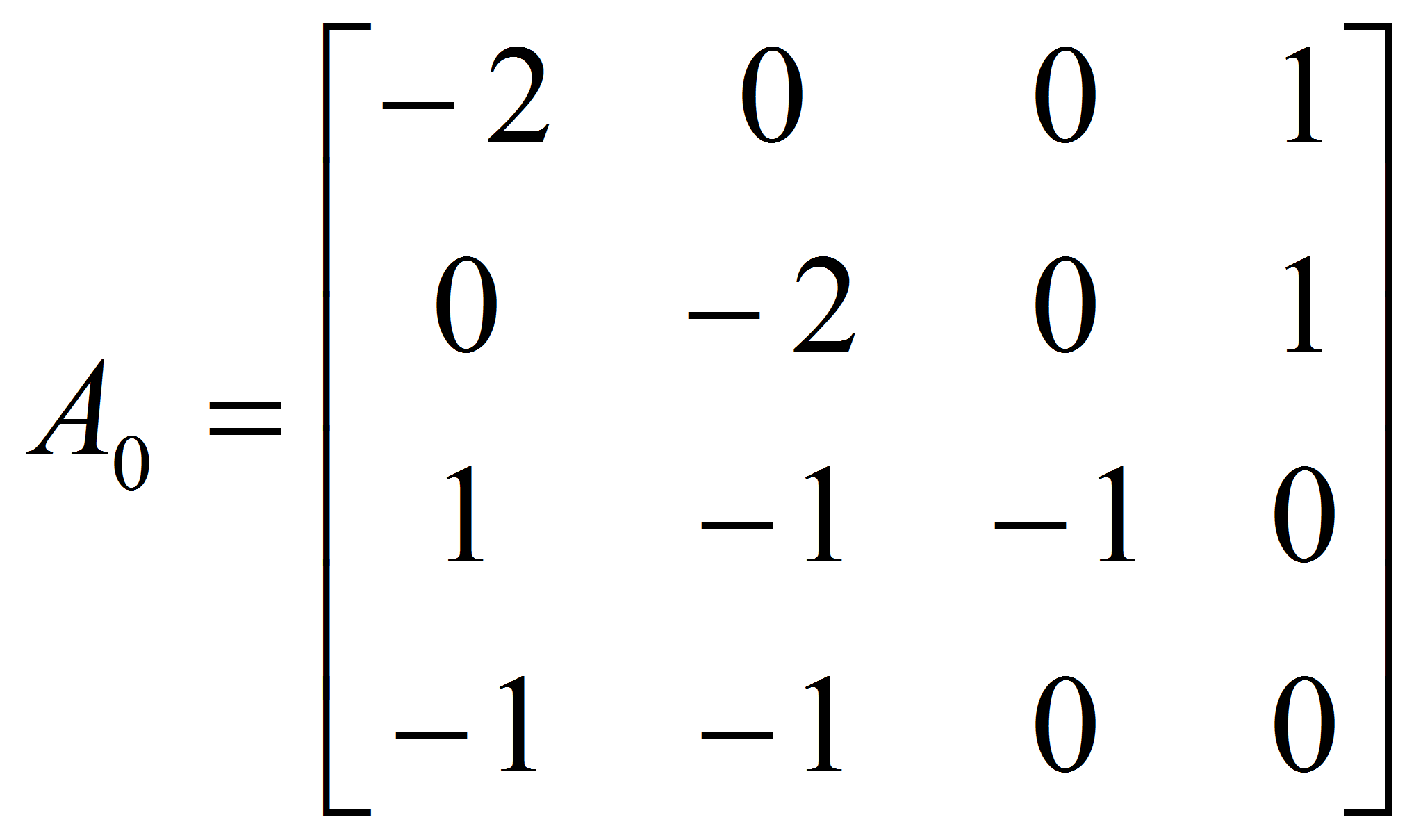1. Введение
-
Построение системы, обеспечивающей требуемое качество
при воздействии на объект внешних возмущений, является одной из
основных проблем современной теории управления. В классе задач
робастного управления существует большое число методов и подходов к
решению данной задачи. Наиболее полно робастная теория и
библиография по ней представлена в [1]. Алгоритм управления,
построенный с использованием внутренней модели гармонических
колебаний, получен в [2-5]. Но одной из основных проблем при синтезе
систем управления, позволяющих компенсировать возмущения, является
задача формирования сигнала, несущего информацию о них, и
позволяющего использовать его для получения нужных оценок. И эта
проблема решена в [6-9], где используется метод вспомогательного
контура, который позволяет выделить сигнал, несущий информацию о
помехах, получить требуемые оценки и скомпенсировать нежелательное
воздействие помех на регулируемые параметры.
- В данной работе предложен способ построения системы управления для линейного объекта, у которого все параметры известны, а на входе и на регулируемом выходе действуют возмущения, причем возмущения эти различны, причем для этого не требуется никаких априорных знаний о параметрах внешних возмущениях. Спроектированная система управления позволяет скомпенсировать влияние помех на регулируемые переменные с заданной точностью и сделать их независимыми от не измеряемых неограниченных возмущений на входе системы. Основные результаты получены с использованием технологии конструктивного вложения систем [10] и метода вспомогательного контура [6-9].
Постановка задачи
Объект управления задан в виде уравнений (1) – (3):
- где
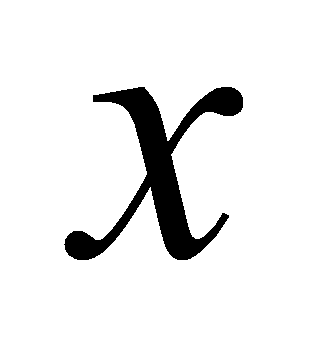 ,
,
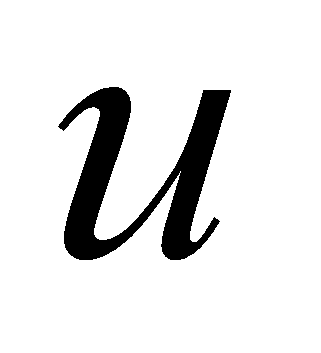 ,
,
 ,
,
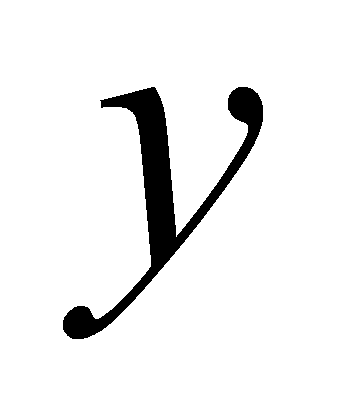 – векторы состояния, управления, измеряемых и регулируемых
параметров соответственно,
– векторы состояния, управления, измеряемых и регулируемых
параметров соответственно,
 – вектор внешних возмущений,
– вектор внешних возмущений,
 – шум на выходе статического звена модели системы;
– шум на выходе статического звена модели системы;
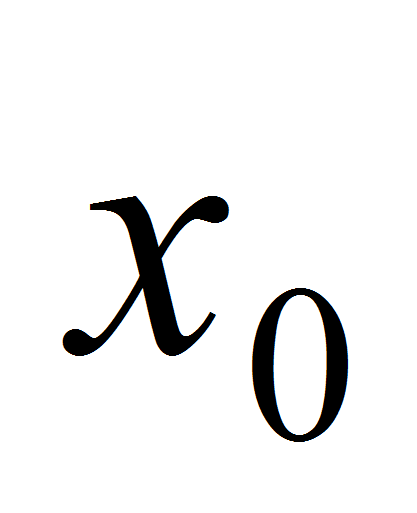 – начальные условия;
– начальные условия; –
числовые матрицы соответствующих порядков.
–
числовые матрицы соответствующих порядков.
- Требуется получить алгоритм функционирования системы управления, которая обеспечивает выполнение целевого условия
- (4)
 при
при
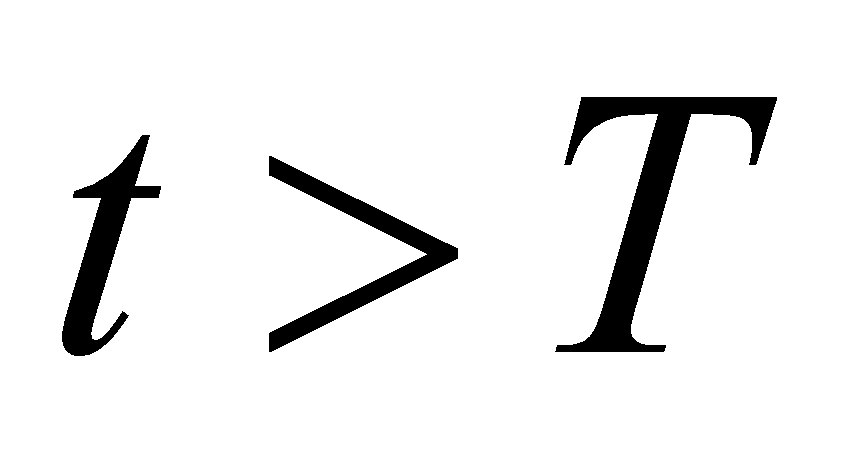 ,
,- где
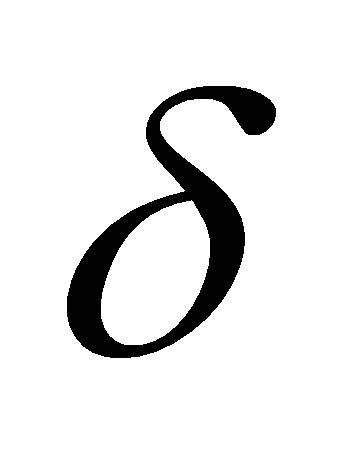 – достаточно малая величина,
– достаточно малая величина,
 – время, по истечении которого должна обеспечиваться требуемая
динамическая точность после включения системы в работу.
– время, по истечении которого должна обеспечиваться требуемая
динамическая точность после включения системы в работу.Предположения:
iii) помеха на выходе системы
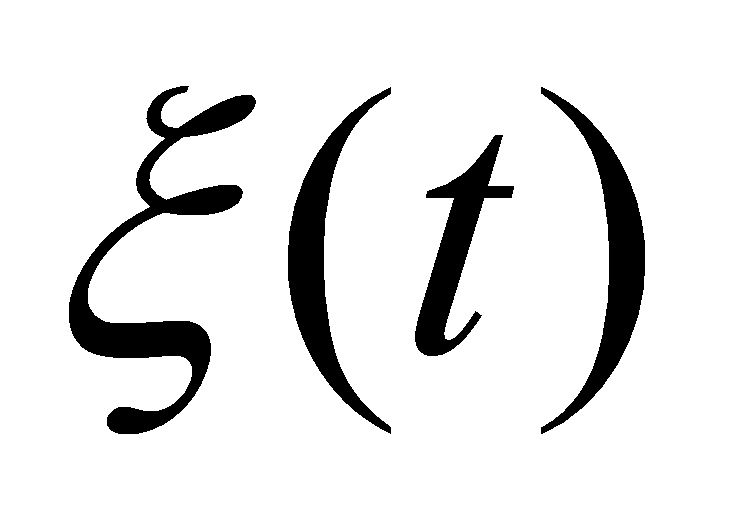 – ограниченная функция;
– ограниченная функция;iv) все матрицы в (1) – (3) известны.
Другие ограничения будут приведены в условиях утверждения.
Метод решения
Будем формировать вектор управления в виде
- где
 – вспомогательное управление измерением;
– вспомогательное управление измерением;
 – числовая матрица регулятора.
– числовая матрица регулятора.
Предварительные сведения о канонизации матриц
- Если матрица неполная (необратимая),
она содержит линейно зависимые строки и/или столбцы. Для описания
линейной зависимости и независимости строк и столбцов матрицы удобно
использовать понятия делителей нуля максимального ранга и
канонизаторов. В [10] канонизацией названо не обязательно
единственное разложение любой матрицы
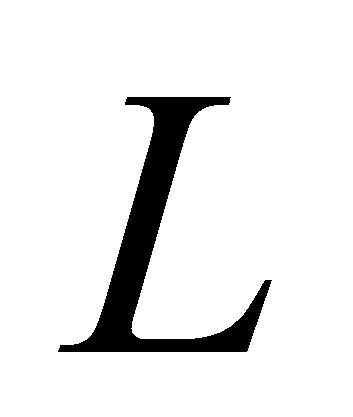 размера
размера
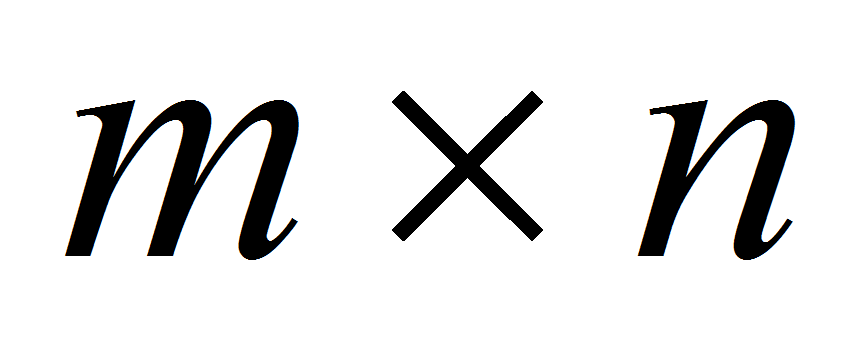 и ранга
и ранга
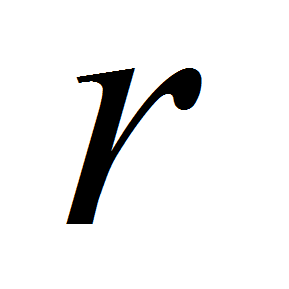 на четверку матриц, удовлетворяющих следующему равенству в блочной
записи
на четверку матриц, удовлетворяющих следующему равенству в блочной
записи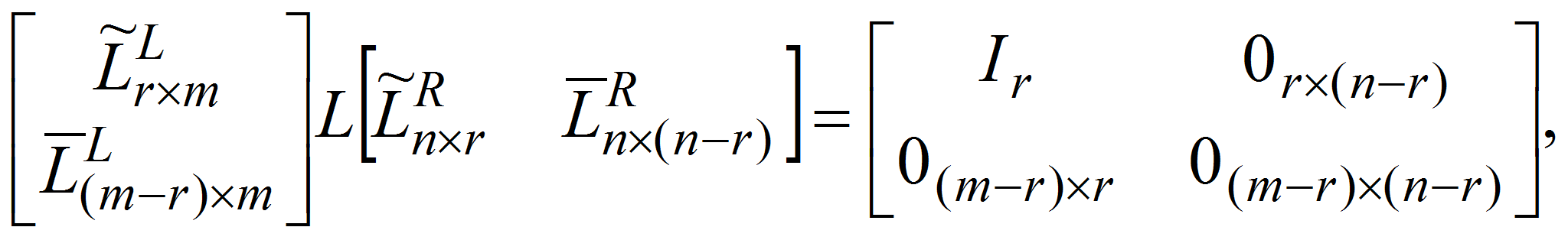
- где
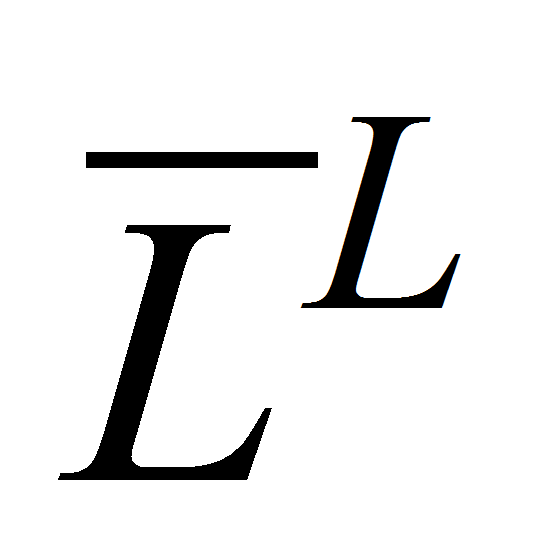 и
и
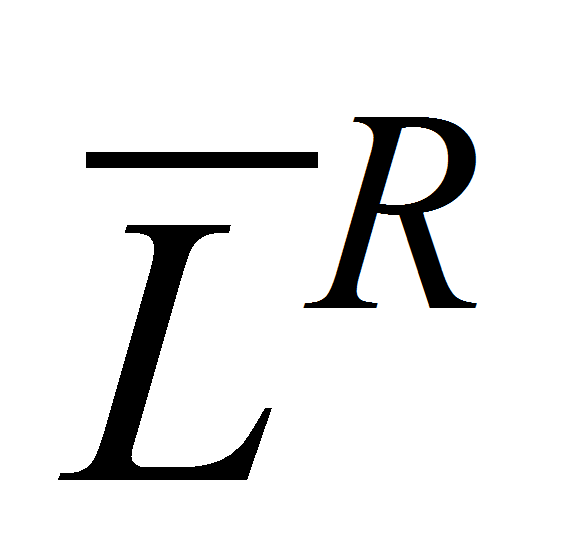 – левый и правый делители нуля максимального ранга,
– левый и правый делители нуля максимального ранга,
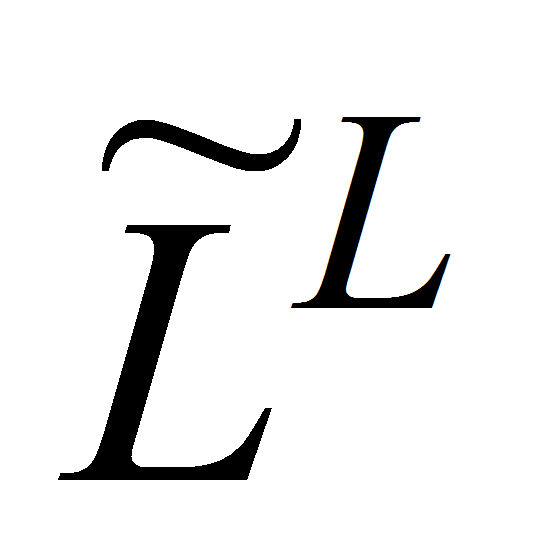 и
и
 – левый и правый канонизаторы (
– левый и правый канонизаторы (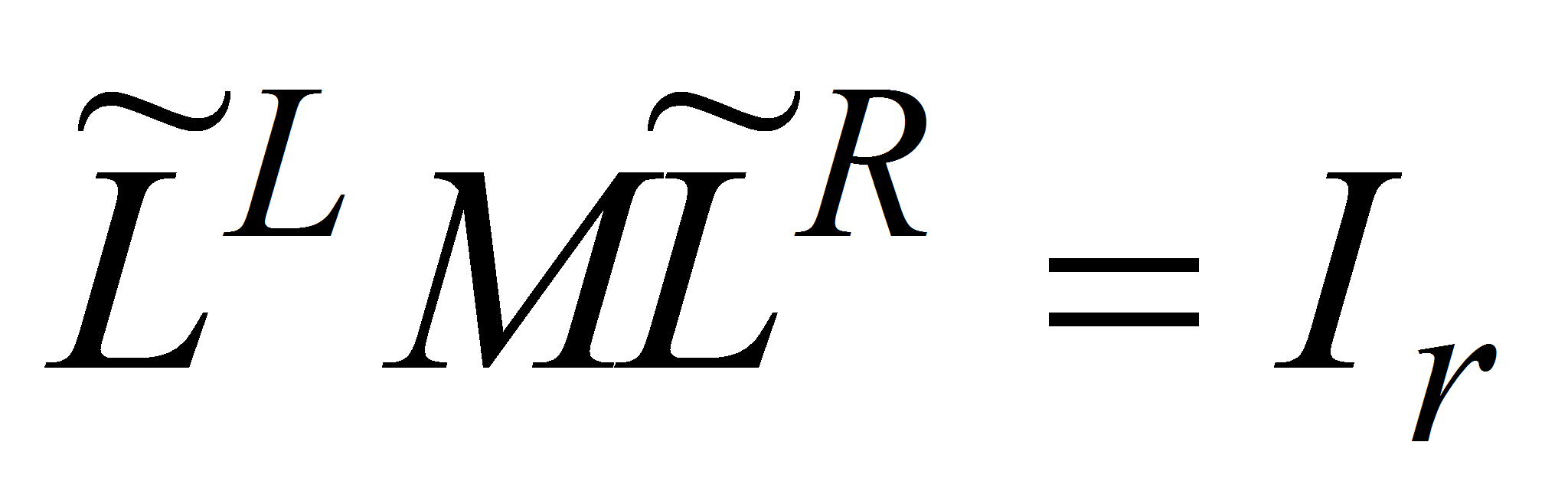 ,
,
 – единичная матрица размера
– единичная матрица размера
 ).
Для любой матрицы
).
Для любой матрицы
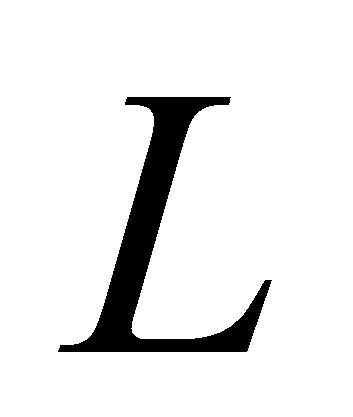 левый
левый
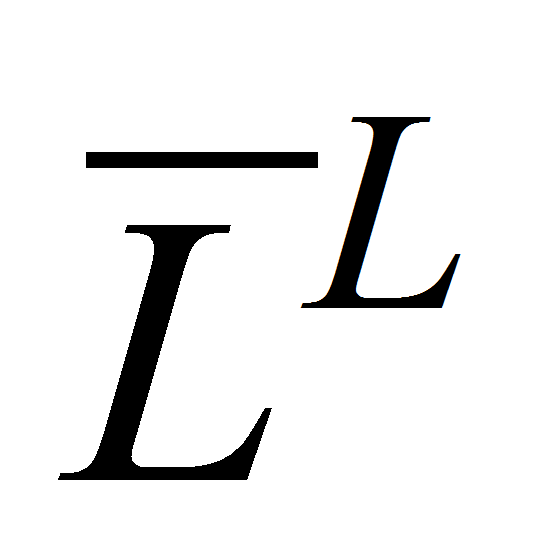 (правый
(правый
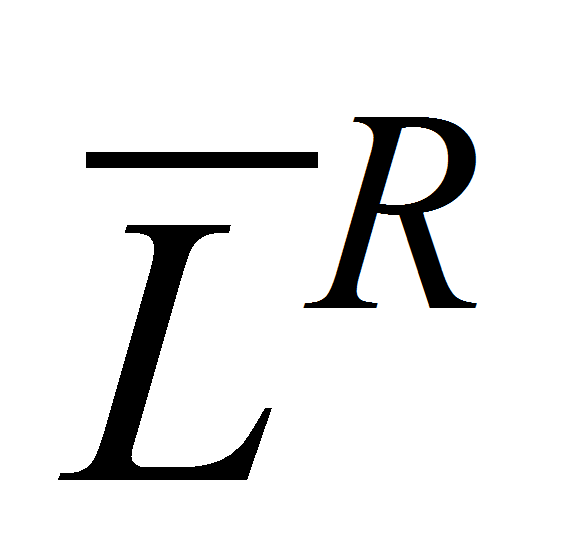 )
делитель нуля максимального ранга характеризует все линейно
зависимые комбинации строк (столбцов) исходной матрицы
)
делитель нуля максимального ранга характеризует все линейно
зависимые комбинации строк (столбцов) исходной матрицы
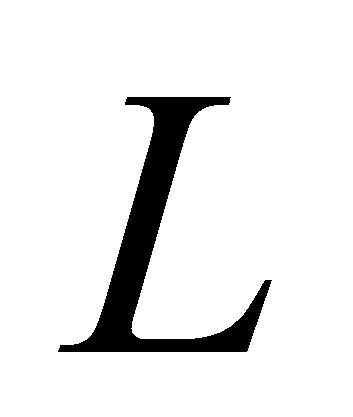 в соответствии с тождеством
в соответствии с тождеством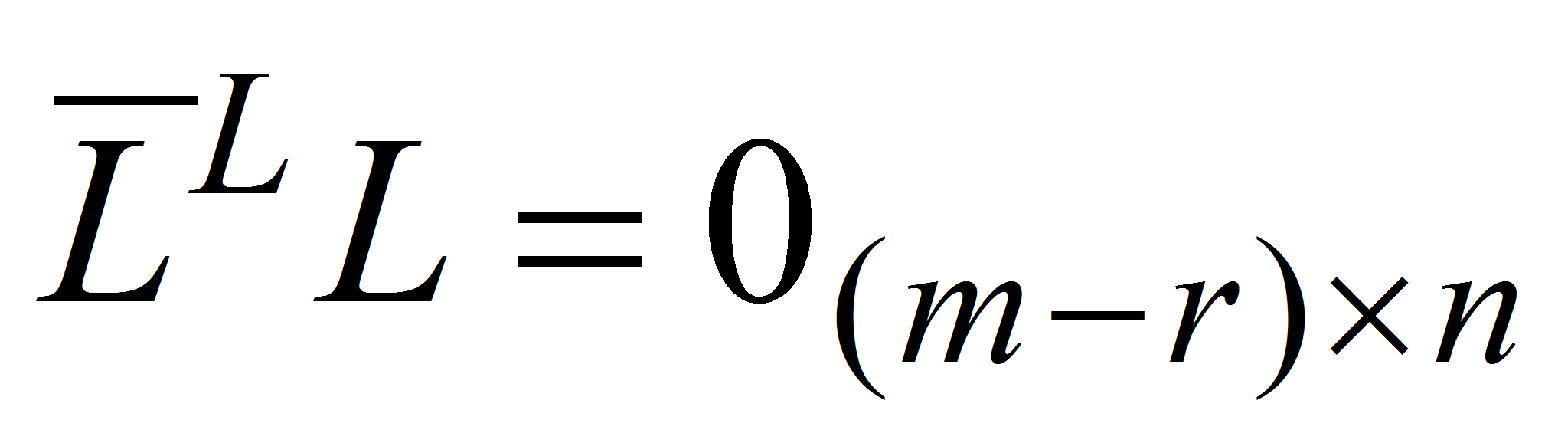 (
( ).
).- При решении матричных уравнений методом канонизации используется понятие сводного канонизатора
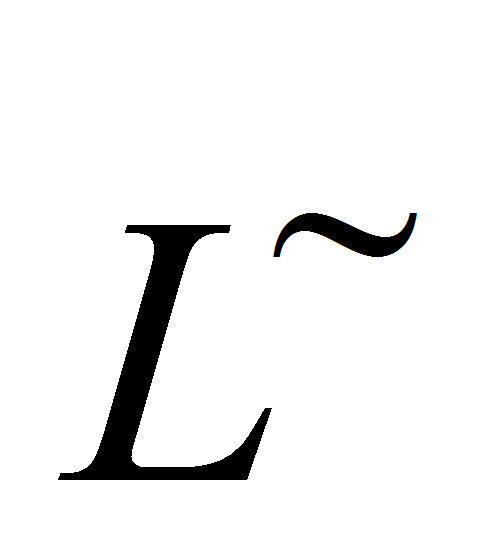 ,
вычисляемого по формуле
,
вычисляемого по формуле
- и удовлетворяющего условиям регулярности по Нейману
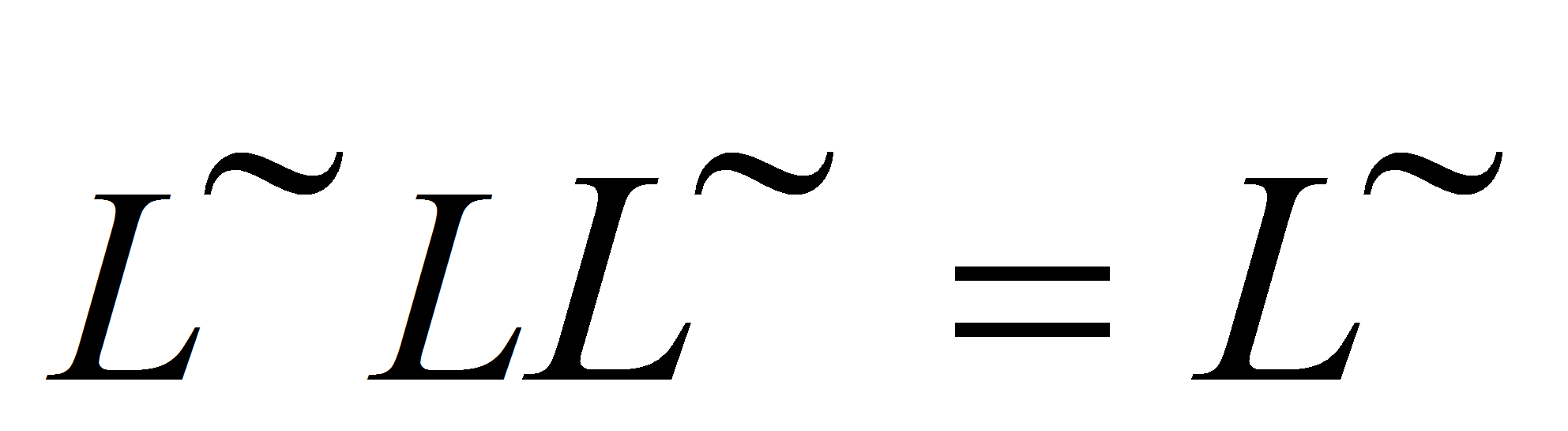 ,
,
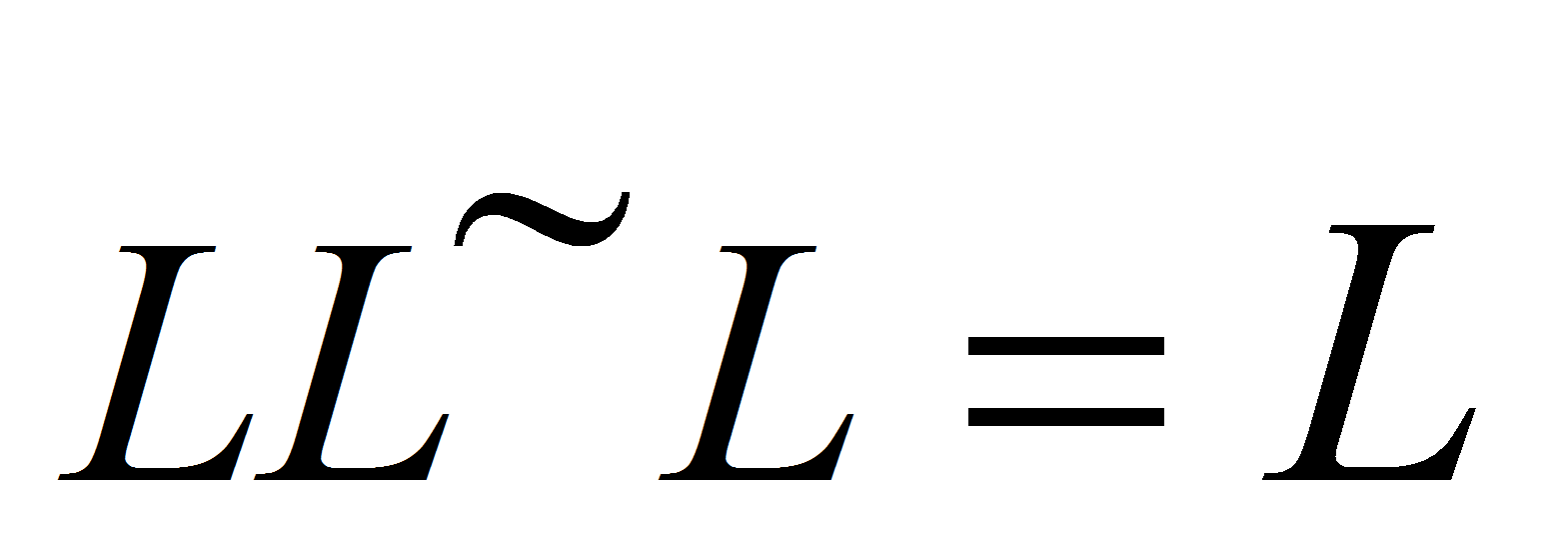 .
.- Сводный канонизатор характеризует совокупность линейно независимых комбинаций строк и столбцов исходной матрицы. Частным случаем сводного канонизатора является псевдообратная матрица по Муру – Пенроузу
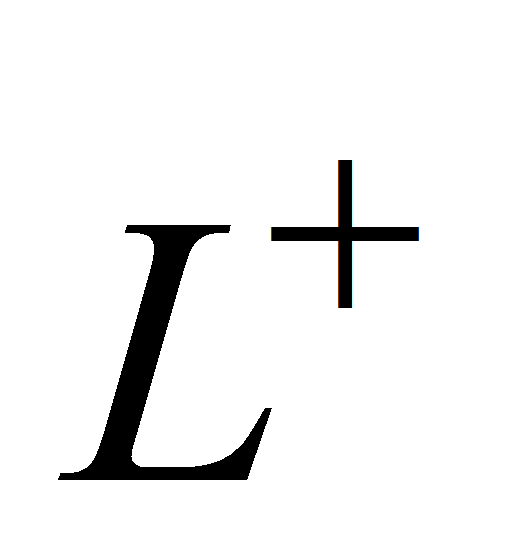 .
Для матрицы полного строчечного ранга сводный канонизатор совпадает
с правым делителем единицы
.
Для матрицы полного строчечного ранга сводный канонизатор совпадает
с правым делителем единицы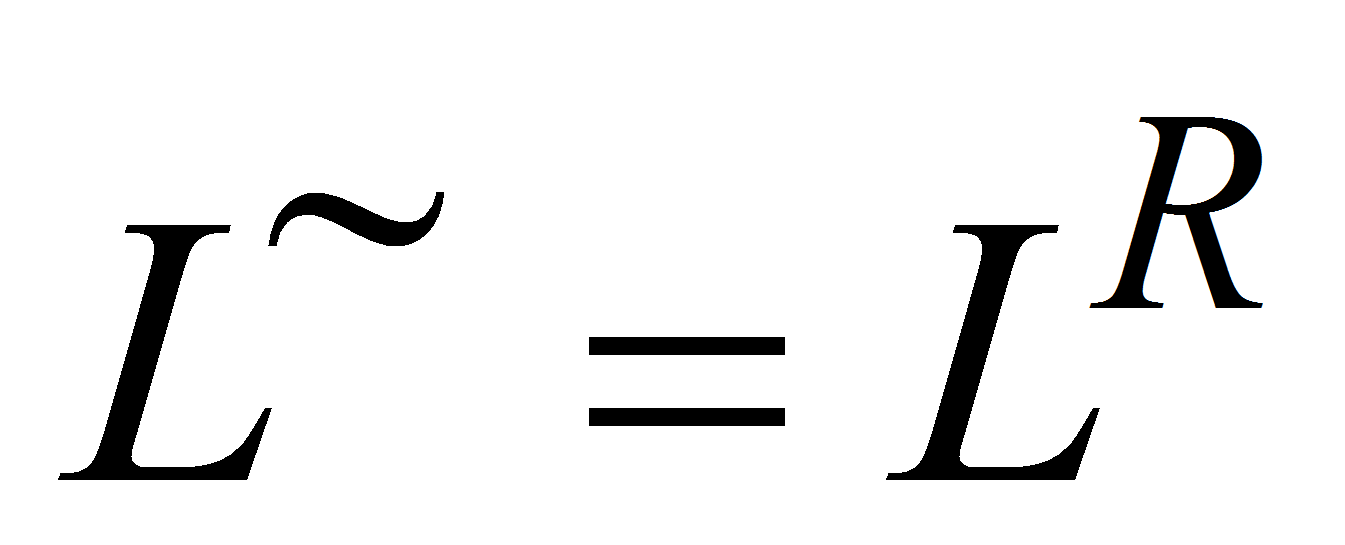 ,
,- а для матрицы полного столбцового ранга – с левым делителем единицы
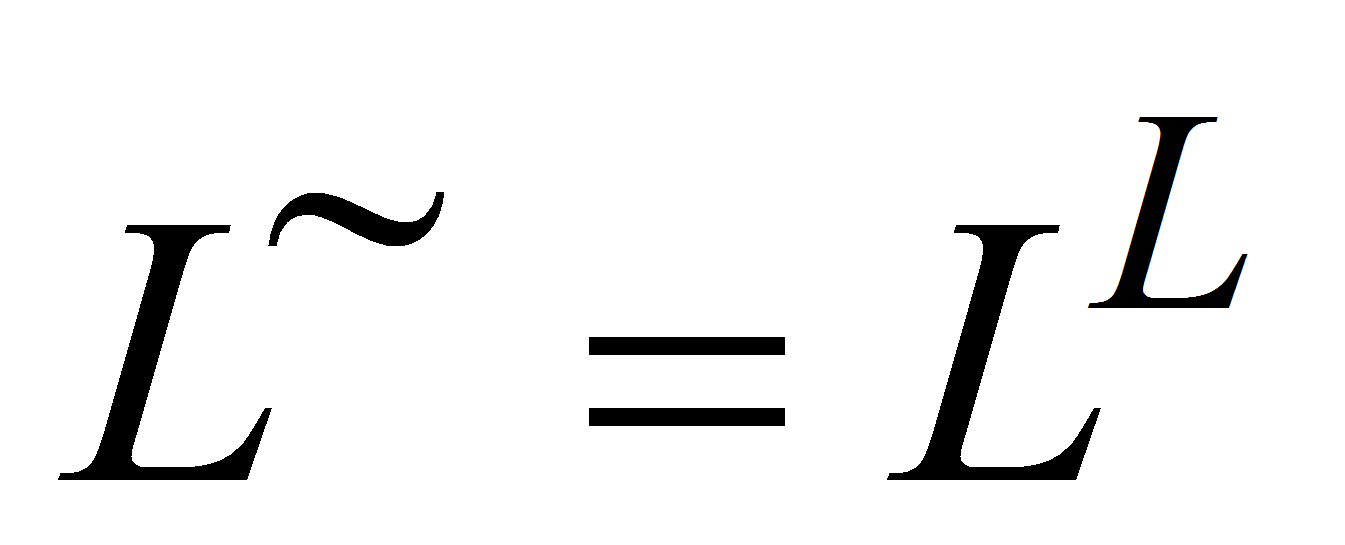 .
.- Правым (левым) делителем единицы для матрицы
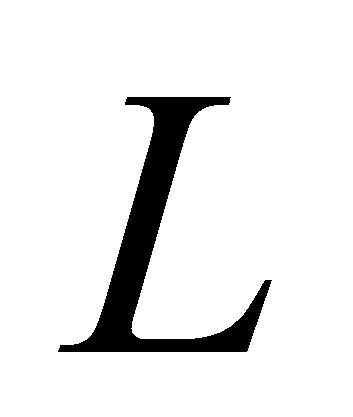 размера
размера
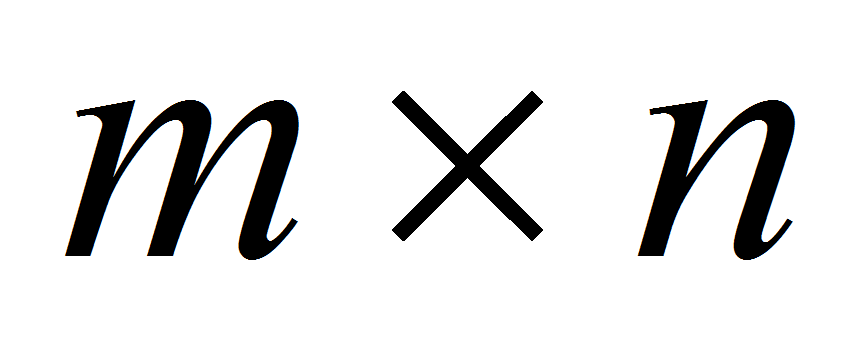 полного строчечного (столбцового) ранга называется матрица
полного строчечного (столбцового) ранга называется матрица
 (
( ),
удовлетворяющая условию
),
удовлетворяющая условию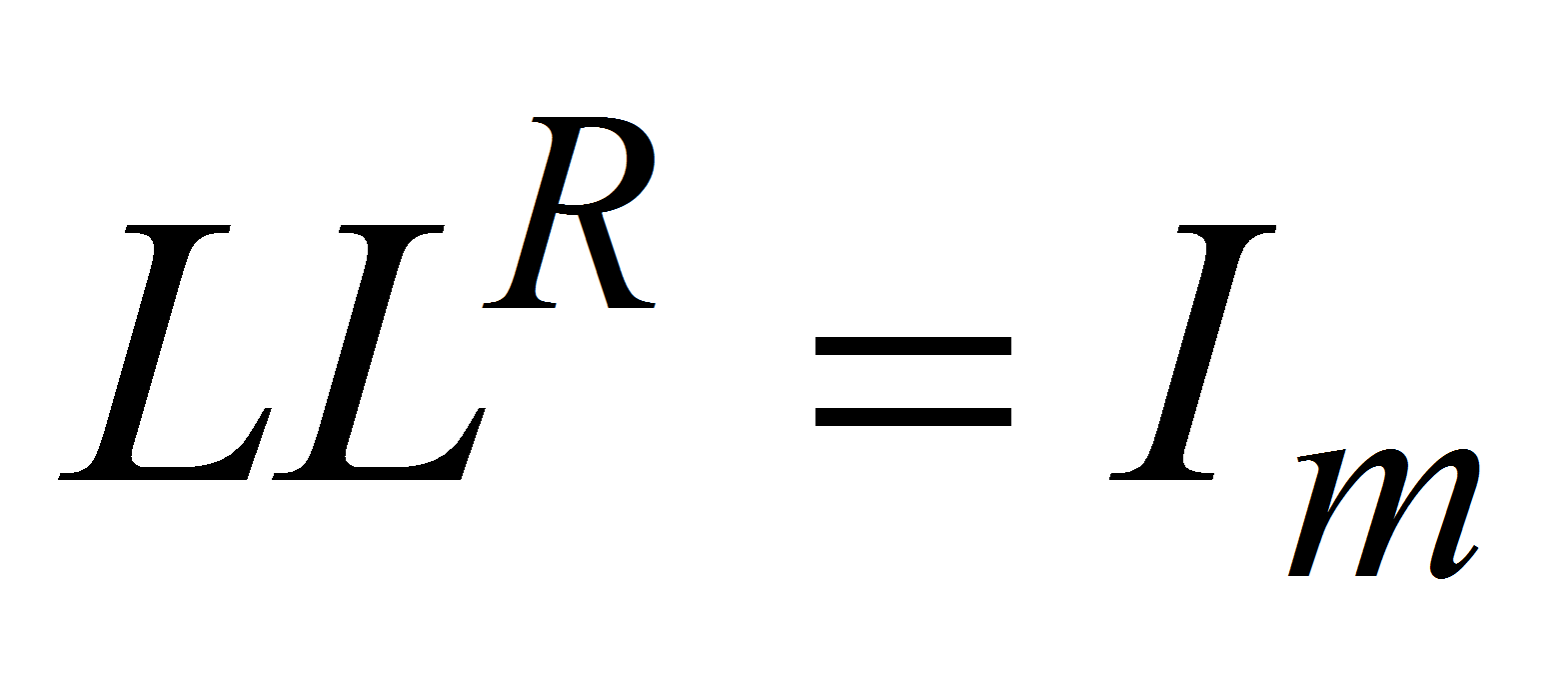 (
(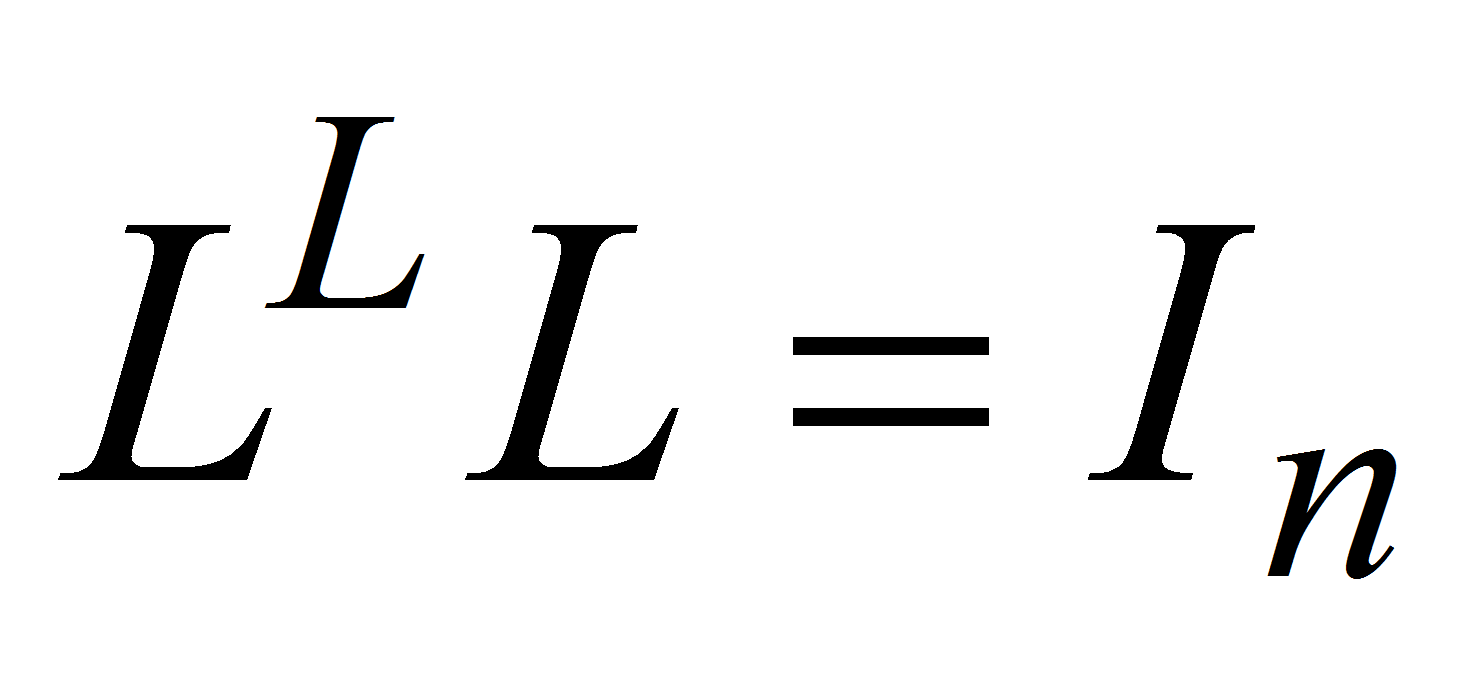 ).
).- Для определения параметров регулятора, воспользуемся утверждением, сформулированным В.Н. Буковым [10, с.473].
- Утверждение 1. Система (1) – (3) при заданных матрицах
 обладает инвариантностью к возмущениям
обладает инвариантностью к возмущениям
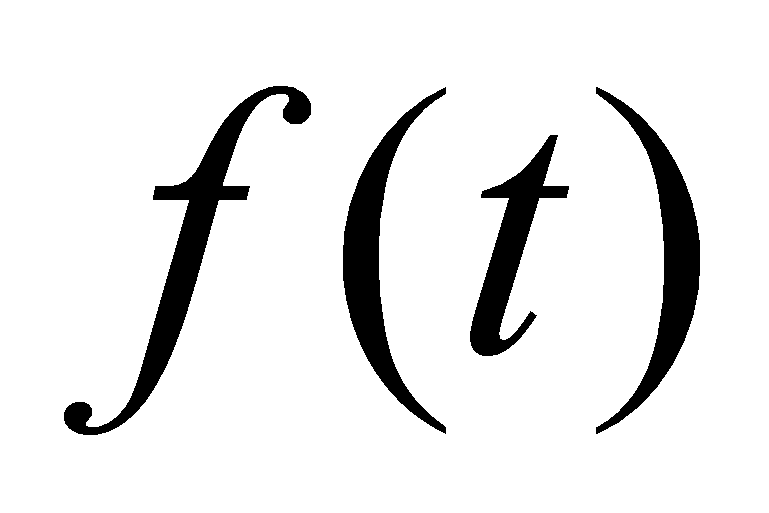 в смысле тождества
в смысле тождества
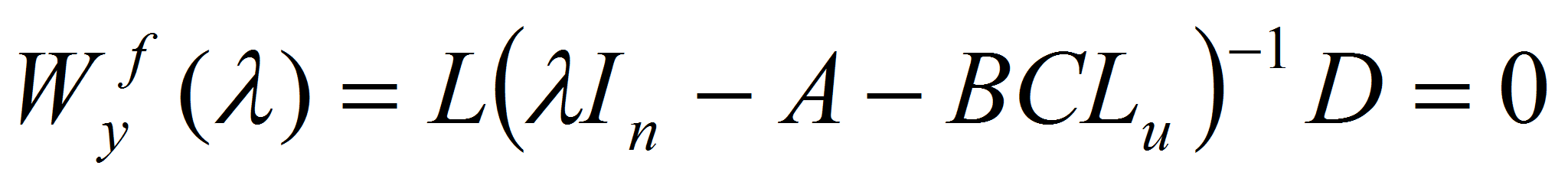
- тогда и только тогда, когда выполняются следующие условия:
- 1) существует ненулевая калибровочная матрица инвариантности
 ,
для которой выполняется условие
,
для которой выполняется условие
 ,
,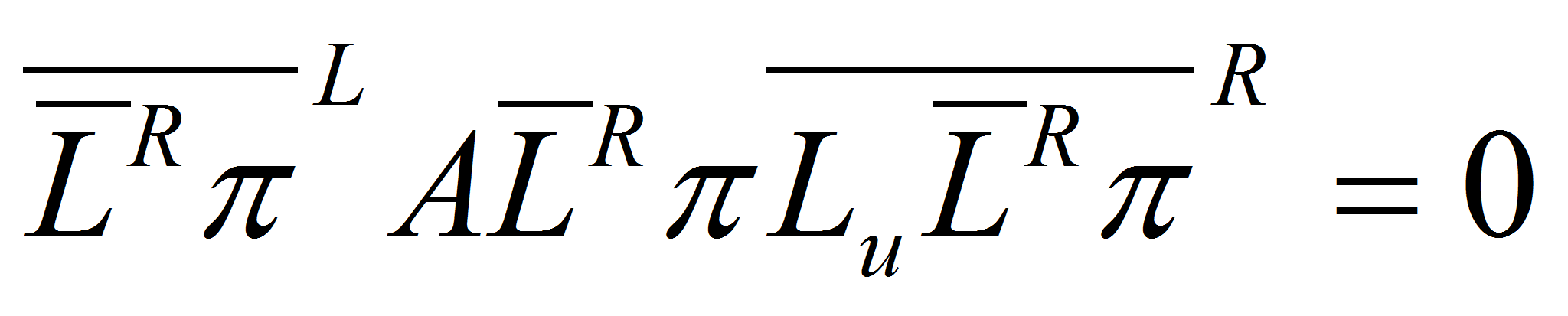 ;
;- 2) матрица эффективности возмущения принадлежит множеству
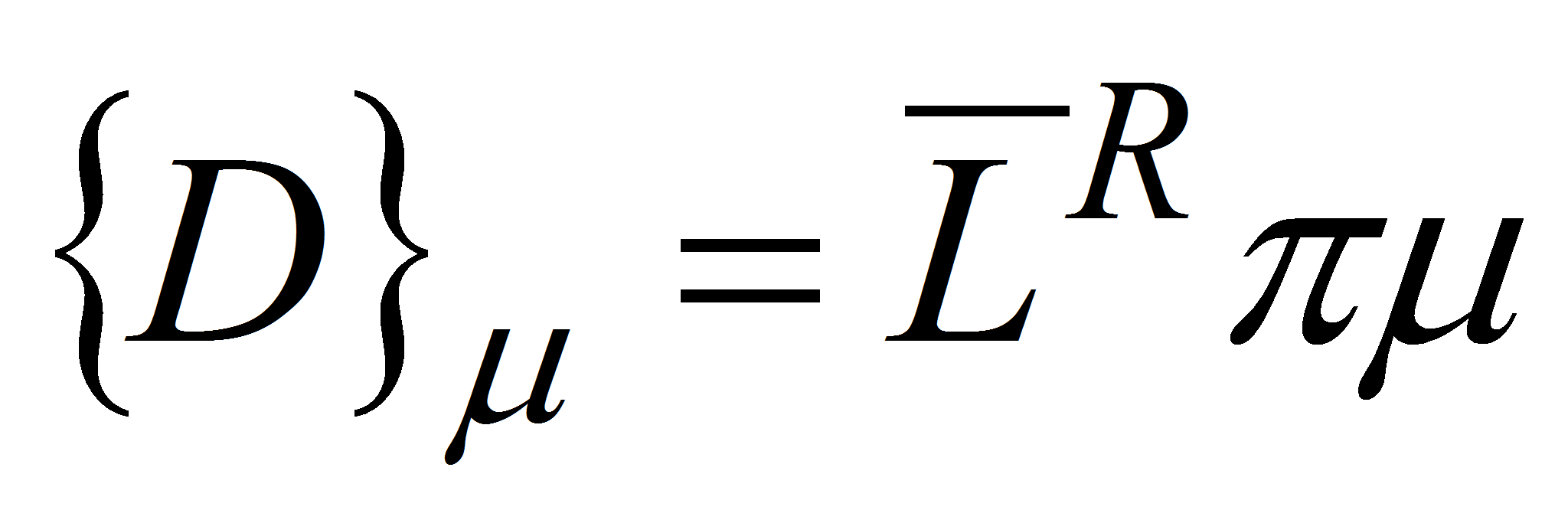 ,
,- где
 – произвольная числовая матрица подходящего размера;
– произвольная числовая матрица подходящего размера;- 3) система, замкнутая любым регулятором (6) из множества
- (6)
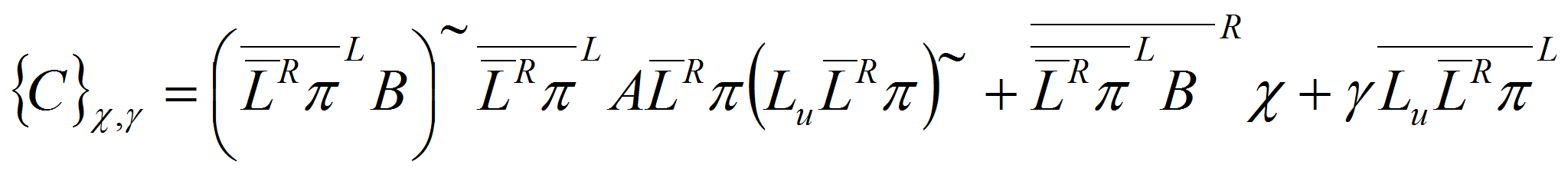 ,
,- где
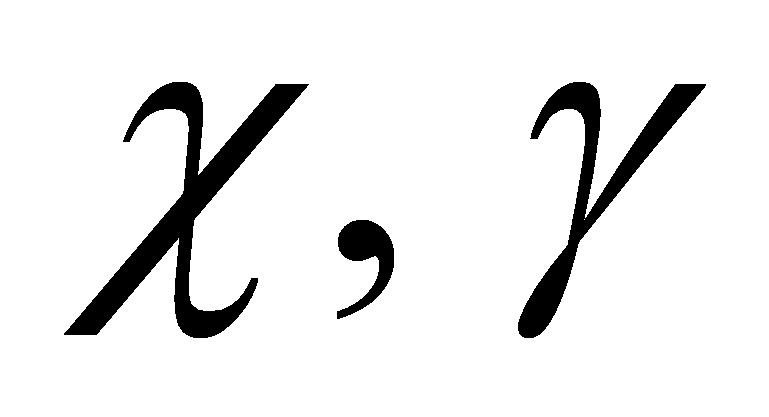 – матрицы подходящих размеров с произвольными элементами [10].
– матрицы подходящих размеров с произвольными элементами [10].
Синтез управления
- Используем закон управления (5), тогда уравнение
объекта (1) –
(3) примет вид
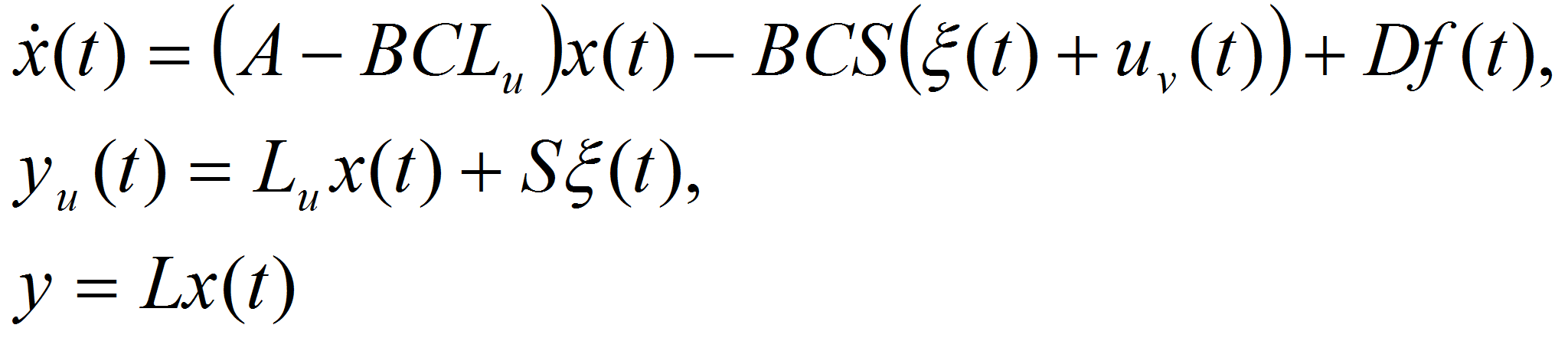 ,
,- где матрица
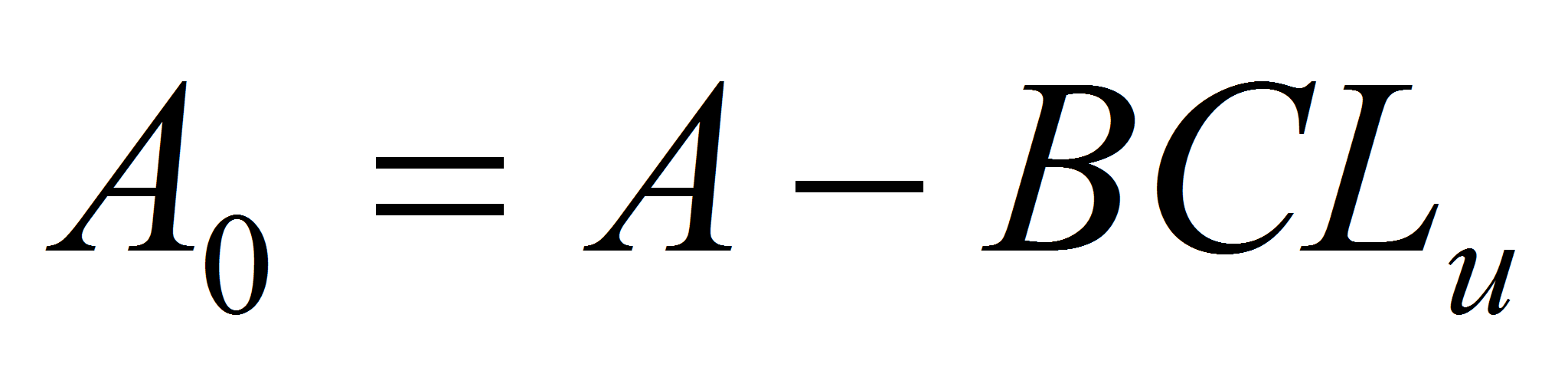 Гурвицева, то есть собственные числа удовлетворяют условию
Гурвицева, то есть собственные числа удовлетворяют условию
 .
С помощью технологии конструктивного вложения систем, определив
регулятор по формуле (6), мы добиваемся того, что передаточная
функция от возмущения к регулируемому выходу
.
С помощью технологии конструктивного вложения систем, определив
регулятор по формуле (6), мы добиваемся того, что передаточная
функция от возмущения к регулируемому выходу
 станет равна нулю, и, соответственно, компонента
станет равна нулю, и, соответственно, компонента
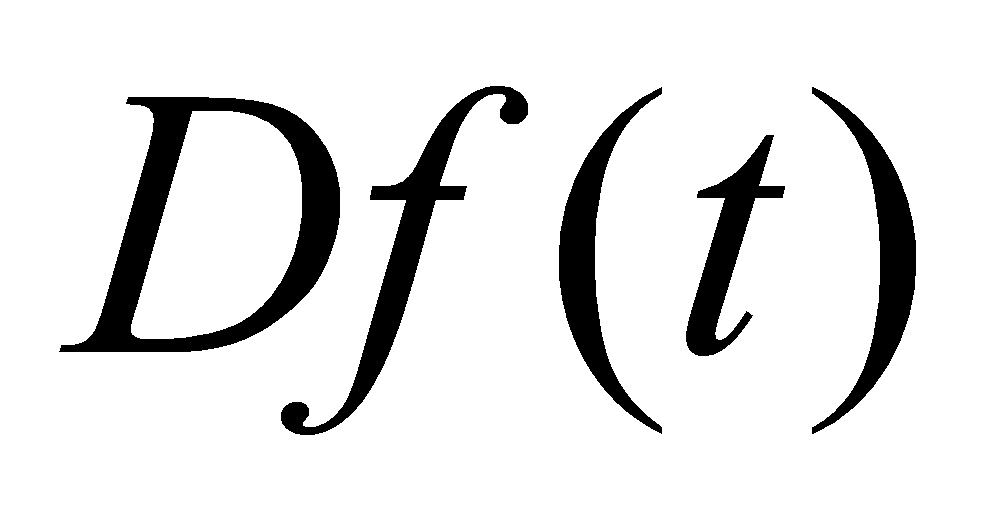 компенсируется. Далее перейдем к представлению системы в виде вход –
выход,
компенсируется. Далее перейдем к представлению системы в виде вход –
выход,- (7)
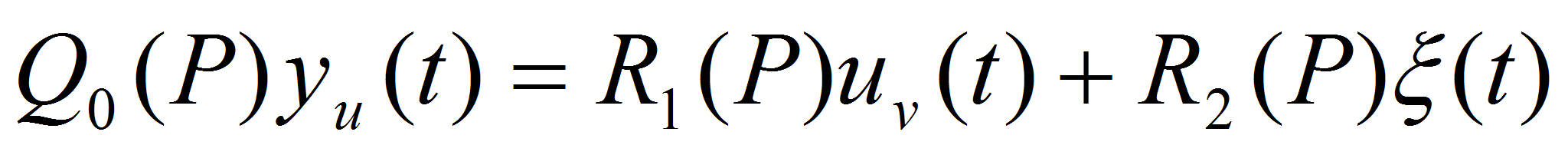
- где
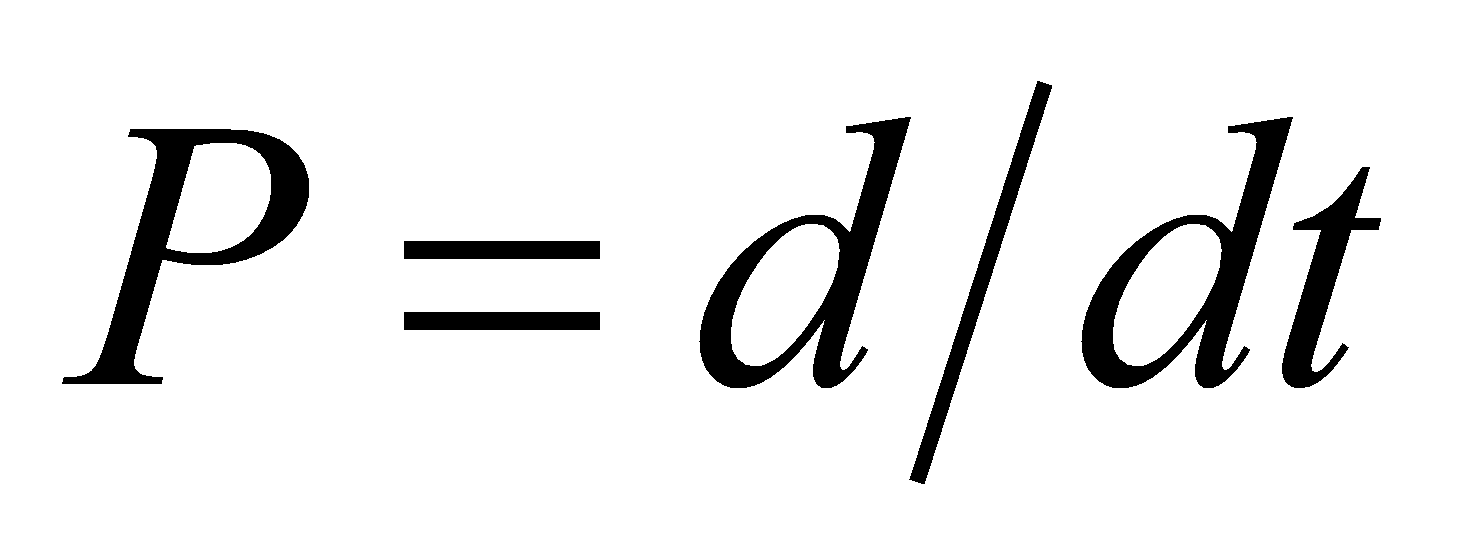 – оператор дифференцирования;
– оператор дифференцирования;
 ,
,
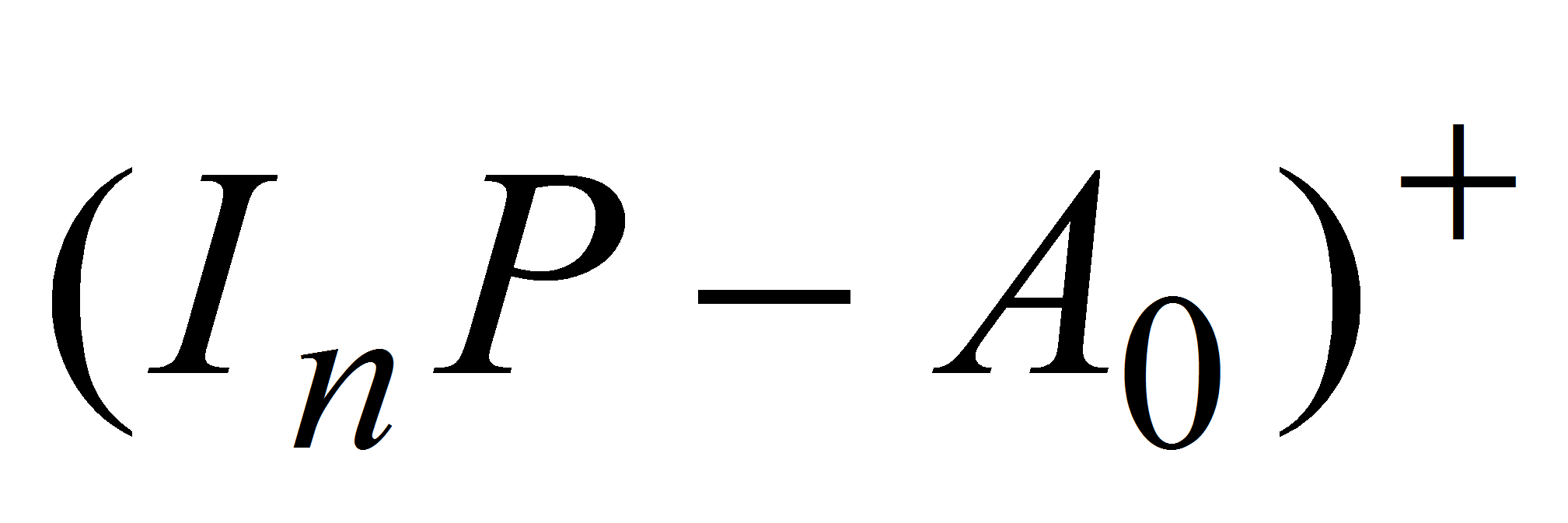 - транспонированная матрица алгебраических дополнений матрицы
- транспонированная матрица алгебраических дополнений матрицы
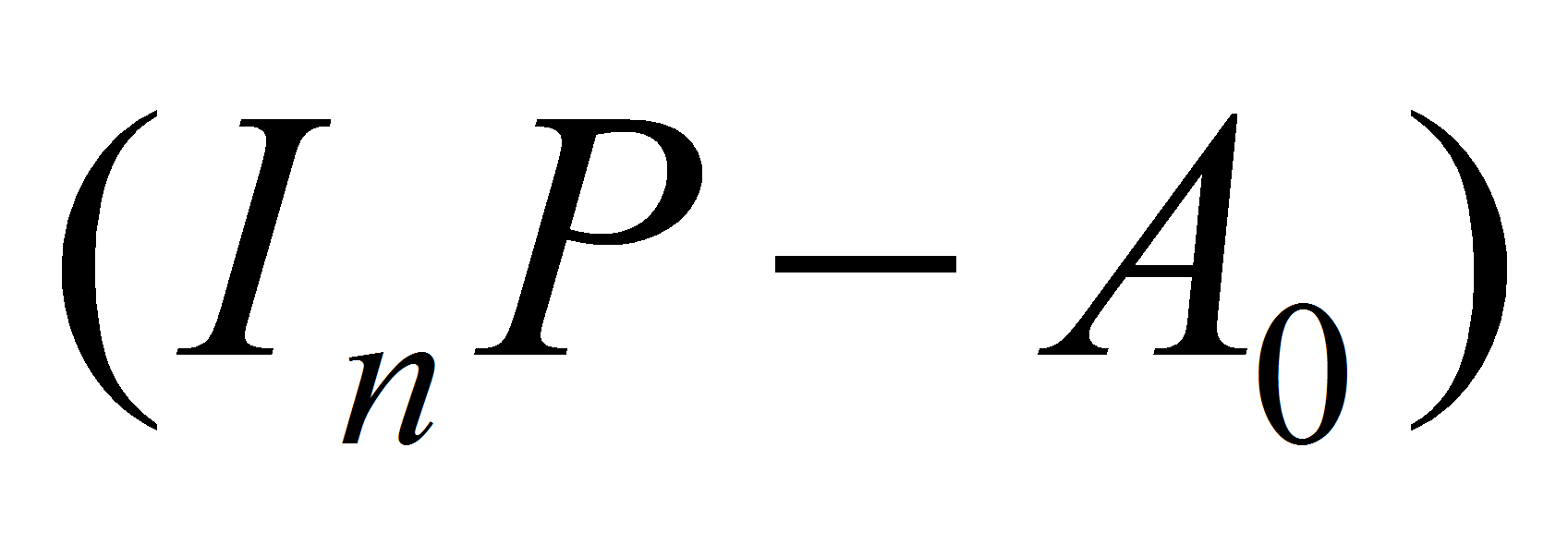 ;
;
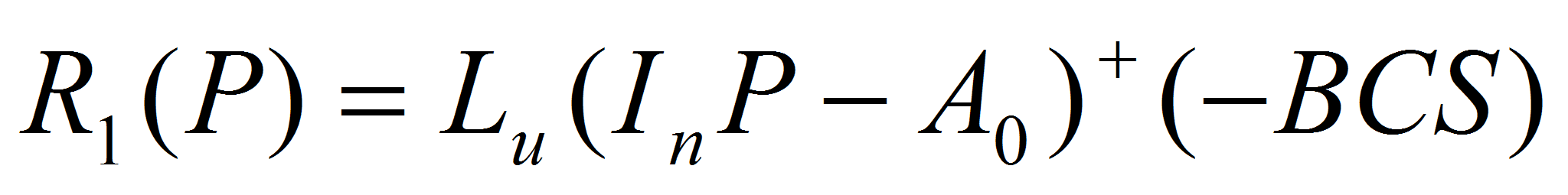 ,
,
 .
.
- Далее воспользуемся методом вспомогательного контура, и выделим сигнал, несущий информацию о помехах, для чего возьмем подсистему, которая описывается уравнением
- (8)
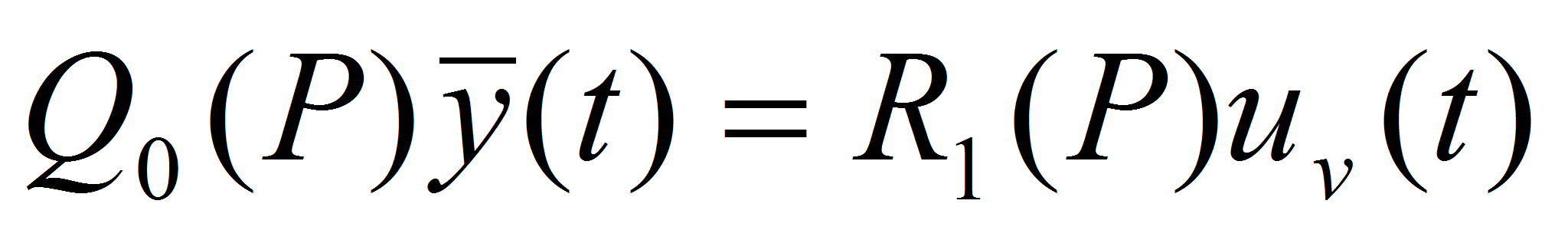 ,
,- и составим уравнение для сигнала рассогласования
 ,
вычитая (8) из (7):
,
вычитая (8) из (7):
- (9)
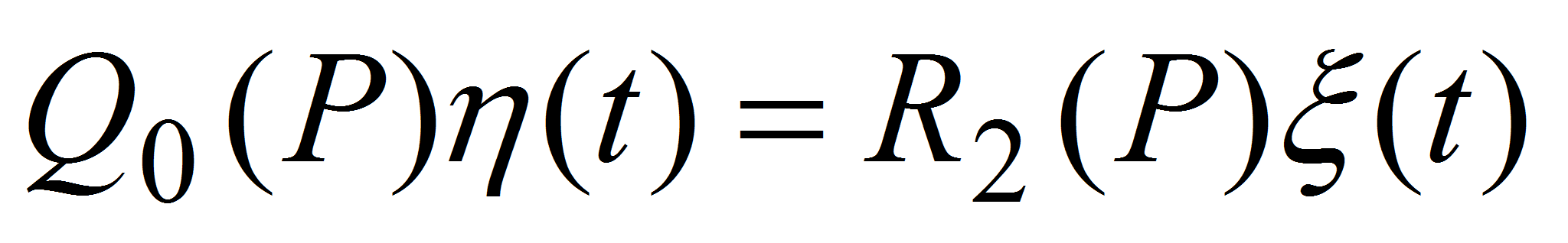 .
.- Из уравнения (9) выделим сигнал

- (10)
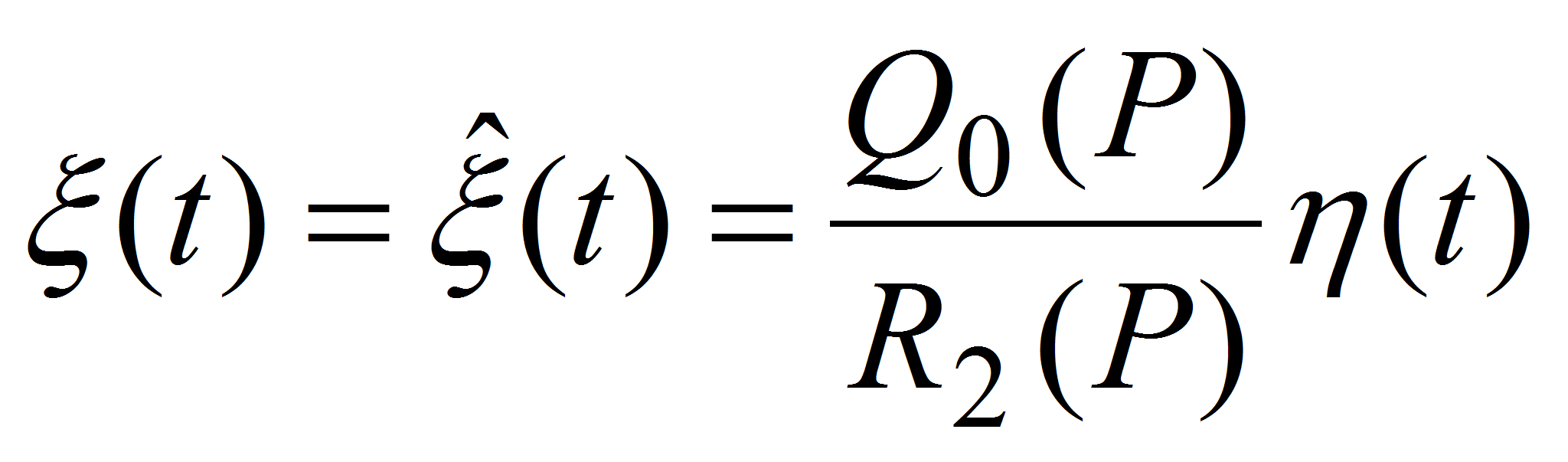 .
.- Для реализации (10) требуется гурвицевость полинома
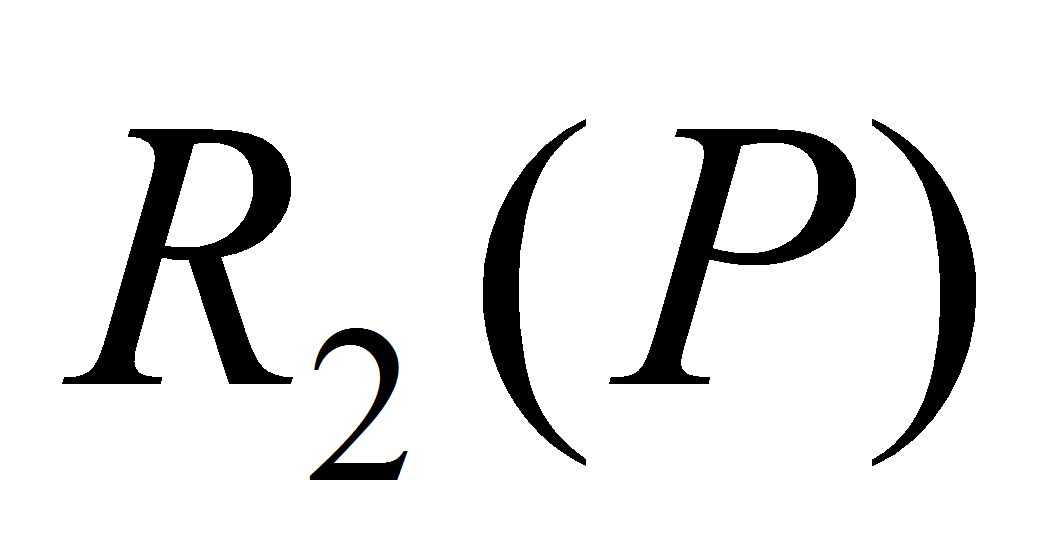 ,
что можно обеспечить соответствующим подбором матрицы
,
что можно обеспечить соответствующим подбором матрицы
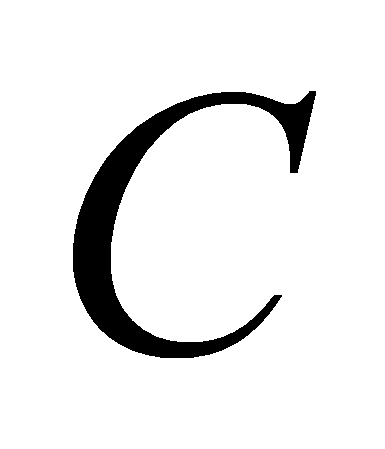 .
Однако такой подбор не всегда возможен. Таким образом, должна
существовать матрица
.
Однако такой подбор не всегда возможен. Таким образом, должна
существовать матрица
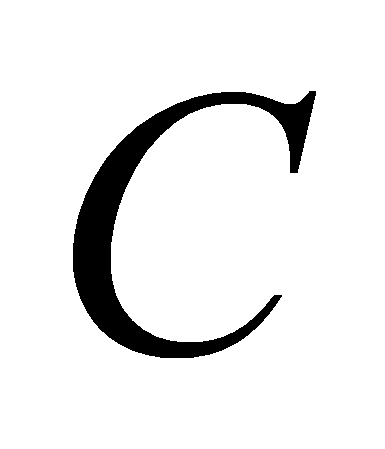 ,
обеспечивающая гурвицевость полиному
,
обеспечивающая гурвицевость полиному
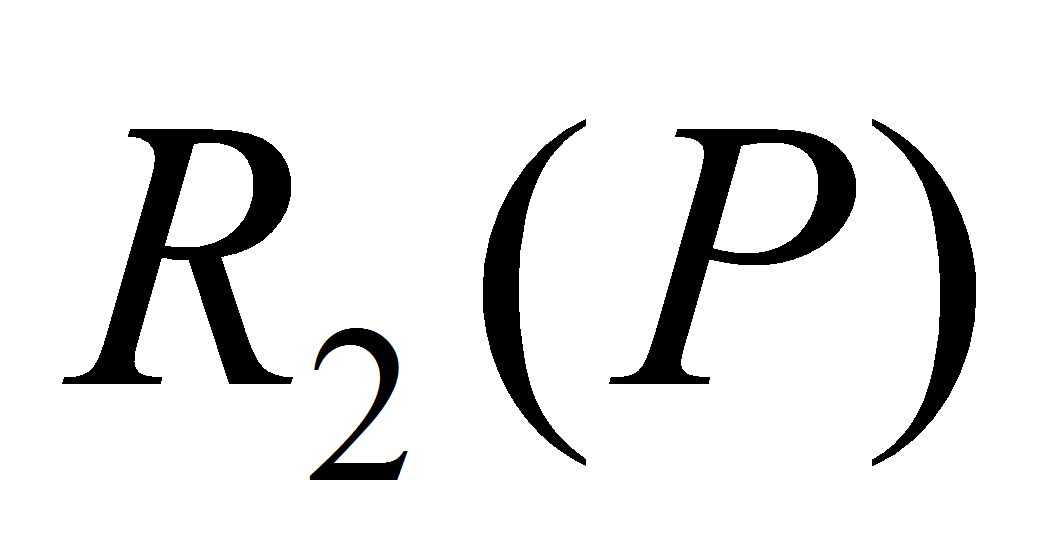 ,
что является дополнительным ограничением, не оговоренным в
предположении. Поскольку
,
что является дополнительным ограничением, не оговоренным в
предположении. Поскольку
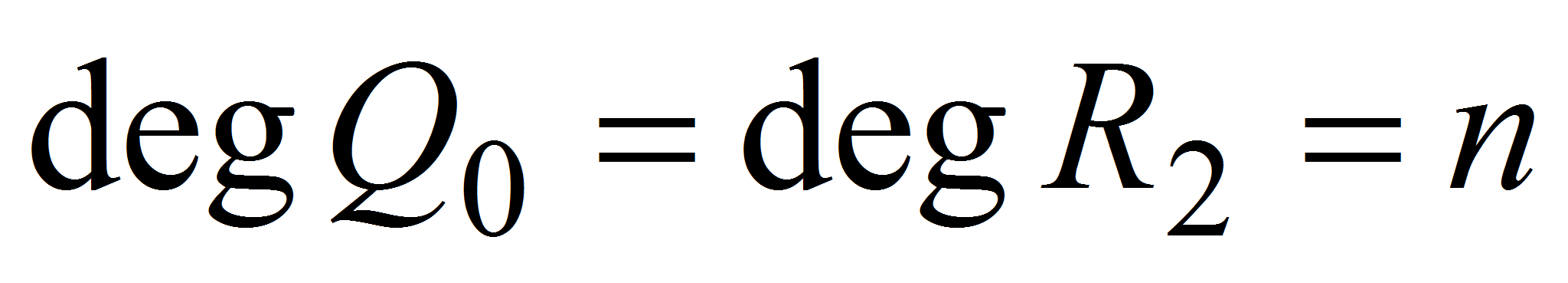 ,
то (9) реализуемо, и сформировав вспомогательный сигнал управления
,
то (9) реализуемо, и сформировав вспомогательный сигнал управления
 в виде
в виде- (11)
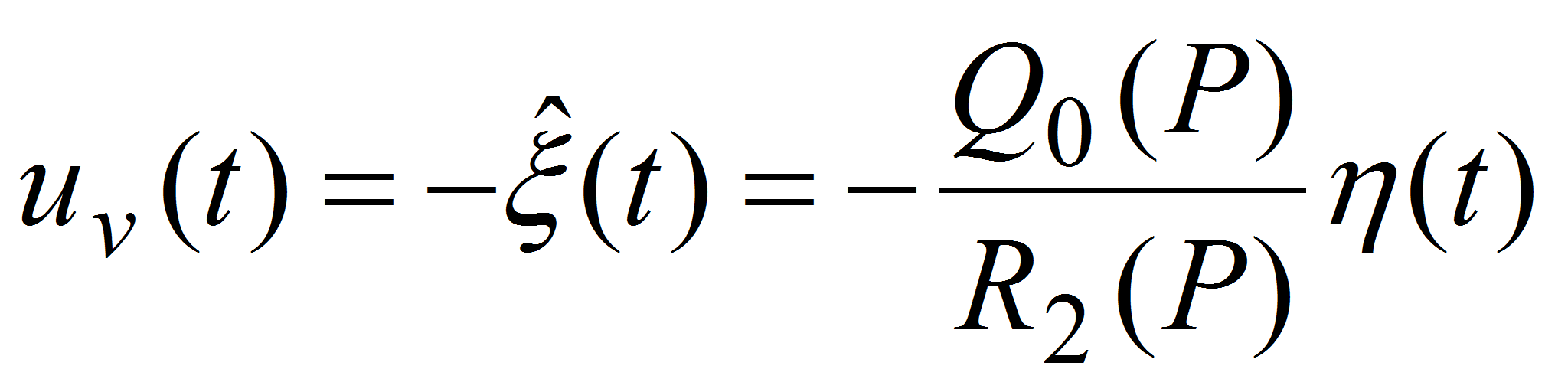
- получим уравнение для вектора состояния объекта
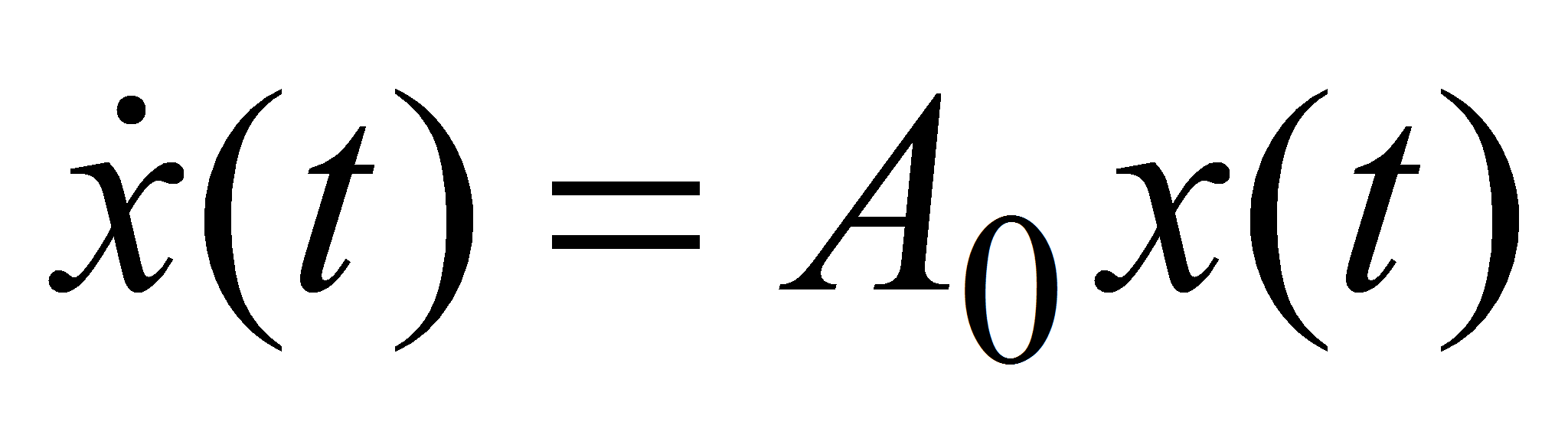 ,
,- Утверждение 2. Пусть выполнены условия предположений и существует матрица
 ,
обеспечивающая устойчивость числителя
передаточной функции (8). Тогда управляющее устройство, динамические
процессы в котором описываются уравнениями (5), (6), (8), (11)
обеспечивает выполнение целевого условия (4).
,
обеспечивающая устойчивость числителя
передаточной функции (8). Тогда управляющее устройство, динамические
процессы в котором описываются уравнениями (5), (6), (8), (11)
обеспечивает выполнение целевого условия (4).
Пример
- Рассмотрим задачу стабилизации для объекта
управления, динамические процессы в котором описываются уравнениями
(1) – (3).
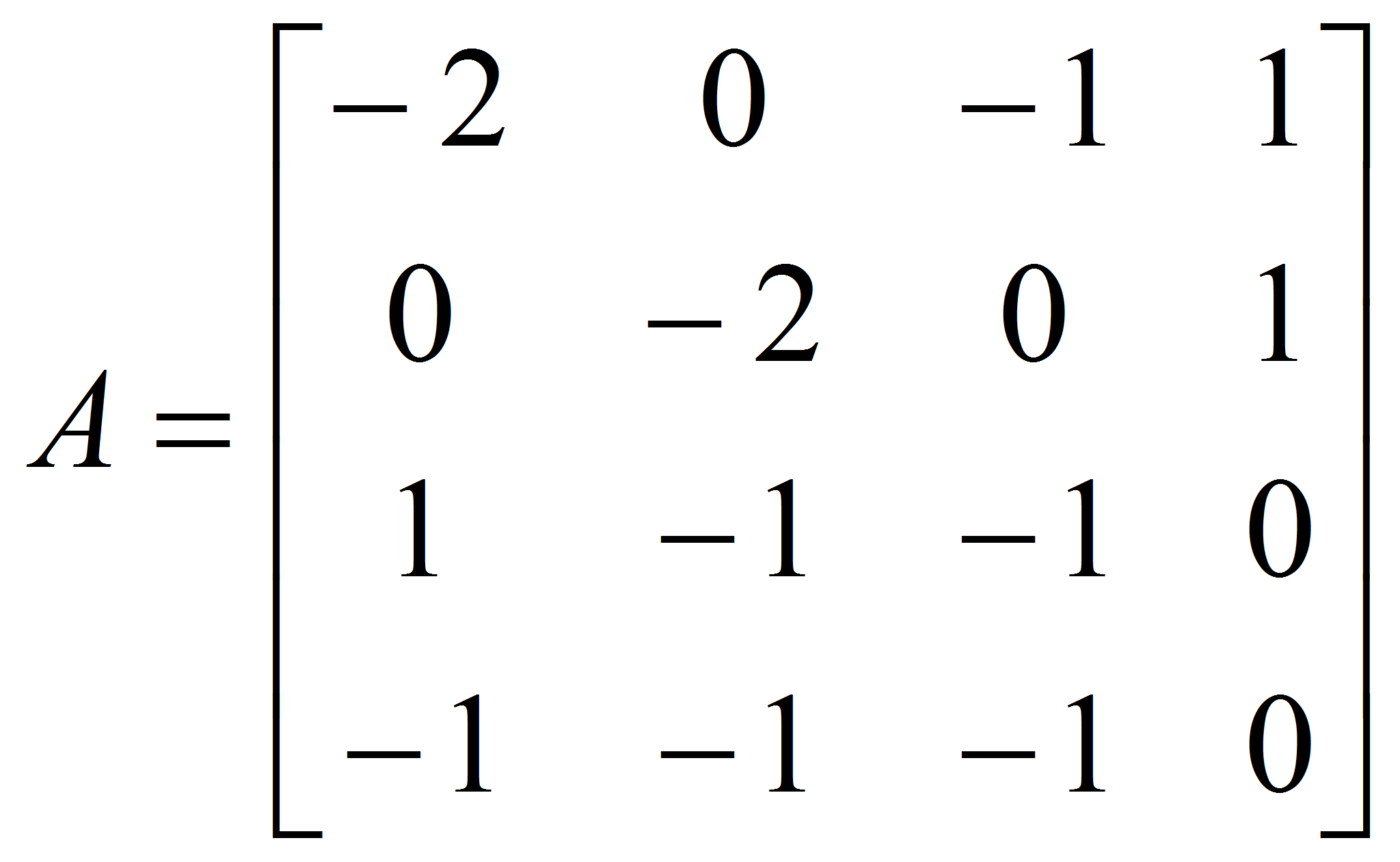 ,
,
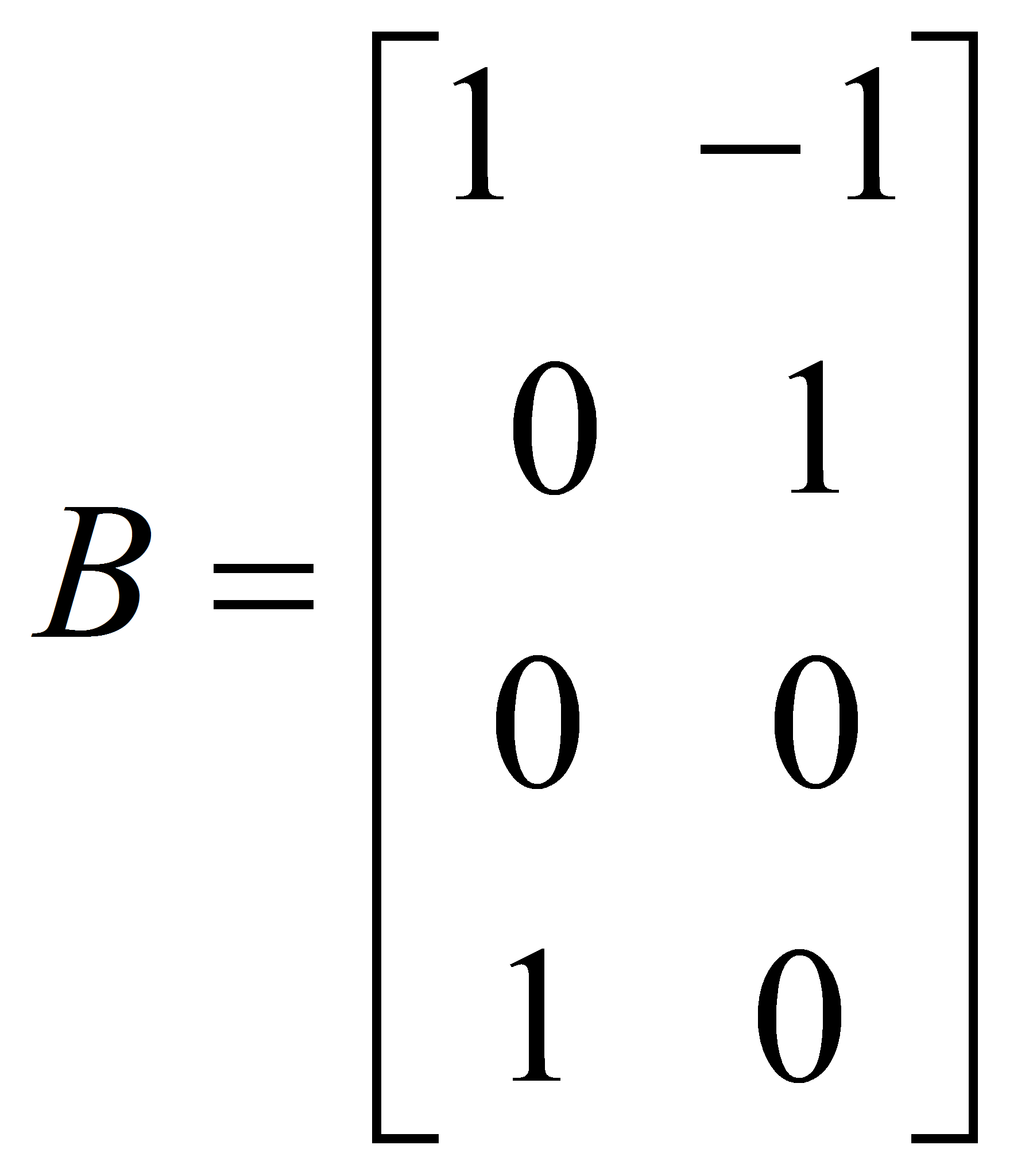 ,
,
 ,
,
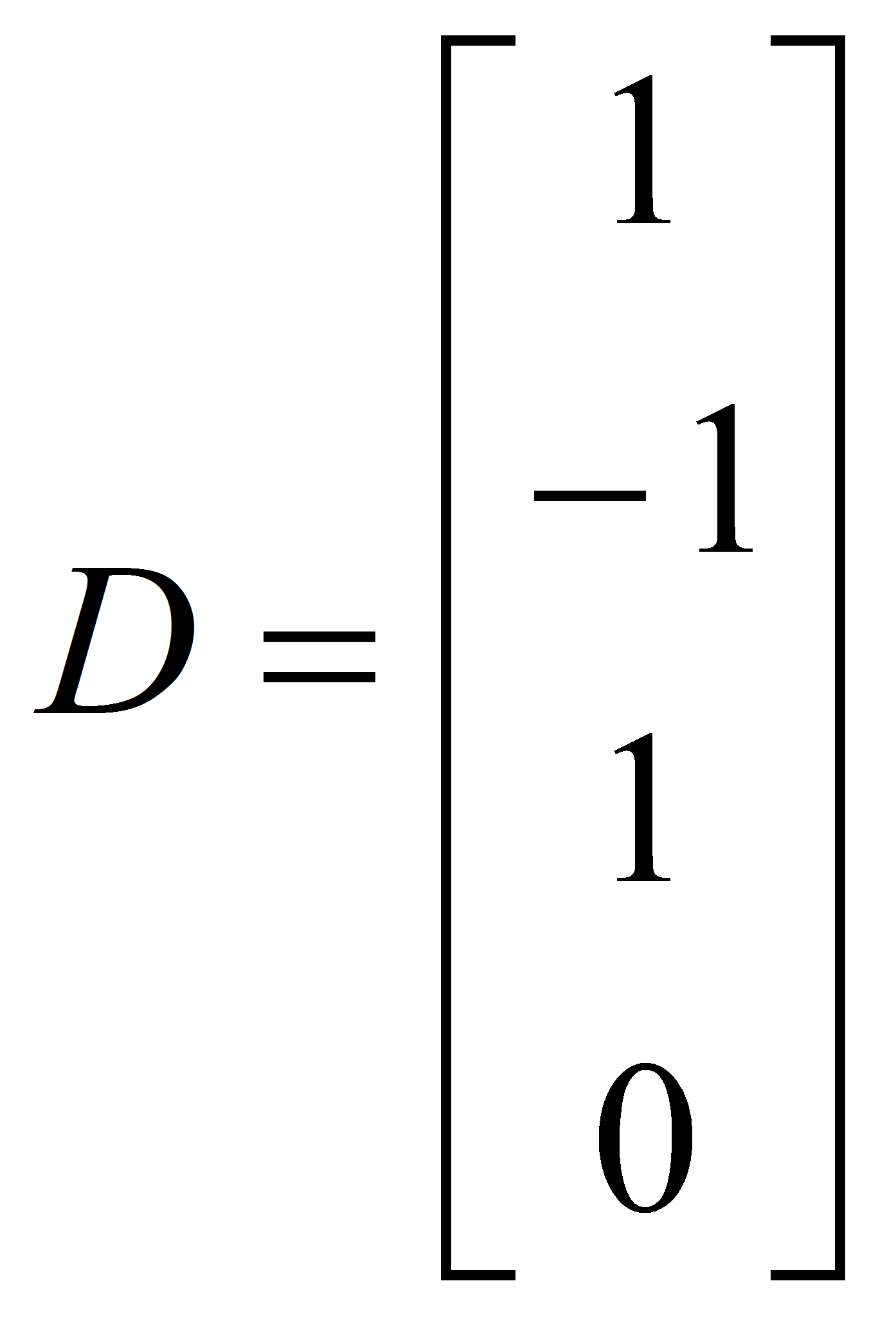 ,
,
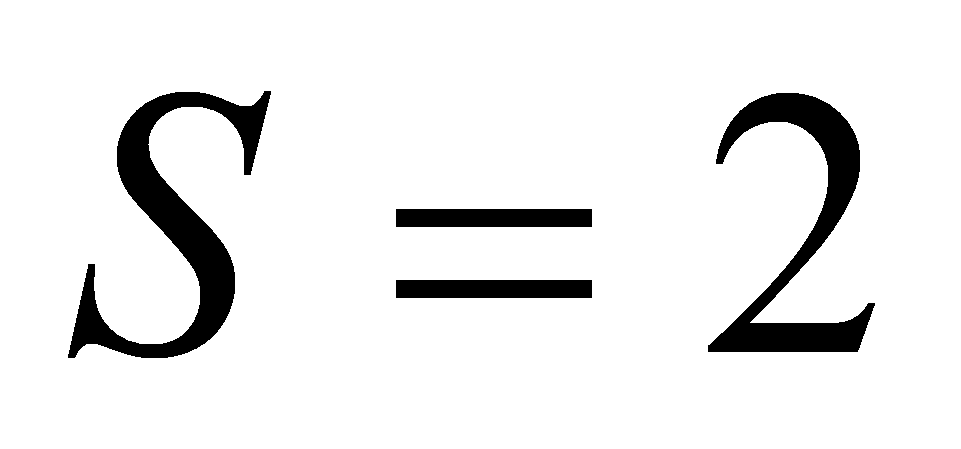 .
.- Формируем закон управления в виде
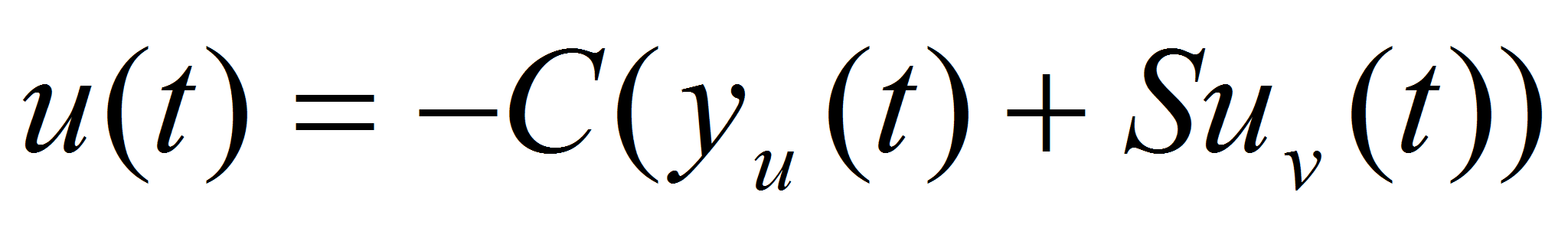 .
.
- Условия утверждения 1 выполняются. Для упрощения примем все варьируемые параметры равными нулю и получим следующую матрицу регулятора
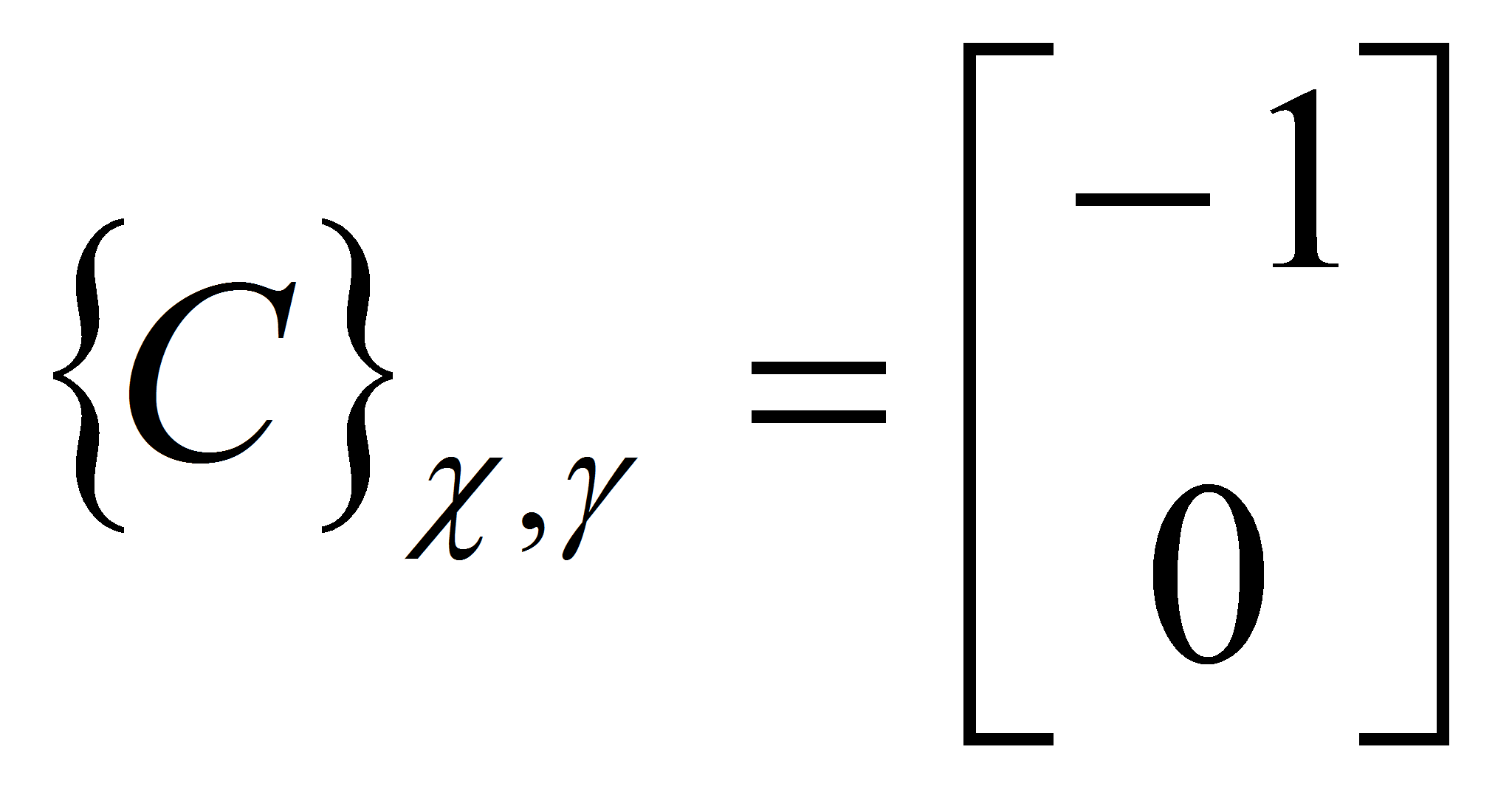
- Вспомогательное управляющее воздействие формируем в виде
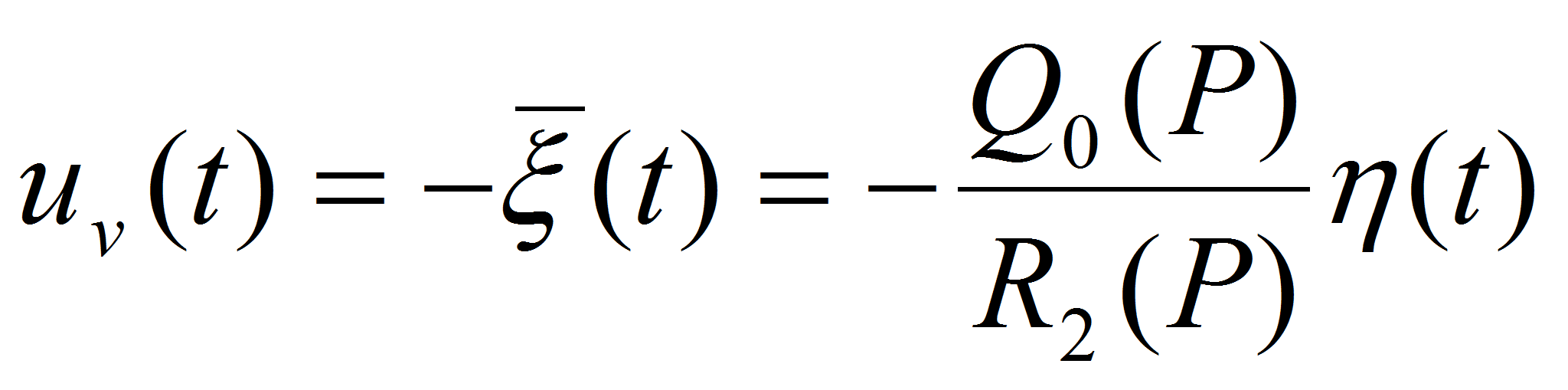 ,
,
- где
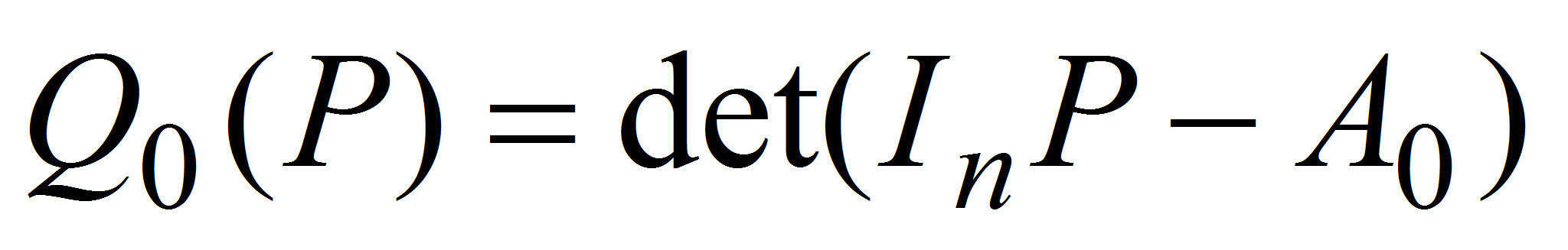 ,
,
 .
Для рассматриваемого примера получим следующее вспомогательное
управляющее воздействие
.
Для рассматриваемого примера получим следующее вспомогательное
управляющее воздействие
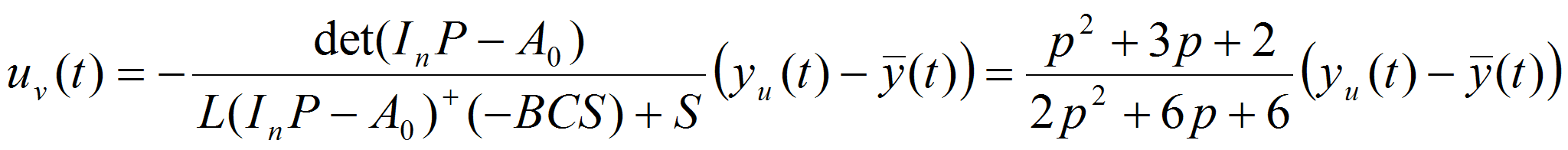 .
.- Тогда получим матрицу
 во вспомогательном контуре
во вспомогательном контуре
- На рис. 1 приведены результаты моделирования системы управления при следующих исходных данных: начальные условия
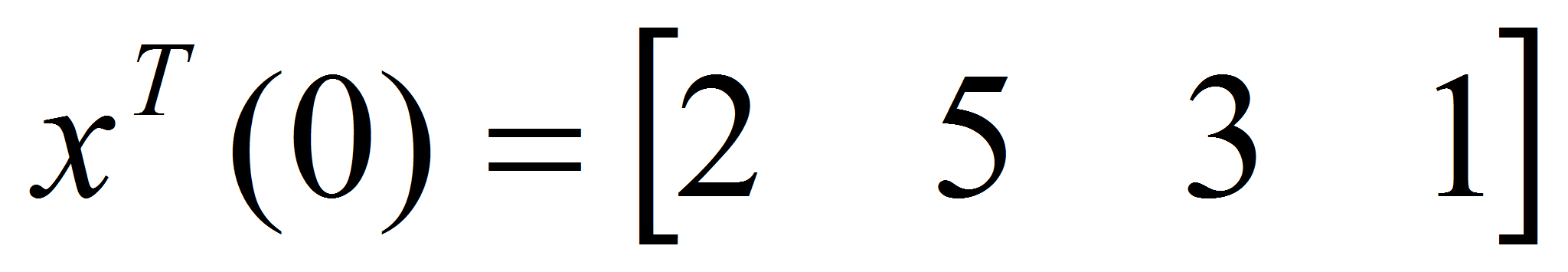 ,
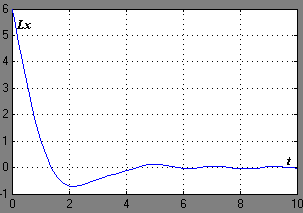
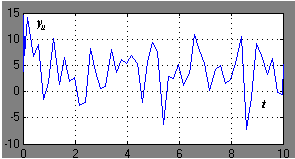
возмущающие воздействия на входе
,
возмущающие воздействия на входе
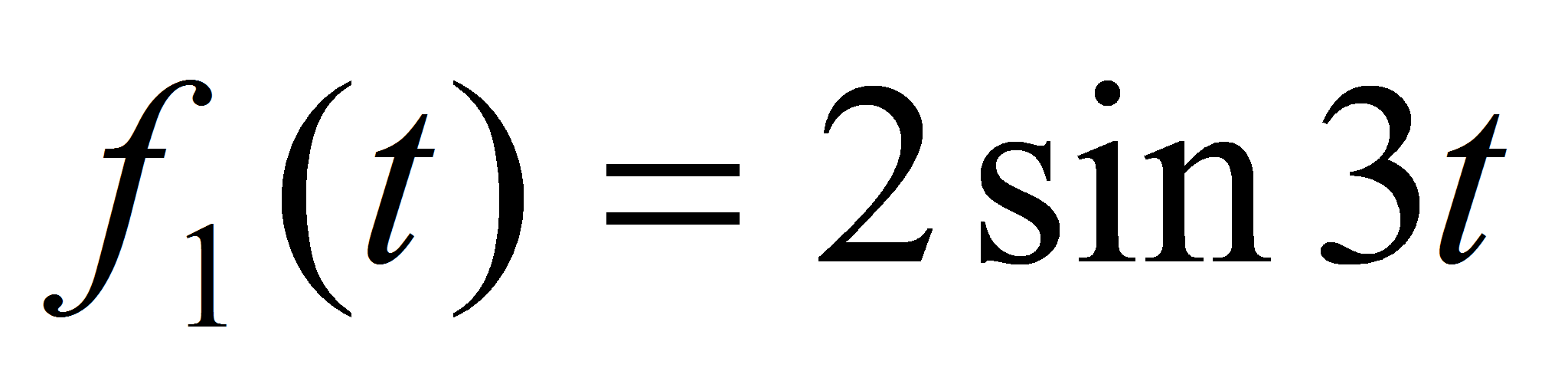 и
и
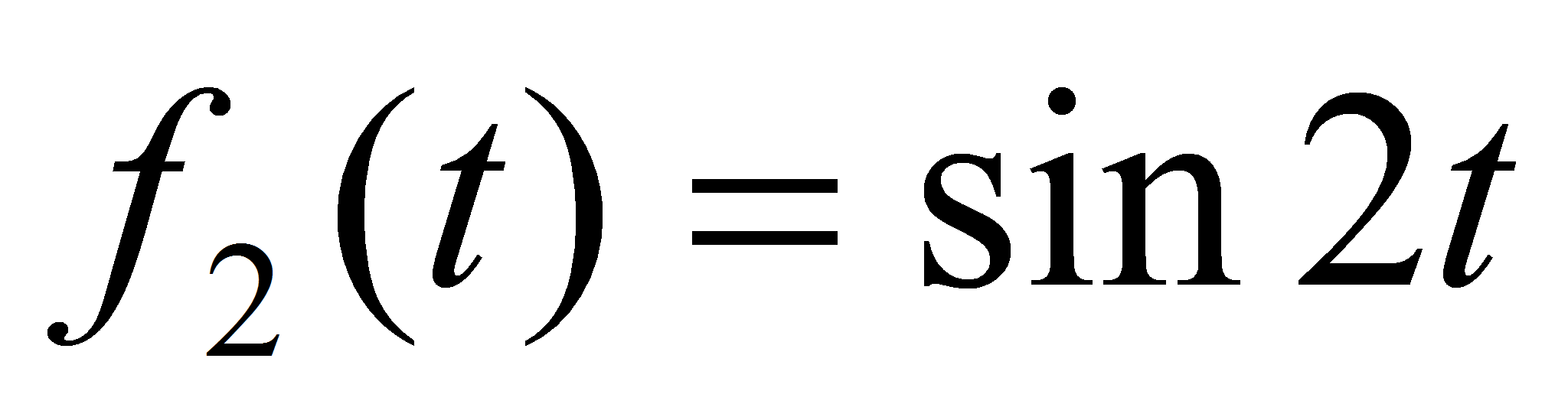 ,
шум на выходе представляет собой случайный сигнал.
,
шум на выходе представляет собой случайный сигнал.
Рис. 1. Переходные процессы в системе,
когда
![]() случайный сигнал
случайный сигнал
- В данном случае целевое условие выполняется через 8 секунд.
Заключение
- Решена задача построения робастной системы
управления линейным стационарным объектом без запаздываний и
каких-либо ограничений на управление, которая позволила
скомпенсировать возмущения на входе и на выходе системы, причем
возмущения эти различны. Спроектированная система управления
позволяет скомпенсировать влияние возмущения на регулируемые
переменные с заданной точностью, что продемонстрировано на примере.
Литература:
Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. – М.: Наука, 2002.
Никифоров В.О. Нелинейная система управления с компенсацией внешних детерминированных возмущений // Изв. РАН. Теория и системы управления. 1997. № 4. С. 69-73.
Бобцов А.А. Алгоритм робастного управления линейным объектом по выходу с компенсацией неизвестного детерминированного возмущения // Изв. РАН. Теория и системы управления. 2003. № 2. С. 93-97.
Никифоров В.О. Наблюдатели внешних возмущений. 1. Объекты с известными параметрами // АиТ. 2004. № 10. С. 13-24.
Никифоров В.О. Наблюдатели внешних возмущений. 1. Объекты с неизвестными параметрами // АиТ. 2004. № 11. С. 40-48.
Цыкунов А.М. Алгоритм робастного управления с компенсацией ограниченных возмущений // АиТ. 2007. № 7. С. 103-115.
Цыкунов А.М. Алгоритм робастного управления нестационарным объектом с компенсацией возмущений // Изв. РАН. Теория и системы управления. 2008. № 4. С. 33-40.
Цыкунов А.М. Алгоритм робастного управления линейным динамическим объектом // Мехатроника, автоматизация, управление. 2008. № 8. С. 7-12.
Цыкунов А.М. Компенсация возмущений и помех при децентрализованном управлении по косвенным измерениям // АиТ. 2010. № 4. С. 120-129.
Буков В.Н. Вложение систем. Аналитический подход к анализу и синтезу матричных систем. - Калуга: Изд-во науч. литературы Н.Ф. Бочкаревой, 2006.