Целью статьи является ознакомление с квантовым алгоритмом решения систем линейных алгебраических уравнений (СЛАУ) и программой для его моделирования на ЭВМ с помощью программы MATLAB. В работе представлен код программы модели и результат её работы.
Ключевые слова: квантовый компьютер, кубит, квантовый алгоритм, собственное число, собственное значение, матрица, СЛАУ.
Квантовые технологии уже изменили повседневную жизнь. Компьютеры, мобильные телефоны, медицинские изображения, лазеры и сверхпроводники — все это появилось в результате научной революции начала двадцатого века, когда физики открыли внутреннюю работу атома с помощью квантовой механики. Такие квантовые технологии включают в себя невзламываемое шифрование, сверхчувствительные сенсоры и новые способы обработки изображений.
На протяжении десятилетий вычислительная мощность ЭВМ росла в соответствии с законом Мура. Размеры транзисторов приблизились к размеру атома, из-за чего на их работе сказываются квантовые эффекты. Это технологическое ограничение послужило толчком к переходу к другой парадигме вычислений, развитию квантовой информатики и к созданию квантового компьютера. [1, 2]
Квантовые компьютеры — это устройства, которые используют для вычислений принципы квантовой механики. Для некоторых задач квантовые алгоритмы обеспечивают существенное ускорение по сравнению с их лучшим классическим аналогом. [2] Этим объясняется интерес к квантовым компьютерам со стороны как технологических гигантов, так и ведущих стран: Великобритании, Германии, Израиля, Канады, Китая, Нидерландов, России, США, Франции, Японии. Кроме того, наблюдается постоянное расширение поля исследований квантовых вычислений и квантовых технологий в целом по всему миру.
Наряду с государственными инвестициями сотни компаний инвестируют в эту область и проводят собственные исследования: IBM, Google, Alibaba, Hewlett Packard, Tencent, Baidu и Huawei. Компания Google в настоящее время создала квантовый процессор на 53 кубитах под названием «Sycamore», который может решать специализированные задачи за 200 секунд, на что суперкомпьютеру потребовалось бы 10 000 лет. [3] Безопасное шифрование с использованием квантовой технологии уже является коммерческим продуктом. Квантовый компьютер так же стал доступен как коммерческий продукт, например, канадская фирма «D-Wave Systems» продает квантовые компьютеры D-Wave. Эти машины специализируются на конкретных задачах, известных как проблемы оптимизации. Эта фирма привлекла 177 миллионов долларов.

Рис. 1. Квантовые процессоры Intel. Слева направо: 7, 17 и 49 кубитов
В начале 2019 года на выставке CES 2019 в Лас-Вегасе был презентован ещё один коммерческий квантовый компьютер Q System One от IBM на 20 кубитах. Эта вычислительная машина заключена в огромную герметичную камеру, которая охлаждается сверху вниз: в самой нижней части температура составляет 4 Кельвина (-269,15 градусов Цельсия), в нижней — 10 милликельвинов.

Рис. 2. Квантовый компьютер IBM Q System One
Ещё одним признаком высокого интереса к квантовым технологиям является патентная активность. Патентный анализ показывает, что одной из самых активных стран является Китай. По данным, полученным Объединенным исследовательским центром Европейской комиссии в городе Испра (Италия) более 43 % инноваций в области квантовых технологий, запатентованных в период с 2012 по 2017 годы, были получены китайскими фирмами и университетами. [4]
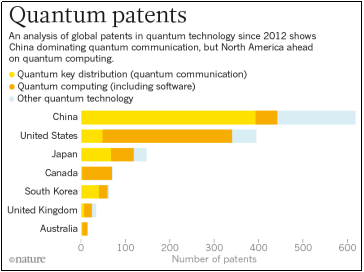
Рис. 3. Патенты на квантовые технологии в мире
Государственные программы финансирования квантовых разработок под названием «Квантовый флагман» в Евросоюзе, впервые был объявлен в 2016 году, собрали €1 млрд. Более 20 международных консорциумов, каждый из которых включает государственные научно-исследовательские институты и промышленность, получат в общей сложности 132 миллиона евро в течение 3 лет для демонстрационных технологических проектов. [5]
В России в последние годы уделяется много внимания развитию квантовых технологий на высшем уровне. Так, президент РФ Путин В. В. в своем ежегодном послании федеральному собранию в 2016 году сказал: «Нам нужны собственные передовые разработки и научные решения. Цифровые технологии, другие так называемые сквозные технологии, которые сегодня определяют облик всех сфер жизни. Страны, которые смогут их генерировать, будут иметь долгосрочное преимущество. Другие окажутся в зависимом, уязвимом положении. Это цифровые, квантовые технологии, робототехника, нейротехнология. В цифровых технологиях кроются и риски. Необходимо укреплять киберзащиту. Развитие цифровой экономики, в её реализации будем опираться именно на российские компании». [6]
В национальном исследовательском технологическом университете (НИТУ «МИСиС») работает первая в России лаборатория, которая стала выполнять измерения кубитов при сверхнизких температурах. При поддержке этого университета российский квантовый центр (РКЦ) открыл первую школу по квантовым коммуникациям в образовательном центре «Сириус».
Над созданием элементов квантового компьютера, — кубитов — работают МГУ, МФТИ, НИТУ «МИСиС», НОЦ ФМН, ФИАН, РКЦ и ряд других организаций.

Рис. 4. Криостат квантового компьютера, собранного в НИТУ «МИСиС»
Весной 2019 года стало известно, что РКЦ и НИТУ «МИСиС» разработали проект «дорожной карты» развития квантовых технологий в рамках федеральной программы «Цифровая экономика». В соответствии с проектом, к 2024 году должно быть сокращено отставание страны в этой области, для чего предполагалось создать профильную организацию и выделить более 43 млрд. рублей. Также, в соответствии с этим проектом, в ноябре 2019 года госкорпорация «Росатом» запустила проект по созданию отечественного квантового компьютера с финансированием объемом в 24 млрд. рублей. [7]
Исследователи из ИТМО создали систему квантовой связи для защищённой передачи данных на основе принципиально нового подхода. Система позволит передавать данные на расстояния более 250 километров, что не уступает самым современным зарубежным устройствам.
В развитии квантовых технологий заинтересованы и военные. Военный инновационный технополис «ЭРА» в Анапе предназначен для поиска, развития и внедрения прорывных технологий в оборонной сфере. На базе его мощностей предполагается освоение в том числе и квантовых технологий, и работа над квантовыми алгоритмами [8].
Одним из таких квантовых алгоритмов является квантовый алгоритм решения систем линейных алгебраических уравнений. Системы линейных уравнений играют важную роль в различных областях, начиная от естественных наук и техники до медицины и обществознания.
Решение СЛАУ лежит в основе многих современных технологий, в том числе анализ сетевого трафика, компьютерная томография и прогнозирование погоды. С ростом объёма входных данных для их численного моделирования растут требования к вычислительной мощности ЭВМ. Объем данных в некоторых случаях может достигать порядка терабайт и даже петабайт. Таким образом, задача численного эксперимента для таких систем может быть препятствием даже для новейших суперкомпьютеров. В лучшем случае требование к ресурсам классического компьютера при решении таких задач пропорциональна количеству переменных в данной СЛАУ. Данный квантовый алгоритм позволяет в некоторых случаях получить экспоненциальное ускорение [9], а также может быть лучше известного численного метода решения СЛАУ на ЭВМ — метода сопряженных градиентов.
![]()
Кроме того, учитывая такой процесс как дискретизация дифференциальных уравнений, при котором они преобразовываются в систему алгебраических уравнений, проблематика СЛАУ может быть расширена и на случаи численных методов решения диффуров.
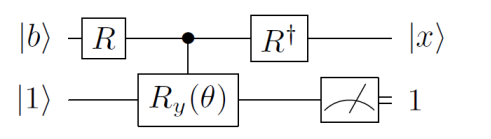
Рис. 5. Квантовая схема алгоритма решения СЛАУ
В данной работе представлено описание квантового алгоритма решения СЛАУ, а также код программы MATLAB для моделирования его работы.
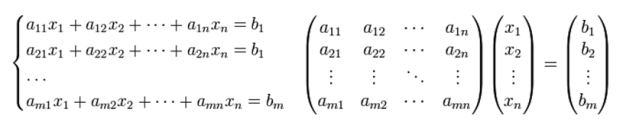
Пусть, дана квадратная система линейных алгебраических уравнений. Её матричное представление состоит из симметричной матрицы ![]() размера N x N с коэффициентами
размера N x N с коэффициентами ![]() , вектор-столбца неизвестных
, вектор-столбца неизвестных ![]() и вектор-столбца свободных членов
и вектор-столбца свободных членов ![]() .
.
С помощью квантового алгоритма необходимо найти решение уравнения ![]() , такое что
, такое что ![]() .
.
Алгоритм можно разделить на 2 части. Так как квантовый алгоритм «напрямую» не оперирует элементами матрицы A и вектор-столбца свободных членов ![]() , то сначала, на первом этапе, происходит преобразование матрицы A в соответствующий ей квантовый оператор (гейт). Также, происходит преобразование вектор-столбца свободных членов
, то сначала, на первом этапе, происходит преобразование матрицы A в соответствующий ей квантовый оператор (гейт). Также, происходит преобразование вектор-столбца свободных членов ![]() в соответствующее ему квантовое состояние (кет-вектор
в соответствующее ему квантовое состояние (кет-вектор ![]() ). Второй этап заключается в выполнении вычисления по квантовой схеме (рис. 5) и получение ответа.
). Второй этап заключается в выполнении вычисления по квантовой схеме (рис. 5) и получение ответа.
У алгоритма существуют ограничения и поэтому не всякую матрицу A и не всякий вектор-столбец ![]() можно преобразовать. Так, к примеру, векторы
можно преобразовать. Так, к примеру, векторы ![]() и
и ![]() должны быть нормированы, т. е.
должны быть нормированы, т. е. ![]() . Это необходимое условие для преобразования указанных вектор-столбцов в соответствующие им квантовые состояния
. Это необходимое условие для преобразования указанных вектор-столбцов в соответствующие им квантовые состояния ![]() и
и ![]() .
.
На квантовой схеме предполагается, что вектор-столбец ![]() уже преобразован в квантовое состояние
уже преобразован в квантовое состояние ![]() . Также предполагается, что данная схема может быть подпрограммой, которой на вход, в качестве параметра, передается этот кет-вектор.
. Также предполагается, что данная схема может быть подпрограммой, которой на вход, в качестве параметра, передается этот кет-вектор.
В результате преобразования вектора ![]() в квантовое состояние
в квантовое состояние ![]() должен быть получен следующий кет-вектор
должен быть получен следующий кет-вектор ![]() , где
, где ![]() — амплитуды вероятности при базисных состояниях
— амплитуды вероятности при базисных состояниях ![]() .
.
Обозначим множество квантовых состояний, представляющих собственные векторы матрицы А как ![]() и множество её собственных значений как
и множество её собственных значений как ![]() .
.
Следующий шаг — разложение квантового состояния ![]() в базисе собственных векторов
в базисе собственных векторов ![]() :
:
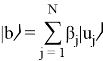
где ![]() .
.
Результирующее квантовое состояние
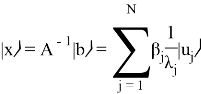
Описание следующих 3 шагов: оценка фазы (оператор R), управляемое вращение (оператор ![]() ) и инверсия оценки фазы (оператор
) и инверсия оценки фазы (оператор ![]() ). Оценка фазы используется для определения собственных значений
). Оценка фазы используется для определения собственных значений ![]() матрицы A и разложения квантового состояния в определенном базисе.
матрицы A и разложения квантового состояния в определенном базисе.
Рассмотрим каждый из выше описанных операторов подробнее. Оператор R представляет собой квадратную матрицу, столбцами которой являются собственные векторы матрицы A. Собственный вектор — это ненулевой вектор, применение к которому матрицы A даёт коллинеарный вектор (тот же вектор, умноженный на некоторое число). Собственный вектор — это такой ненулевой вектор ![]() , что для некоторого
, что для некоторого ![]() должно выполняться следующее равенство:
должно выполняться следующее равенство:
![]() ,
,
где ![]() — данная матрица,
— данная матрица, ![]() — собственный вектор матрицы
— собственный вектор матрицы ![]() ,
, ![]() — это скаляр, собственное значение (его описание приведено ниже), существующее для данного собственного вектора.
— это скаляр, собственное значение (его описание приведено ниже), существующее для данного собственного вектора.
Оператор R может быть представлен в следующем виде:
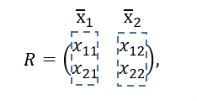
где ![]() и
и ![]() — это собственные векторы матрицы
— это собственные векторы матрицы ![]() :
: ![]() и
и ![]() соответственно.
соответственно.
После оператора R следует оператор вращения ![]() . Оператор вращения предназначен для представления в «квантовом виде» собственных значений данной матрицы A с их последующим преобразованием в угол поворота вектора состояния.
. Оператор вращения предназначен для представления в «квантовом виде» собственных значений данной матрицы A с их последующим преобразованием в угол поворота вектора состояния.
Данное преобразование состоит из двух операторов: оператора CNOT и оператора вращения
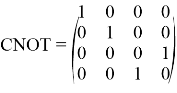
Оператор вращения для одного кубита имеет вид:
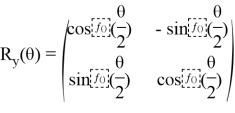
Матрица поворота в двумерном пространстве широко используется в линейной алгебре для описания преобразований векторов.
Оператор вращения ![]() имеет вид:
имеет вид:
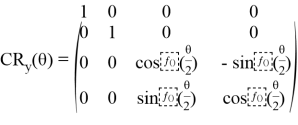 ,
,
где ![]() , а
, а ![]() — собственные значения матрицы A.
— собственные значения матрицы A.
Оператор ![]() — является транспонированной матрицей оператора
— является транспонированной матрицей оператора ![]() .
.
Результатом работы программы является вектор-столбец:
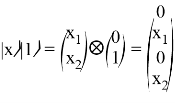 ,
,
где
Описание программы моделирования
Пусть, дана система уравнений:
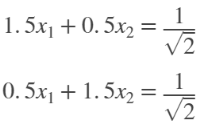
- Инициализация переменных со входными данными (матрица (A), кет-вектор свободных членов b, единичная матрица I) и оператора измерения M:

- Вычисление собственных векторов и собственных значений матрицы A и запись их в переменные R и eigenvals соответственно:

- Запись в переменную Rt результата транспонирования матрицы собственных векторов матрицы A:

-
Вычисление угла поворота
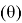 для оператора вращения как отношение собственных значений матрицы (A):
для оператора вращения как отношение собственных значений матрицы (A):

- Подготавливаем операторы поворота CR и отрицания CNOT с помощью пользовательских функций (код этих функций см. в контрольном примере ниже):

-
Расчет входного регистра
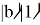 с помощью пользовательской функции:
с помощью пользовательской функции:

- Последовательное применение операторов квантовой схемы:

- Расчет результата и его вывод:

Контрольный пример программы для моделирования

Литература:
1. Смирнов Ю. А., Актимиров А. В. Моделирование квантового алгоритма Гровера для поиска схемотехнического решения в прикладной программе MATLAB // Молодой ученый. — 2019. — № 13. Часть 1 — С. 49–62.
- Нильсен М., Чанг И. Квантовые вычисления и квантовая информация. Пер. с англ. — М.: Мир, 2006. — 824 с.
- Hello quantum world! Google publishes landmark quantum supremacy claim // Nature. URL: https://www.nature.com/articles/d41586–019–03213-z (дата обращения: 10.12.2019).
- Quantum gold rush: the private funding pouring into quantum start-ups // Nature. URL: https://www.nature.com/articles/d41586–019–02935–4 (дата обращения: 10.12.2019).
- Europe shows first cards in €1-billion quantum bet // Nature. URL: https://www.nature.com/articles/d41586–018–07216–0 (дата обращения: 10.12.2019).
- Послание Президента Федеральному Собранию // Kremlin. URL: http://www.kremlin.ru/events/president/news/53379 (дата обращения: 10.12.2019).
- Росатом запускает масштабный проект по созданию отечественного квантового компьютера // Росатом. URL: https://www.rosatom.ru/journalist/news/rosatom-zapuskaet-masshtabnyy-proekt-po-sozdaniyu-otechestvennogo-kvantovogo-kompyutera/?sphrase_id=1032547 (дата обращения: 10.12.2019).
- Секреты военного технополиса «ЭРА» в Анапе раскрыли общественникам // URL: https://era-tehnopolis.ru/news/mass-media/sekrety-voennogo-tekhnopolisa-era-v-anape-raskryli-obshchest/ (дата обращения: 10.12.2019).
- Aram W. Harrow, Avinatan Hassidim, Seth Lloyd. «Quantum algorithm for linear systems of equations» // URL: https://arxiv.org/pdf/0811.3171 (дата обращения 14.12.2019).







