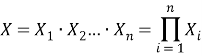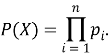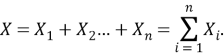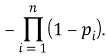При реализации проектов всегда присутствуют сведения, нарушение целостности или неправомочный доступ к которым могут привести к неблагоприятным последствиям, таким, например, как срыв проекта, судебный процесс, санкции со стороны заказчика и т. д. Очевидно, что далеко не каждая угроза актуальна для каждого из объектов информационной системы.
Чтобы выявить, рассмотреть и учесть возможные угрозы безопасности, для системы необходимо разработать модели угроз безопасности. Поскольку математический аппарат теории графов [1–3] позволяет однозначно описать структуру модели проекта, угрозы, воздействующие на уязвимости на отдельных этапах, для построения модели безопасности проекта будет применяться математический аппарат теории графов.
Ключевые слова: модель, безопасность, угроза, уязвимость, теория графов.
In the course of the activities of various organizations, projects are carried out. When implementing projects, there is always information, violation of integrity or unauthorized access to which can lead to adverse consequences, such as disruption of the project, litigation, sanctions by the customer, etc. Obviously, not every threat is relevant for each of the objects in the system.
In order to identify, consider and consider possible security threats, it is necessary for the system to develop models of security threats. Since the mathematical theory of graphs [1–3] allows us to unambiguously describe the structure of the project model, the threats that affect vulnerabilities at certain stages, the mathematical apparatus of graph theory will be used to build the project security model.
Основной целью данной работы является построение и анализ модели угроз и уязвимостей безопасности проекта для выявления наиболее существенных и требующих устранения угроз в зависимости от структуры угроз.
Для достижения поставленной цели необходимо разработать принцип построения модели угрозы информационной безопасности.
В ходе выполнения проектов можно столкнуться с различными комбинациями угроз безопасности, причём некоторые события (угрозы) могут не зависеть друг от друга или, напротив, наступать вследствие выполнения одного из них, могут происходить в один момент времени и т. д. Таким образом при построении модели безопасности для каждого конкретного проекта необходимо иметь представление о возможных угрозах, уметь оценивать их влияние на безопасность проекта, установить известные взаимосвязи угроз.
Для формирования последовательности угроз при выполнении проекта, можно воспользоваться представлением цепи или сети событий для обозначения цепочек угроз во время выполнения определённых этапов проектов [6].
Обозначим через A, B, C, … состояния системы до/после выполнения некоторой угрозы и выберем их как вершины графа. Тогда ребра этого графа представляют собой угрозы, реализация которых приводит к некоторому состоянию системы. Если реализация общей угрозы — события Х = (нарушение защищенности системы) требует прохождения нескольких этапов (состояний), то такая последовательность угроз представима в виде последовательной цепи (сети) событий
. Для обозначения факта выполнения или невыполнения угрозы воспользуемся бинарной кодировкой, где значение 0 будет означать что угроза не реализовалась, 1 — угроза реализовалась. Вероятность выполнения угрозы 
обозначим 
, вероятность нарушения защищенности системы (далее ВНЗС) обозначим P(X).
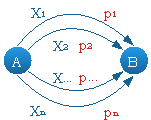
Угрозы, которые могут реализоваться одновременно и приводить к одному и тому же состоянию системы, можно представить в виде параллельной сети. В таблице 1 представлены формулы сети и вычисления вероятности для заданной структуры в общем виде для структуры из n элементов.
Таблица 1
Формулы сети ивычисления вероятности для заданной структуры
|
Схема |
Формула сети |
Формула вероятности |
|
Последовательная структура сети из n элементов |
||
|
|
|
|
|
Параллельная структура сети из n элементов |
||
|
|
|
|
Поскольку цепочка угроз может реализоваться через разные уязвимости системы, то приходим к более сложной структуре системы — «смешанной», состоящей как из последовательных, так и из параллельных участков сети (Рисунок 1). Структура отдельных частей данной сети не меняется, т. е. формула сети и вероятности сети, вычисляется согласно Таблице 1. Очевидно, что при усложнении структуры сети событий получаемые формулы будут весьма громоздкими.
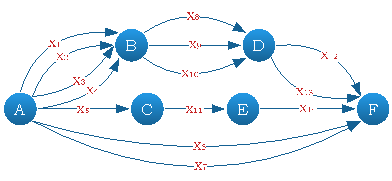
Рис. 1. Система, со смешанной структурой сети
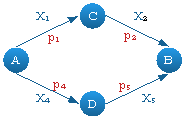
На пути каждой угрозы могут возникать ситуации, когда достижение одного состояния системы может быть осуществлено разными способами. Структуру такой системы обозначим как «мостовую». Схема элементарной мостовой структуры представлена на рисунке 2.
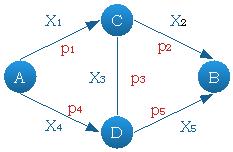
Рис. 2. Схема мостовой структуры
Вероятность реализации события АВ = (Угроза от состояния А до состояния В реализована, т. е. НЗС) для мостовой схемы рассчитывается по формуле полной вероятности:
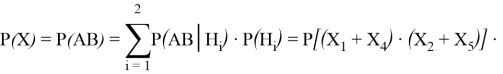
где Н1 и Н2 — гипотезы, согласно которым: Н1=(Угроза Х3 реализована) и Н2 = (Угроза Х3 не реализована).
Структура, схема и формулы сети при реализации (невыполнении) угрозы Х3 представлены в таблице 2.
Таблица 2
Структура, схема иформула сети при выполнении/не выполнении мостовой угрозы
|
Схема |
Формула сети |
Гипотеза |
|
|
|
|
|
|
|
|
— угроза 
— угроза 
Формула для вычисления вероятности реализации угрозы АВ:
Для вычислений используем известные формулы теории вероятностей для сложных событий.
Формула сложения вероятности (для суммы событий):
Формула умножения вероятности (для произведения независимых событий):
Их последовательное применение приводит к следующему выражению:
Так как часть угроз может выполняться или не выполняться, реализация некоторых цепочек угроз зависит от выполнения угроз на предшествующих этапах проекта.
Полученное выражение вычисления ВНЗС позволяет выявить самые слабые участки сети, т. е., определить не выполнение какой из угроз позволит обеспечить сохранность системы ввиду не выполнения целой цепочки угроз.
Выясним влияние каждой из угроз (её значимость) на вероятность реализации общей угрозы. Для этого необходимо в формуле вероятности сети найти частные производные по каждой переменной. Элемент с наибольшим её значением и должен стать объектом дальнейшего анализа.
После этого можно принять меры, чтобы данная угроза не реализовалась, что уменьшит вероятность нарушения безопасности системы.
При последовательной структуре системы, для вычисления частной производной по каждой из угроз необходимо воспользоваться следующей формулой:
(1)
Согласно данной формуле можно сделать вывод, что при последовательной структуре системы, лучше принимать меры, чтобы не реализовалась угроза, у которой будет наименьшее значение 
, т. е. нейтрализовать наименее вероятную угрозу в сети, что повлечет за собой не выполнение цепочки угроз.
При параллельной структуре системы, для вычисления частной производной по каждой из угроз необходимо воспользоваться следующей формулой:
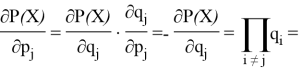
(2)
Согласно данной формуле можно сделать вывод, что при параллельной структуре системы, лучше принимать меры, чтобы не реализовалась угроза, у которой будет наибольшее значение , т. е. снизить вероятность выполнения или вовсе ликвидировать наиболее вероятную угрозу.
Рассмотрим пример 2 угроз для параллельной и последовательной структуры сети. Схемы сети аналогичны схемам в таблице 1.
Зададим вероятности выполнения угрозы случайным образом значениями от 0 до 1. Например, так:
Для последовательной структуры сети частные производные будут равны:
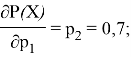
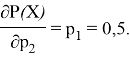
Из полученных результатов можно сделать вывод, что лучше попробовать избежать первой угрозы, т. е. необходимо уменьшать вероятность реализации наименее вероятной угрозы (формула 1).
Для параллельной структуры сети частные производные будут равны:
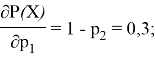
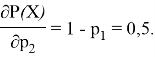
Из полученных результатов, можно сделать вывод, что лучше уменьшить вероятность выполнения второй угрозы, т. е., необходимо уменьшать вероятность реализации наиболее вероятной угрозы (формула 2).
Однако наибольший интерес для нас представляет «мостовая» угроза 
. Для начала найдём частные производные в общем виде:
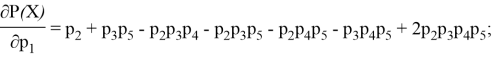
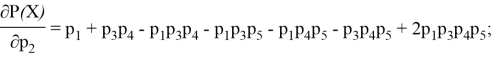
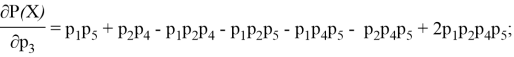
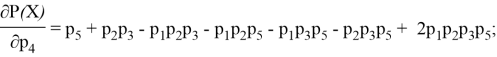
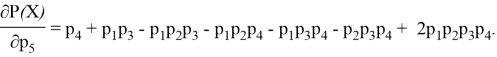
После проведения ряда экспериментов (наименьшее/наибольшее значение вероятности выполнения мостовой угрозы) были получены разные результаты, из чего следует вывод, что нельзя определить однозначную закономерность, для выявления наиболее значимой угрозы необходимо рассматривать конкретные, интересующие случаи. В данной статье были рассмотрены основные типы структур сети, определены базовые формулы, при помощи которых можно определить основные закономерности, например, при последовательной структуре сети лучше избегать реализации наименьшей угрозы, а при параллельной напротив — наиболее вероятной. Для анализа более сложных структур (мостовой, смешанной) необходимо построение имитационную модель, вывод формул, позволяющих на основе входных данных в виде угроз разного вида и типа и их характеристик, рассчитать распределение угроз, а также получить статистические характеристики для дальнейшего анализа.
Литература:
- С. Цой, С. М. Цхай. Прикладная теория графов. — Алма-Ата: Наука, 1971, 499 с.
- Сигорский В. П. Математический аппарат инженера. — Киев: Техника, 1975,765 с.
- Белов В. В., Воробьев Е. М., Шабалов В. Е. Теория графов. — М.: Высшая школа, 1976, 396 с.
- Феллер В. Введение в теорию вероятностей и её приложения. В 2-х томах. — М.: Мир, 1984. — Т. 1: 528 с., Т. 2: 738 с.
- Карлин С. Основы теории случайных процессов. — М.: Мир, 1971. — 536 с. 8.
- Нуммелин Э. Общие неприводимые цепи Маркова и неотрицательные операторы. — М.: Мир, 1989. — 207 с.
