Орнаменты на плоскости

Данная статья посвящена изучению математических законов и принципов построения орнаментов, а также разработке алгоритмов и программного обеспечения по созданию орнаментов и апробированию их на практике.

Орнамент (от латинского ornamentum – украшение) – узор, состоящий из ритмически упорядоченных элементов, для украшения каких-либо предметов или архитектурных сооружений. Известный во всем мире математик Г. Вейль назвал орнаментальное искусство «самым древним видом высшей математики, выраженной в неявной форме»¹.

Актуальность темы состоит в постоянном расширении сфер применений орнаментального искусства в современном мире (не только в геометрии, но и в архитектуре, живописи, химии, физике, технике и др.), глубокой связи его с историей развития человечества.

Задачи исследования: проанализировать специальную литературу и теоретически обосновать существование 17 различных видов орнаментов; выбрать некоторые аспекты методики построения орнаментов; проверить выбранные приемы в опытно-экспериментальной работе через разработку программного обеспечения.

Гипотеза: если изучить приемы построения орнаментов, то повысится эффективность усвоения геометрического материала, мотивация изучения геометрии, качество выполнения чертежей, более явственной станет связь между геометрией и реальной жизнью, а также межпредметная связь.

База исследования: свойства симметрии, симметричные фигуры.

При описании симметрии фигур следует опираться на два утверждения:

1). Если движение является преобразованием симметрии фигуры, то обратное ему движение также есть преобразование симметрии данной фигуры.

2). Если два движения являются преобразованиями симметрии фигуры, то их композиция также является преобразованием симметрии данной фигуры².

Симметрия – один из видов гармонической композиции. Она служит основным приемом для построения бордюров и орнаментов плоских фигур, обладающих соответственно одной или несколькими симметриями переноса в сочетании с зеркальными отражениями.

В тех случаях, когда некоторая совокупность преобразований обладает указанными свойствами, говорят, что эта совокупность является группой преобразований фигуры. В частности, когда преобразованиями фигуры являются все ее преобразования симметрии, говорят о группе симметрии фигуры.

Методологическая основа исследования: изучение приемов построения орнаментов с учетом типа квадратной плоской точечной решетки, являющейся основой любого орнамента. Если отметим на плоскости четыре вершины квадрата, площадь которого равна единице, затем сдвинем квадрат по всем направлениям на длину, равную стороне квадрата, и отметим вновь получившиеся вершины, то получим решетку. В ней можно образовать из четырех точек также и другие фигуры, не только квадраты (например, параллелограммы). Они называются элементарными ячейками или фундаментальной областью решетки. Точки называют узлами решетки. Тип плоской решетки определяет характер переносной симметрии данного орнамента. Всего при создании плоских орнаментов используется пять типов решеток: квадратная, прямоугольная, гексагональная, ромбическая, косая.

Т.к. каждая фигура строится по характеристическим точкам, то в основу построения орнаментов положена плоская точечная система. Определим понятие правильной точечной системы следующим образом:

1) такая система должна содержать бесконечное множество точек, причем, число точек, лежащих внутри круга должно возрастать пропорционально квадрату радиуса до бесконечности;

2) содержит во всякой конечной области лишь конечное число точек;

3) имеет одинаковое расположение по отношению к любой из своих точек или всякая точка правильной точечной системы может быть переведена в другую точку системы путем совмещения.³

Получается орнамент следующим образом: наносится узор в элементарной ячейке (или ее части), и эта ячейка подвергается преобразованиям, допустимым для нее (то есть, чтобы решетка переходила в себя). Таким образом, плоскость заполняется равными областями, и на ней задается узор.

В принципе, любой орнамент можно построить посредством параллельных переносов заполненной определенным рисунком элементарной ячейки. Такой способ построения орнамента является единственным в том случае, когда орнамент не обладает ни зеркальной, ни поворотной симметрией. В остальных случаях возможны иные способы построения орнамента; при этом в качестве исходного изображения (основного мотива) используют не всю элементарную ячейку орнамента, а лишь часть ее.

Теоретическая основа исследования: изучение дискретных групп движений, приводящих к правильным точечным системам (федоровских групп движений). Изучаемая теория принадлежит Е.С.Федорову, русскому кристаллографу и геометру. В 1885-1890 годах он выполнил серию работ по структуре и симметрии кристаллов, завершившуюся классическим трудом «Симметрия правильных систем фигур». В нем приведен вывод 230 пространственных групп (федоровских групп). Все эти группы имеют конечные фундаментальные области. При рассмотрении групп мы снова имеем дело с плоскими точечными решетками⁴. Этот труд позволяет доказать, что всего существует 17 типов орнаментов, а также доказать существование только пяти возможных федоровских групп движений на плоскости.

Результатом изучения орнаментов являются построенные по алгоритму и созданным программам некоторые орнаменты.

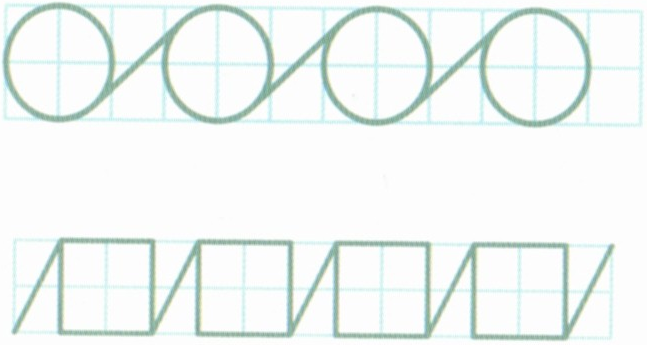
1. Прямоугольный орнамент.

Общий порядок построения орнамента:

1. Нарисовать базовые квадраты;

2. Начертить прямоугольники на основании квадратов и/или добавить вспомогательные линии;

3. Повторить мотив;

4. Окантовать орнамент по краю.

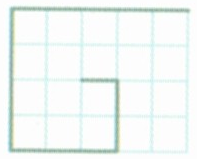
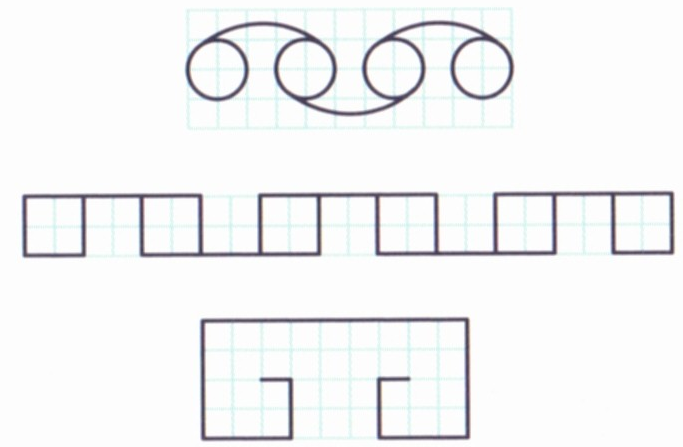
Существует три способа построения прямоугольных орнаментов:

1. Создание смежных квадратов;

2. Определение точек выхода;

3. Выполнение и поворачивание узора.

1. Прямоугольные орнаменты получаются при преобразовании квадратов из кругов с двумя точками выхода:

Рисунок 1

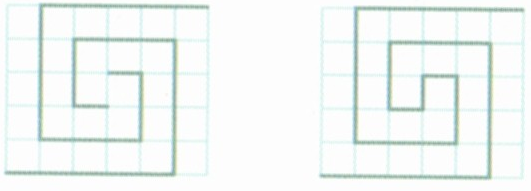
Открытый квадрат позволяет присоединить смежный, а центры переплетающихся квадратов можно оставить открытыми или закрыть дополнительной линией:

Рисунок 2

Соединение мотивов с помощью вертикальных линий и добавление окантовки вверху и внизу бордюра для образования двойной полосы:

Рисунок 3

Окрашенные полосы придают орнаменту большую декоративность:

Рисунок 4

2. Аналогично можно создать орнамент на основе еще одного базового элемента:

Рисунок 5

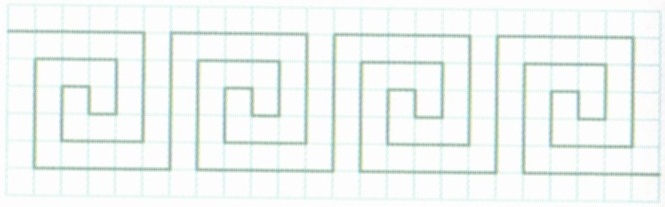
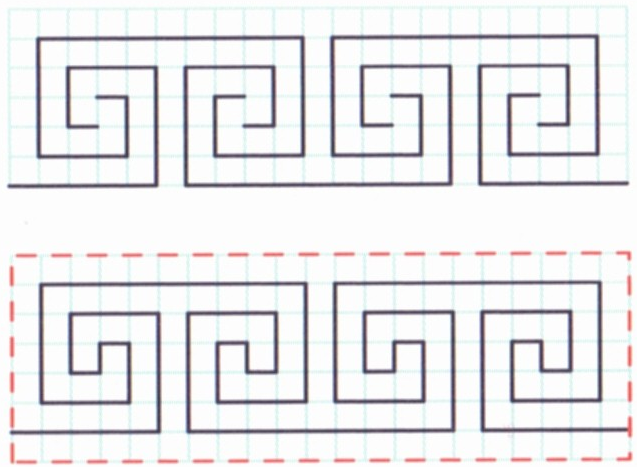
В результате применения алгоритма, описанного выше, получен бордюр из повторяющихся мотивов:

Рисунок 6

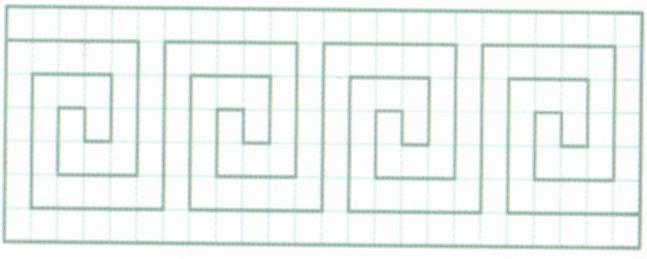
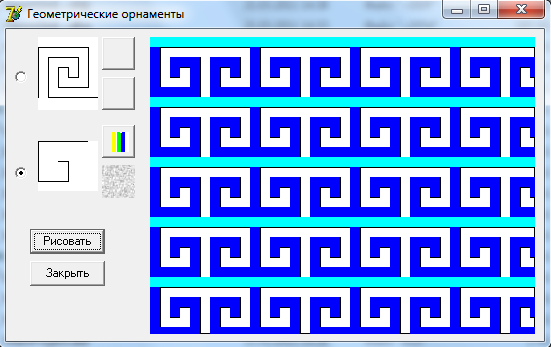
Полученный орнамент имеет вид:

Рисунок 7

2. Треугольник Серпинского.

Рассмотрим фрактал, один из двумерных аналогов множества Кантора предложенный польским математиком Серпинским в 1915 году. Также известен, как «решётка» или «салфетка» Серпинского. Общий порядок построения:

1. Равносторонний треугольник M₀ делится прямыми, параллельными его сторонам, на 4 равных равносторонних треугольника;

2. Из треугольника удаляется центральный треугольник. Получается множество M₁, состоящее из 3 оставшихся треугольников "первого ранга";

3. Поступая точно так же с каждым из треугольников первого ранга, получим множество M₂, состоящее из 9 равносторонних треугольников второго ранга. Продолжая этот процесс бесконечно, получим бесконечную последовательность:

пересечение членов которой есть треугольник Серпинского.

Рисунок 8

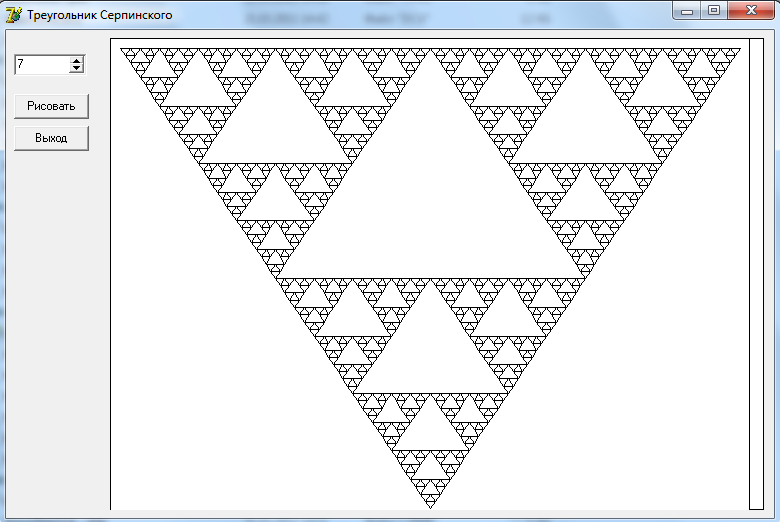
Полученный орнамент имеет вид:

Рисунок 9

Описанный орнамент можно построить с помощью программирования. В приложении находится исходный код программы.

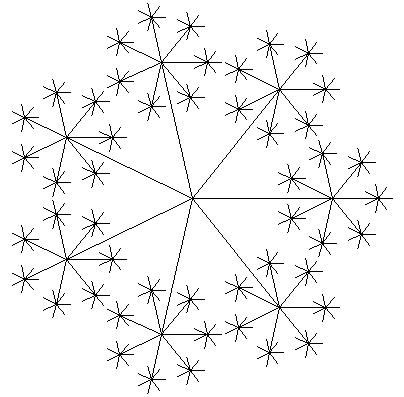
3. Снежинка.

Форма снежинок может быть очень разнообразной, но все они обладают симметрией – поворотной симметрией и, кроме того, зеркальной симметрией.

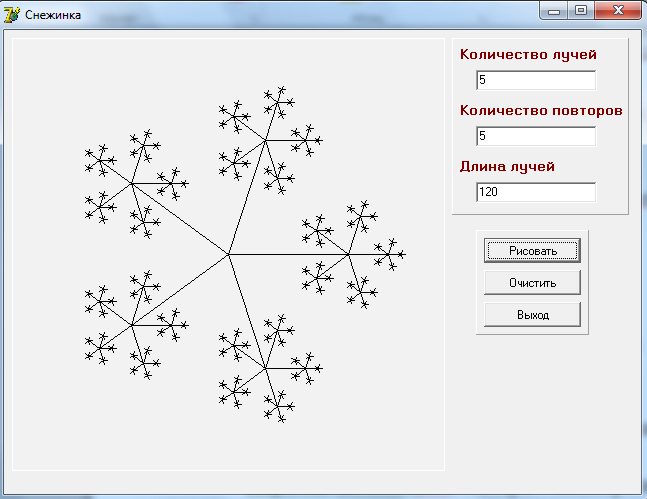
Общий порядок построения:

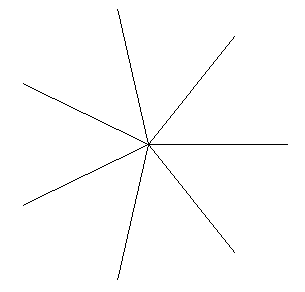
1. Построить выбранное количество отрезков с общим началом;

2. На конце каждого отрезка построить то же самое количество отрезков, длина которых равна 1/3 длины исходного отрезка;

3. Повторить это действие заданное число раз.

Рисунок 10

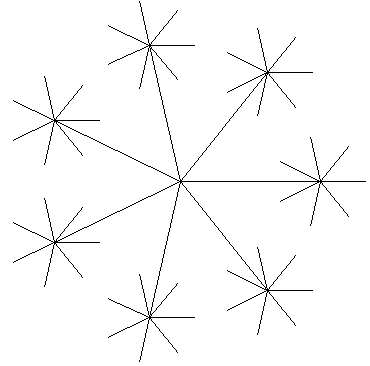
Полученный орнамент имеет вид:

Рисунок 11

Описанный орнамент можно построить с помощью программирования. В приложении находится исходный код программы.

4. Орнаменты на основе изображения.

1. Орнаменты с использованием параллельного переноса.

Общий порядок построения:

1. Поместить изображение в элементарную ячейку;

2. Используя параллельные переносы, повторить изображение многократно.

Рисунок 12

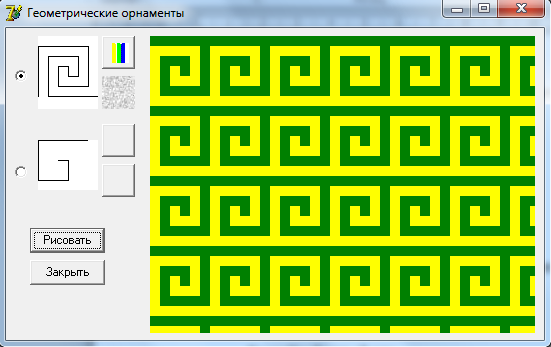
Полученный орнамент имеет вид:

Рисунок 13

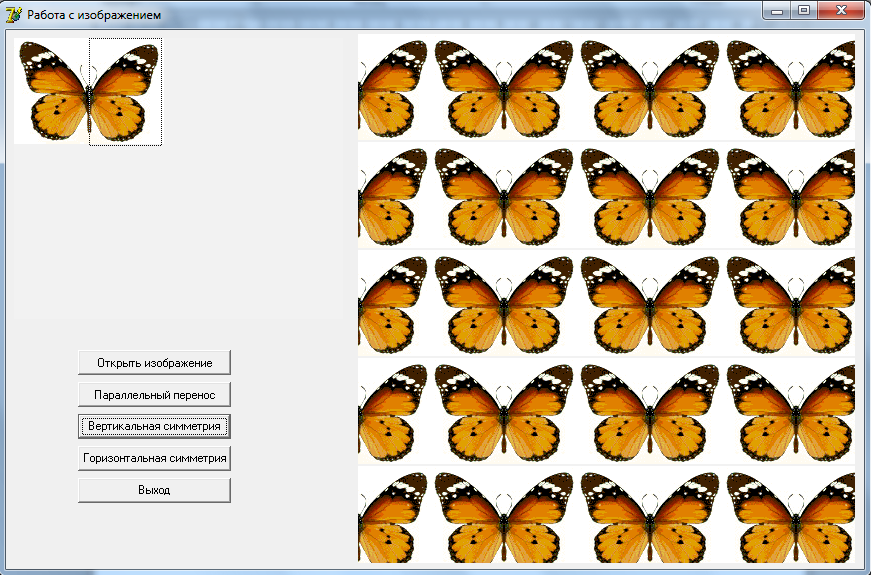
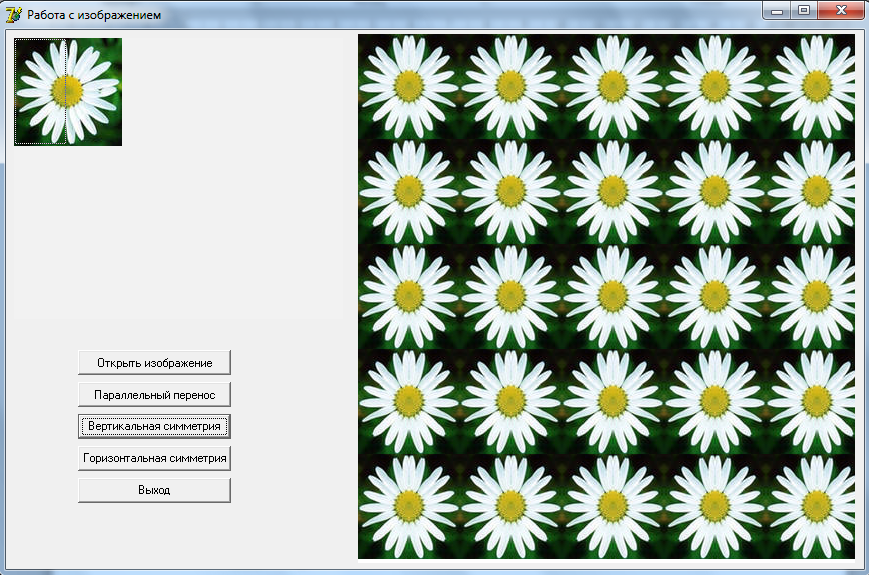
2. Орнамент с использованием параллельного переноса и осевой симметрии с вертикальной осью симметрии.

Общий порядок построения:

1. Поместить изображение в элементарную ячейку;

2. С помощью осевой симметрии с вертикальной осью симметрии отразить изображение;

3. Используя параллельные переносы, повторить полученное изображение многократно.

Рисунок 14

Полученный орнамент имеет вид:

Рисунок 15

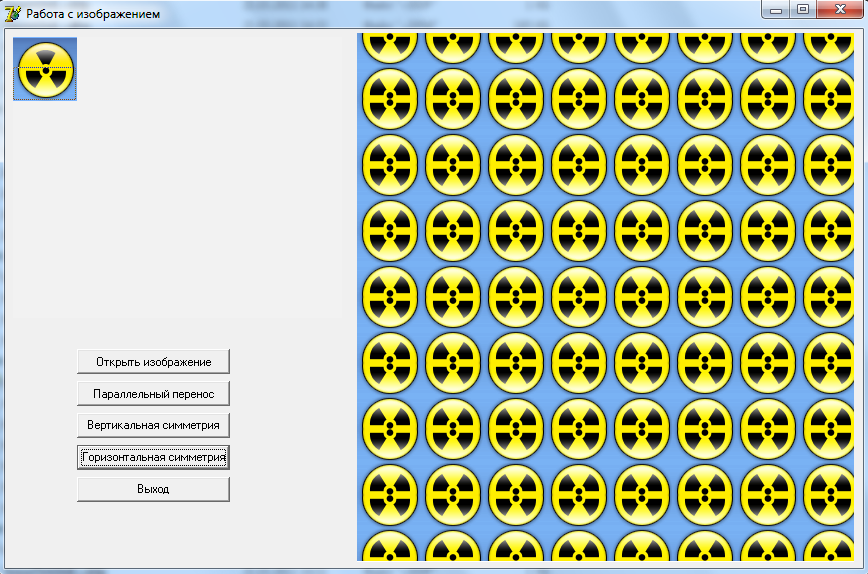
3. Орнамент с использованием параллельного переноса и осевой симметрии с горизонтальной осью симметрии.

Общий порядок построения:

1. Поместить изображение в элементарную ячейку;

2. С помощью осевой симметрии с горизонтальной осью симметрии отразить изображение;

3. Используя параллельные переносы, повторить полученное изображение многократно.

Рисунок 16

Полученный орнамент имеет вид:

Рисунок 17

В данной работе мне хотелось доказать еще раз непосредственную связь геометрии с практической жизнью. Ведь любые теоретические открытия направлены, в конечном итоге, на дальнейшее практическое применение, а иначе, зачем они совершаются?

Способы построения орнаментов с использованием свойств различных видов движения становятся понятными благодаря изучению федоровских групп движения, правильных точечных групп движений, т.е. точечных решеток. Так восхождение от простого к сложному дает возможность обосновать правила построения фигур, обладающих свойствами симметрии.

Литература:

1. Вейль Г. Симметрия - М.: Наука, 1968.
2. Александров А.Д., Вернер А. Л.. Геометрия 8-9 - М.: Просвещение, 1991.
3. Гильберт Д., Кон-Фоссен С. Перевод Александрова П.С. Наглядная геометрия -М.: Просвещение, 1962.
4. Ред. Прохоров Ю.В. Математический энциклопедический словарь - М.: Советская энциклопедия, 1988.