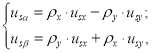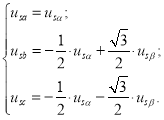Моделирование преобразователей координат и АИН ШИМ в Си



Моделирование преобразователей координат и АИН ШИМ в Си

Емельянов Александр Александрович, старший преподаватель;

Бесклеткин Виктор Викторович, старший преподаватель;

Агзамов Игорь Маратович, студент;

Зозулин Михаил Сергеевич, студент;

Зорин Дмитрий Иванович, студент;

Бухряков Иван Федорович, студент;

Онищенко Константин Юрьевич, студент;

Дятлов Олег Алексеевич, студент

Российский государственный профессионально-педагогический университет (г. Екатеринбург)

Пестеров Дмитрий Ильич, студент магистратуры

Уральский государственный университет путей сообщения (г. Екатеринбург)

В работе [1] приведена функциональная схема математической модели САР скорости системы «АИН ШИМ – АД». Моделирование проводилось в Matlab-Script. В данной статье приводим небольшую часть этой схемы, состоящую из преобразователей координат и автономного инвертора напряжения с широтно-импульсной модуляцией (АИН ШИМ), как показано на рис. 1.

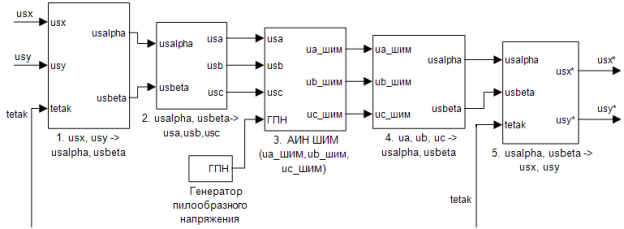
Рис. 1. Преобразователи координат и АИН ШИМ

Цель данной работы – создание программы этой подсистемы на языке Си.

С помощью первого элемента производится преобразование вектора с проекциями u_sx и u_sy из системы координат, вращающейся с частотой ω_к, в неподвижную декартову систему координат с осями α и β, в которой в каждый момент времени будут определяться по следующим зависимостям [2], [3]:

(1)

гдеρ_x = cos θ_к и ρ_y = sin θ_к.

Угол поворота θ_к определяется из следующей формулы:

(2)

Производная dθ_к в работе [1] была представлена через конечные разности:

Отсюда:

(3)

При программировании в Си из всех уравнений исключаем скобки (i) и (i+1). В этом случае уменьшается число символов и, если число циклов составляет сотни тысяч, то это скажется на быстродействии расчета. Рассмотренные выше уравнения в этом случае примут следующий вид:

Примечания:

1. Скорость вращения координатной системы ω_к вычисляется в системе [1] в блоке «наблюдатель».

При программировании в Си подсистемы (рис. 1) примем в формуле ω_к = 2π·f частоту f = 50 Гц = const.

Для того, чтобы использовать число π = 3,14…, необходимо ввести заголовочный файл #include __STRICT_ANSI__. Число π в Си обозначается M_PI, тогда скорость вращения ω_к запишется в следующем виде:

2. Проекции статорного напряжения u_sx и u_sy в работе [1] вычисляются на выходе регуляторов тока по проекциям x и y с учетом алгебраической суммы сигналов с выхода звена компенсации перекрестных связей. В данной работе примем u_sx = 1 и u_sy = 0.

3. В начале программы идет перечисление переменных us_alfa, us_beta, t, tau и т.д. В каждом цикле стираются предыдущие значения этих переменных и записываются новые. Для того, чтобы увидеть графическое изображение изменения тех или иных переменных во времени, используется программа «gnuplot», которая состоит из более шестисот операторов. «Gnuplot» необходим либо в обучающих программах, либо на стадии отладки программ. После отладки «gnuplot» удаляют из программы и загружают в микроконтроллер только рабочую программу, а графики смотрят на реальном осциллографе.

На рис. 2 приведена программа реализации на языке Си первого блока преобразования координат. Зависимости us_alfa и us_beta во времени даны на рис. 3.

В следующем блоке осуществляется преобразование проекций вращающего вектора u_sα и u_sβ в мгновенные значения по проекциям вращающегося вектора на оси a, b, c неподвижной трехфазной системы координат.

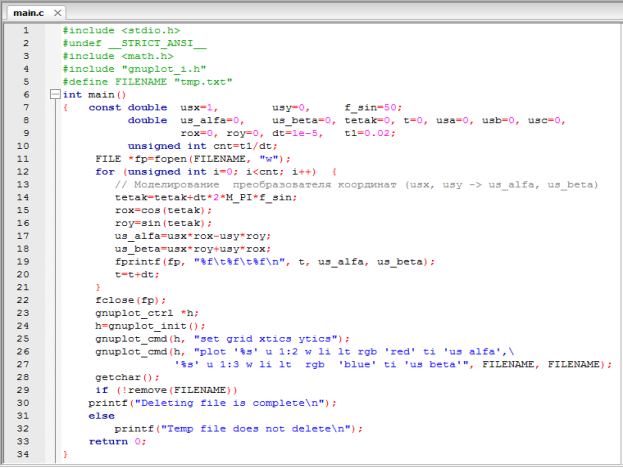
Рис. 2. Программа преобразования вектора из вращающейся системы (x, y) координат в неподвижную декартову систему (α, β)

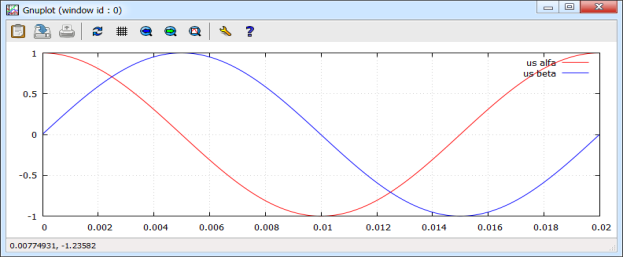
Рис. 3. Зависимости us_alfa и us_beta на выходе первого преобразователя

Формулы преобразования приведены в работах [2], [3] и имеют следующий вид:

(4)

Мгновенные значения u_sb и u_sc при программировании в Си лучше дать в следующем виде:

В Си система уравнений (4) будет иметь следующий вид:

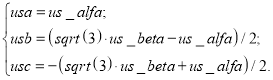
Полная программа двухэтапного обратного преобразования в Си приведена на рис. 4.

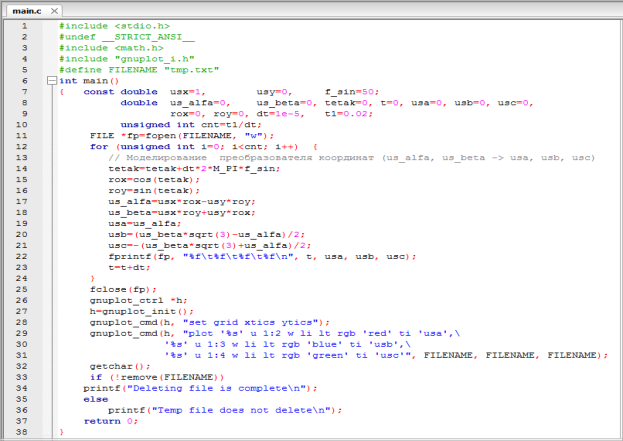
Рис. 4. Программа двухэтапного обратного преобразования вектора из вращающейся системы координат в неподвижную трехфазную систему

Результаты программирования u_sa, u_sb и u_sc приведены на рис. 5.

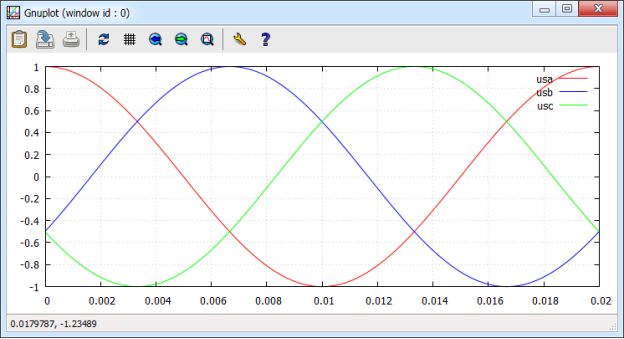
Рис. 5. Зависимости u_sa, u_sb и u_sc во времени

Сигналы usa, usb и usc с выхода второго блока подаются на следующий блок – автономный инвертор напряжения с широтно-импульсной модуляцией. Этот блок состоит из двух частей: нуль-орган и инвертор напряжения.

Для лучшего понимания приведем на рис. 6 моделирование нуль-органа в Matlab-Simulink и Matlab-Script из работы [1]. Достоинством моделей в Simulink является наглядность. Видимы связи сигналов, например, для фазы «a»: сигнал usa сравнивается с сигналом, поступающим с генератора пилообразного напряжения, и за сумматором устанавливается релейный элемент, чувствительный к знаку, и как бы ни менялись величины входных сигналов на сумматоре, он скачком поддерживает постоянный уровень сигнала. Как только меняются знаки на выходе сумматора, мгновенно релейный элемент скачком переключает на противоположный и поддерживает его постоянным и т.д. На выходе релейного элемента получаются ступенчатые сигналы с разной шириной по времени, отсюда название – широтно-импульсная модуляция. В левом нижнем углу показаны осциллограммы выходных сигналов нуль-органов по фазам f_a, f_b и f_c, получивших название «коммутационные функции».

В правой части показана программа с логическими операторами на универсальном языке математики. Ценность этой формы моделирования (программирования) в его универсальности.

Для того, чтобы перейти к программированию в Си, достаточно убрать (i) и (i+1). Чем меньше символов, тем выше скорость расчета.

На рис. 7 приведено программирование нуль-органа в Си для фазы «а». На рис. 8 показаны результаты моделирования по одной фазе, и мы увидим копию осциллограмм в Matlab и Си.

На рис. 9 приведены математические зависимости выходных напряжений АИН – usa_pwm, usb_pwm и usc_pwm от коммутационных функций fa, fb и fc [2], [3]. В левой верхней части приведена реализация этих формул на математической модели Matlab-Simulink, а в правой нижней части в Matlab-Script. В нижней левой части даны осциллограммы пятиуровневых выходных напряжений АИН ШИМ (, , , , ).

Ценность данного рисунка (рис. 9), приведенного из работы [1], состоит в том, что на одном листе представлены вместе формулы и различные способы реализации. Снова исключив из математической модели Matlab-Script (i) и (i+1), переходим к программе АИН ШИМ на языке Си.

На рис. 10 приведена полная программа, включающая не только АИН ШИМ, но и двухэтапные обратные преобразователи. Результаты моделирования на выходе блока 3 представлены на рис. 11.

На рис. 12 дана программа всех элементов подсистемы (АИН ШИМ – преобразователи координат) в Си. Результаты моделирования на выходе блоков 4 и 5 приведены на рис. 13 и 14.

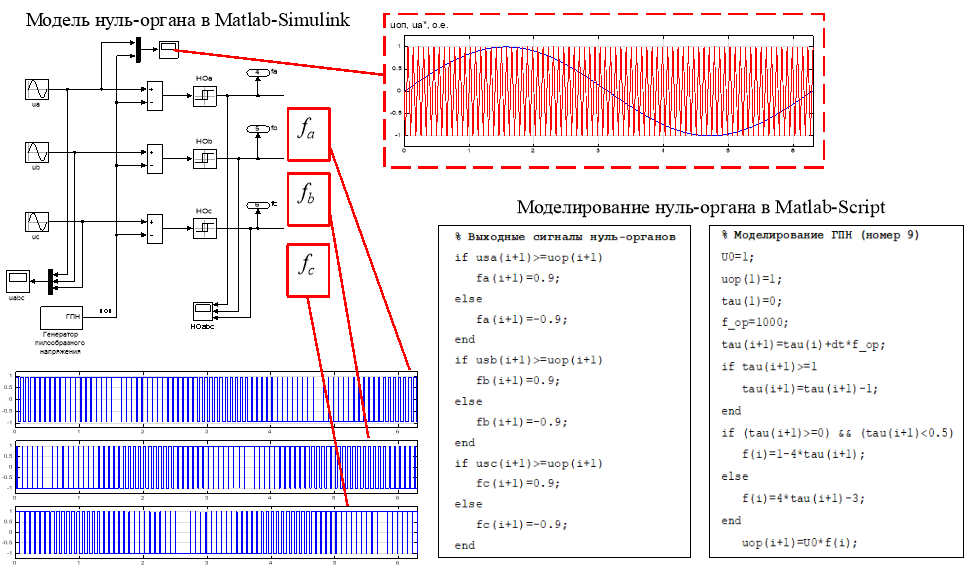
Рис. 6. Нуль-орган в Simulink и Matlab-Script

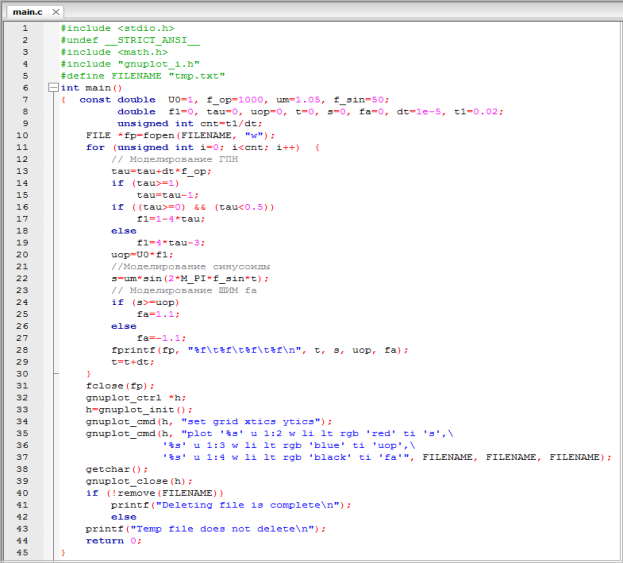
Рис. 7. Моделирование usa, uop и fa для фазы «а» в Си

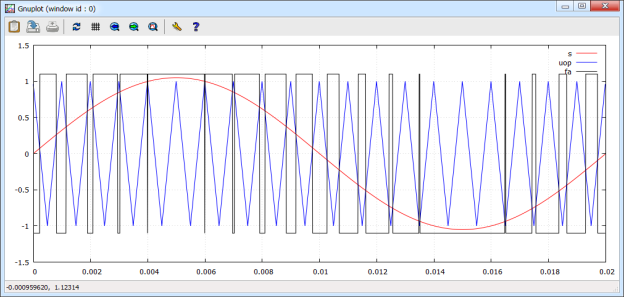
Рис. 8. Зависимости usa, uop и fa от времени

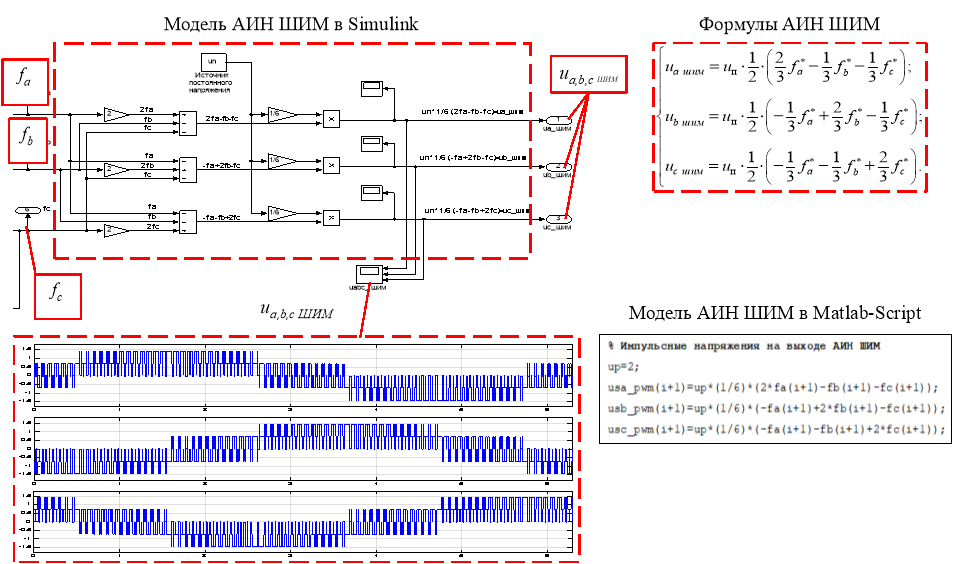
Рис. 9. Моделирование АИН ШИМ в Simulink и Matlab-Script

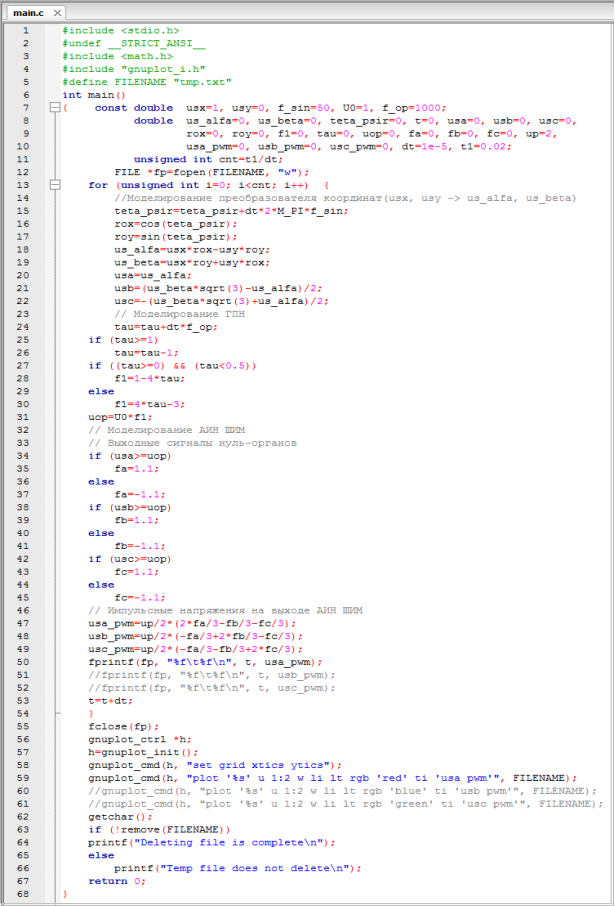
Рис. 10. Программирование в Си АИН ШИМ на выходе блока 3 с учетом двухэтапного обратного преобразования координат

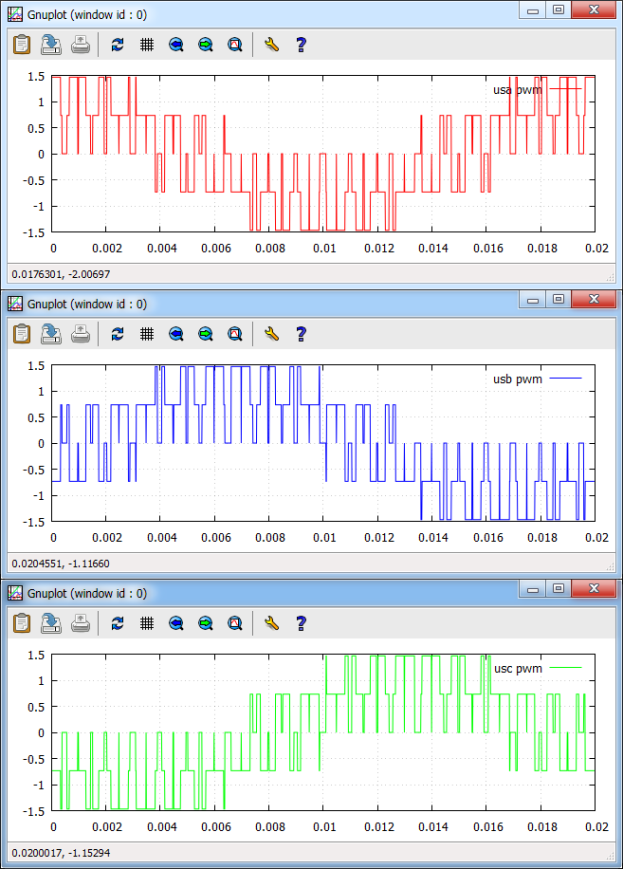
Рис. 11. Зависимости usa_pwm, usb_pwm и usc_pwm на выходе блока 3

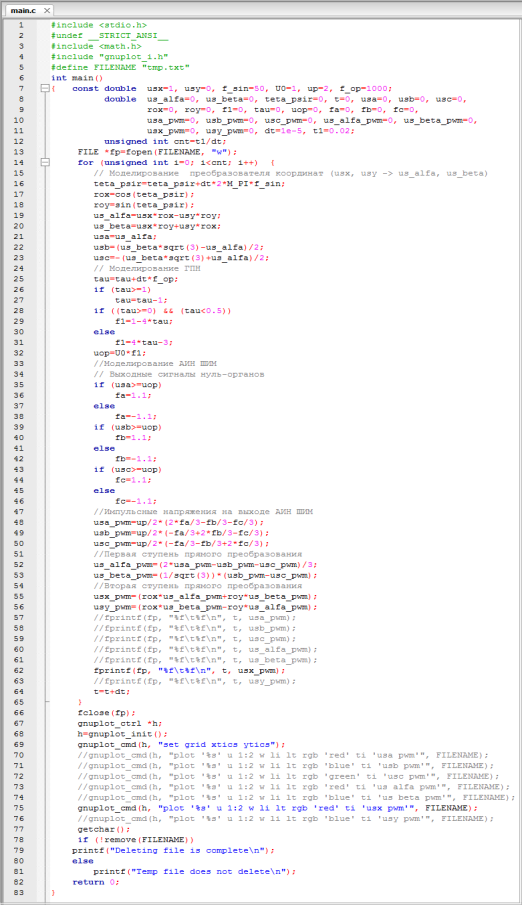
Рис. 12. Программирование в Си всех элементов подсистемы (АИН ШИМ – преобразователи координат)

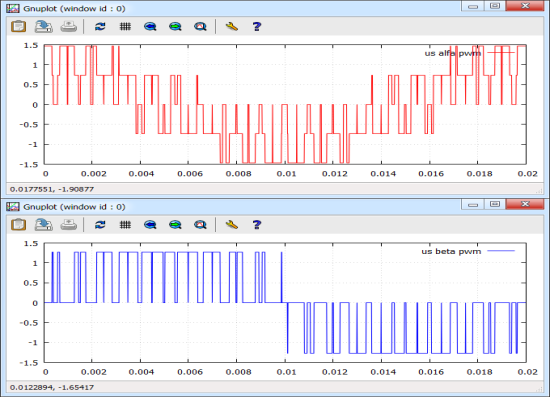
Рис. 13. Сигналы us_alfa_pwm и us_beta_pwm на выходе блока 4

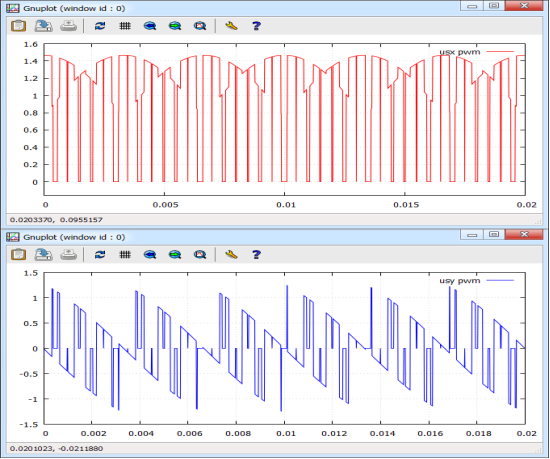
Рис. 14. Сигналы usx_pwm и usy_pwm на выходе блока 5

Литература:

1. Емельянов А.А., Гусев В.М., Пестеров Д.И., Даниленко Д.С., Воротилкин Е.А., Коновалов И.Д., Бесклеткин В.В., Иванин А.Ю. Моделирование САР скорости системы «АИН ШИМ – АД» с переменными ψr - is в Matlab-Script в системе относительных единиц // Молодой ученый. — 2018. — №22. — С. 6-31.
2. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. - Екатеринбург: УРО РАН, 2000. - 654 с.
3. Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.
4. Васильев А.Н. Программирование на C++ в примерах и задачах. – М.: Издательство «Э», 2017. – 368 с.