Данная работа является модификацией работы [1], в которой модель асинхронного двигателя (АД) была представлена в виде системы, состоящей из оболочки двигателя (рис. 1) и подсистем с расчетом параметров в Simulink.
В этой работе расчет параметров производится в Script. Для лучшего понимания предварительно необходимо рассмотреть работы [2], …, [6], в которых подробно получены математические уравнения асинхронного двигателя.
В главе 6 «Примеры» [7] дан образец расчета параметров асинхронного двигателя. Для цельности изложения вначале приведем этот пример и далее представим программу расчета в Script.
Номинальные данные:
Номинальный режим работы S1;
Номинальная мощность 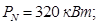
Номинальное фазное напряжение 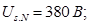
Номинальный фазный ток 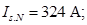
Номинальная частота 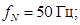
Номинальная синхронная скорость 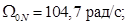
Номинальная скорость ротора 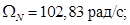
Номинальный КПД 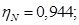
Номинальный коэффициент мощности 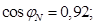
Число пар полюсов 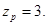
Параметры Т-образной схемы замещения при номинальной частоте:
Активное сопротивление обмотки статора 
Индуктивное сопротивление рассеяния обмотки статора 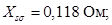

Рис. 1. Оболочка асинхронного двигателя с переменными 
Активное сопротивление обмотки ротора, приведенное к статору 
Индуктивное сопротивление рассеяния обмотки ротора, приведенное статору 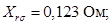
Главное индуктивное сопротивление 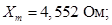
Суммарный момент инерции двигателя и механизма 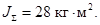
Базисные величины системы относительных единиц:
Напряжение 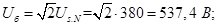
Ток 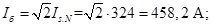
Частота 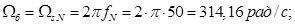
Скорость ротора 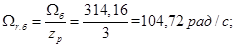
Сопротивление 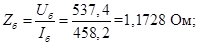
Потокосцепление 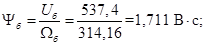
Индуктивность 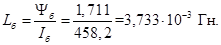
Используя номинальные данные двигателя, определяем:
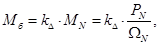
где 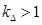 – коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (
– коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (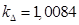 ).
).
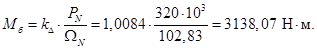
В качестве базисной мощности выбираем значение электромагнитной мощности двигателя в номинальном режиме, определяемое по следующей формуле:
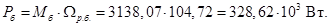
Относительные значения параметров схемы замещения двигателя:
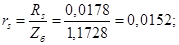
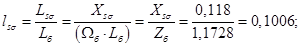
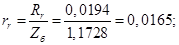
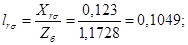
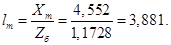
Механическая постоянная времени:
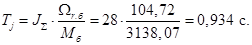
Номинальное значение скольжения:
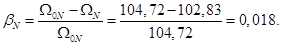
Относительное значение номинальной скорости ротора:
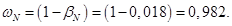
Нормирующий энергетический коэффициент:
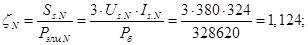
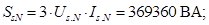
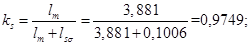
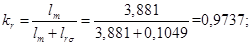
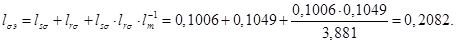
При расчете режимов работы, для того чтобы 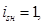
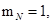
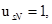
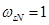 и
и 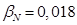 необходимо откорректировать
необходимо откорректировать 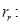
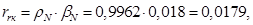
где 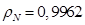 – корректирующий коэффициент [7, с. 296].
– корректирующий коэффициент [7, с. 296].
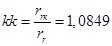 - коэффициент, показывающий отношение
- коэффициент, показывающий отношение 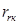 к
к 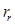 .
.
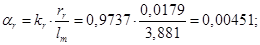
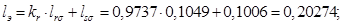
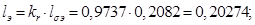
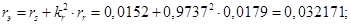
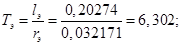
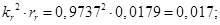
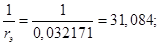
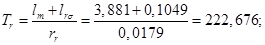
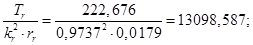
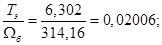
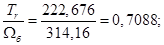
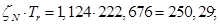
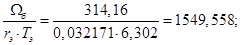
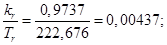
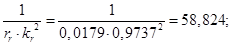
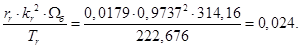
Расчет этих коэффициентов производим в Script:
%Номинальные данные
PN=320000;
UsN=380;
IsN=324;
fN=50;
Omega0N=104.7;
OmegaN=102.83;
nN=0.944;
cos_phiN=0.92;
zp=3;
%Параметры Т-образной схемы замещения при номинальной частоте
Rs=0.0178;
Xs=0.118;
Rr=0.0194;
Xr=0.123;
Xm=4.552;
J=28;
%Базисные величины системы относительных единиц
Ub=sqrt(2)*UsN;
Ib=sqrt(2)*IsN;
OmegasN=2*pi*fN;
Omegab=OmegasN;
Omegarb=Omegab/zp;
Zb=Ub/Ib;
Psib=Ub/Omegab;
Lb=Psib/Ib;
kd=1.0084;
Mb=kd*PN/OmegaN;
Pb=Mb*Omegarb;
rs=Rs/Zb;
ls=Xs/Zb;
rr=Rr/Zb;
lr=Xr/Zb;
lm=Xm/Zb;
Tj=J*Omegarb/Mb;
betaN=(Omega0N-OmegaN)/Omega0N;
wN=(1-betaN);
SsN=3*UsN*IsN;
zetaN=SsN/Pb;
ks=lm/(lm+ls);
kr=lm/(lm+lr);
lbe=ls+lr+ls*lr*lm^(-1);
roN=0.9962;
rrk=roN*betaN;
alphar=kr*rr/lm;
le=kr*lbe;
re=rs+(kr^2)*rr;
Te=le/re;
Tr=(lm+lr)/rr;
wk=1;
Us=1;
ws=1;
t=2;
%Преобразователь координат и блок ориентации
gamma=1.4168*pi*1.47;
usa=Us*cos(ws*t);
usb=Us*cos(ws*t-2*pi/3);
usc=Us*cos(ws*t+2*pi/3);
us_alpha=(1/3)*(2*usa-usb-usc);
us_beta=1/(sqrt(3))*(usb-usc);
rox=cos(gamma);
roy=sin(gamma);
usx=rox*us_alpha+roy*us_beta;
usy=-roy*us_alpha+rox*us_beta;
%Значения параметров для Simulink
a1=Omegab/(re*Te);
a2=(kr^2)*rr*Omegab/Tr;
a3=1/(kr^2)/rr;
a4=Tr/(rr*(kr^2));
a5=zetaN*Tr;
a6=1/Tj;
На рис. 2 и 3 показаны связи расчетных коэффициентов в Script и внешние связи системы.

Рис. 2. Связь коэффициентов модели с коэффициентами в Script

Рис. 3. Внешние связи системы
Результаты исследований представлены на рис. 4, 5 и 6.
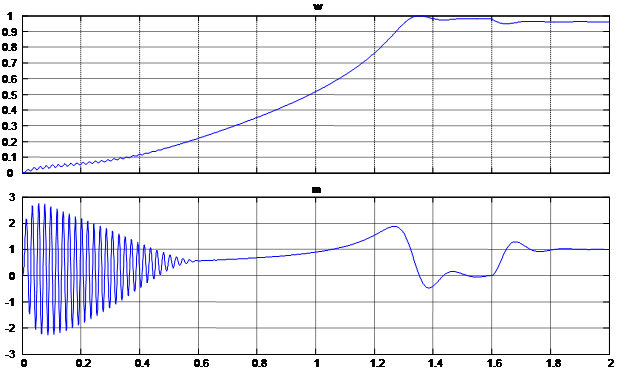
Рис. 4. Графики скорости и момента
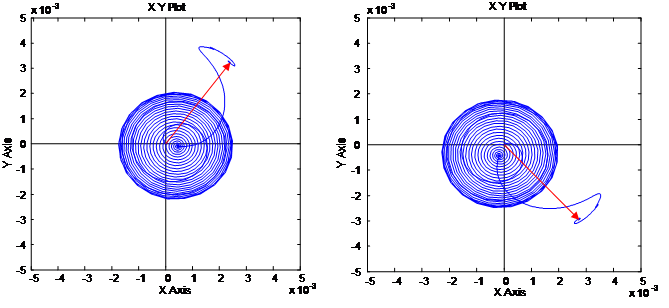
Рис. 5. Произвольная ориентация системы координат
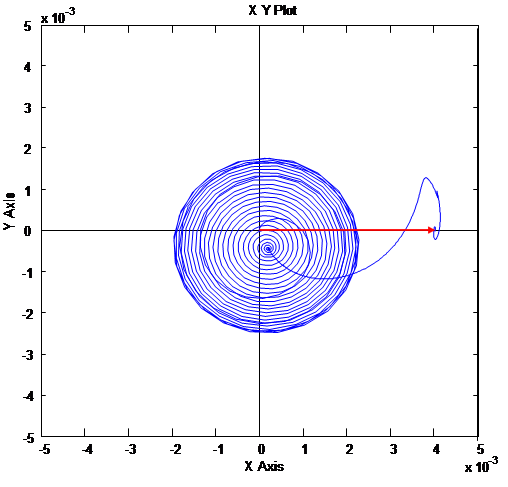
Рис. 6. Ориентация системы координат по потокосцеплению ротора
Литература:
1. Емельянов А.А., Бесклеткин В.В., Авдеев А.С., Чернов М.В., Киряков Г.А., Габзалилов Э.Ф., Фуртиков К.А., Реутов А.Я., Королёв О.А., Азанов А.А. Математическая модель асинхронного двигателя с переменными 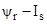 в произвольной системе координат в системе Script-Simulink // Молодой ученый. – 2015. - № 17.
в произвольной системе координат в системе Script-Simulink // Молодой ученый. – 2015. - № 17.
3. Емельянов А.А., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Чернов М.В., Киряков Г.А., Габзалилов Э.Ф., Фуртиков К.А., Реутов А.Я., Королёв О.А. Пространственные векторы в асинхронном двигателе в относительной системе единиц // Молодой ученый. - 2015. - № 11. - С. 133-156.
5. Емельянов А.А., Бесклеткин В.В., Авдеев А.С., Чернов М.В., Киряков Г.А., Габзалилов Э.Ф., Фуртиков К.А., Реутов А.Я., Королёв О.А. Математическая модель асинхронного двигателя с переменными 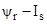 в произвольной системе координат на основе интегрирующих звеньев // Молодой ученый. — 2015. — № 15 (95). — С. 7-30.
в произвольной системе координат на основе интегрирующих звеньев // Молодой ученый. — 2015. — № 15 (95). — С. 7-30.
6. Медведев А.В., Емельянов А.А., Клишин А.В. Математическая модель асинхронного двигателя в неподвижной системе координат с переменными ir – ψr // Молодой ученый. — 2010. — №4. — С. 8-24.
7. Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.

