В статье представлены результаты программной реализации математической модели в системе компьютерной математики (СКМ) MathCad для определения параметров, а также исследования режимов работы индукционной тигельной печи с трехсекционным индуктором на конечных этапах плавки.
Ключевые слова: индукционный нагрев, индукционная тигельная печь, многосекционный индуктор.
Требование обеспечения возможности управления силовым воздействием электромагнитных полей на ванну жидкого металла для организации управляемого перемешивания металла на разных стадиях технологического процесса плавки является чрезвычайно важным требованием к системе электропитания при индукционной плавке. Одним из наиболее перспективных способов повышения управляемости является секционирование индуктора [1].
В данной работе реализован алгоритм расчета математической модели системы индукционной тигельной печи с трехсекционным индуктором, при разработке которой был принят ряд допущений [1].
Исследуемая система «трехсекционный индуктор — нагреваемое изделие» представляет собой однородный металлический цилиндр, помещенный в три многовитковые секции, по которым протекает переменный ток. Данная система рассматривается как множество колец прямоугольного сечения, не имеющих полости внутри (рис. 1).
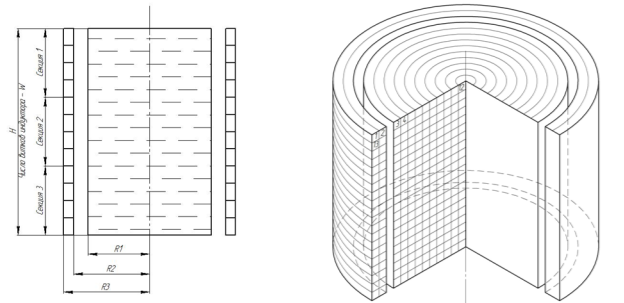
Рис. 1. Разбиение системы «трехсекционный индуктор — нагреваемое изделие» на кольца прямоугольного сечения
Кольца, на которые разбита рассматриваемая система, представляются индуктивно взаимосвязанными контурами (рис. 2). На основе таких контуров построена математическая модель системы «трехсекционный индуктор — нагреваемое изделие».
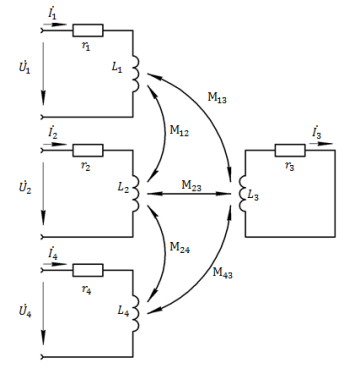
Рис. 2. Индуктивная взаимосвязь контуров на примере трёх колец индуктора и одного кольца загрузки
Для автоматизированного расчета математической модели разработана программа расчета в (СКМ) MathCad. На первичном этапе работы программы задаются исходные данные индуктора и нагреваемого материала. В ходе расчета определяются необходимые параметры схемы замещения многосекционного индуктора, а также данные режима работы установки.
Разработанная программа позволяет в автоматизированном режиме построить систему уравнений по законам Кирхгофа для каждого контура и решить её. На основе системы уравнений строится матрица T (рис. 3, а). Выше и ниже главной диагонали матрицы T располагаются взаимные индуктивности колец. Главная диагональ матрицы представляет собой полные сопротивления колец системы.
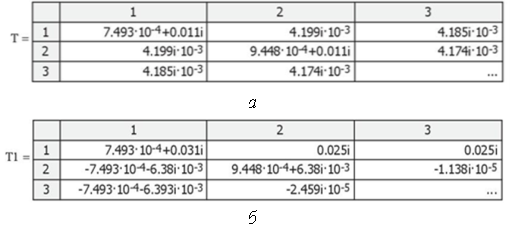
Рис. 3. Полученная матрица коэффициентов системы T (а), преобразованная затем в матрицу для вычисления токов колец T1 (б)
Матрица T преобразуется в матрицу коэффициентов при токах T1, в которой исключены неизвестные напряжения колец и добавлены уравнения, описывающие взаимную связь между токами витков индуктора, а также между входным напряжением индуктора и падениями напряжения на каждом из витков индуктора (рис. 3, б). Для исключения дополнительных неизвестных падения напряжения на каждом из витков индуктора выражены через токи колец и их сопротивления. С помощью матрицы T1 вычисляются искомые токи каждого кольца системы ![]() (рис. 4).
(рис. 4). ![]() — столбец свободных коэффициентов.
— столбец свободных коэффициентов.

Рис. 4. Вектор токов каждого кольца системы, преобразуемый в вектор модулей токов (а) и вектор токов в каждом из витков индуктора (б)
По найденным значениям токов каждого кольца системы построены характеристики распределения плотности токов в индукторе и нагреваемом изделии в виде гистограмм (рис. 5).
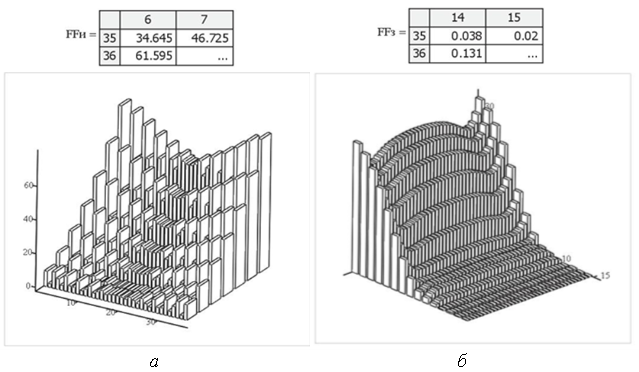
Рис. 5. Модули полученных токов и их распределение для каждого кольца в индукторе (а) и нагреваемом изделии (б)
Также в виде гистограммы построена характеристика, показывающая распределение напряжения на каждом витке индуктора (рис. 6).
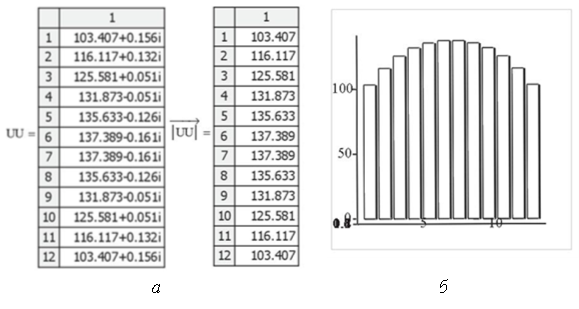
Рис. 6. Вектор напряжений на витках индуктора, преобразуемый в вектор модулей напряжений (а) и распределение модулей напряжений на каждом витке индуктора (б)
Реализация данного алгоритма позволяет в автоматизированном режиме рассчитывать математическую модель [1], получая все необходимые данные (токи каждой секции, токи каждого контура, напряжения витков и т. д.) для дальнейшего исследования модели и проверки её корректности.
Литература:
1. Сергеев Д. А. Разработка математической модели системы «многосекционный индуктор — нагреваемое изделие» установки индукционного нагрева // Труды Академии электротехнических наук Чувашской республики 2015

