В работе построена семимартингальная модель динамики нормального суточного профиля артериального давления, разработанная на основе данных суточного мониторинга.
Ключевые слова: семимартингал, артериальное давление, процесс Орнштейна-Уленбека, мультивариантный процесс, точечный процесс.
На сегодняшний день математическое моделирование широко используется в биологии и медицине как актуальный и эффективный метод решения прикладных задач. Особый интерес для научных исследований представляют математические модели сердечно-сосудистой системы человека [2–4].
В статье разработана математическая модель нормального суточного профиля артериального давления (АД) в семимартингальных терминах. В семимартингальном описании заключается специфика и новизна данной модели. Разработанная вероятностная модель является новой и актуальной для решения прикладных задач биологии и медицины.
Статистический анализ данных.
Исследование суточного профиля АД проводилось в лаборатории артериальной гипертонии Ульяновского клинического госпиталя ветеранов войн. По результатам суточного мониторирования артериального давления (СМАД) и дополнительного медицинского обследования у 144 пациентов не было выявлено сердечно-сосудистых патологий. Мониторирование проводилось с использованием носимого АД-монитора «BPLab МнСДП-3» (ООО «Петр Телегин», Нижний Новгород).
Согласно анализу экспериментальных данных, в активный период кривая циркадианного ритма АД имеет два пика, первый наблюдается в интервале 
, второй — в интервале 
. Третий пик приходится на ночное время, в интервале 
, при этом средние ночные значения АД должны быть ниже средних дневных на 10–20 %. Далее в период 
начинается утренний подъем АД. На каждом из четырех промежутков циркадианный ритм АД представляет собой выпуклую вверх функцию. В настоящей работе в качестве таких функций рассматриваются синусоиды. Параметр 
— момент начала СМАД, выбираемый, как правило, в утреннее или послеполуденное время до 14:00. Параметр 
— момент завершения эксперимента, в большинстве случаев приходится на утренние часы. Моменты времени 
, 
и 
определяются по экспериментальным данным.
Математическая модель нормального суточного профиля артериального давления
Пусть на стохастическом базисе 
задан непрерывный случайный процесс 
, описывающий нормальную суточную динамику АД.
Процесс Y представляет собой сумму детерминированной и стохастической составляющих:
,
где детерминированная функция 
— циркадианный ритм АД, а случайный процесс V — вариабельность АД. Время t измеряется в часах. Параметры 
и T — моменты начала и окончания эксперимента.
Математическая модель циркадианного ритма АД имеет вид:
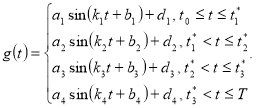
Параметры 
и 
определяются на основе реальных данных. Значения неизвестных параметров 
, 
, 
, 
, 
, найдены с помощью методов оптимизации (например, метода наименьших квадратов). При этом функция 
должна удовлетворять следующим требованиям:
1) Непрерывность 
на отрезке 
.
2) Выпуклость вверх 
на каждом из четырех промежутков 
, 
, 
и 
, где параметры 
, 
и 
представляют собой моменты времени 
, 
и 
, переведенные в количество часов.
Случайный процесс V представляет собой сумму смещенного процесса Орнштейна-Уленбека D и процесса M, совершающего скачки в случайные моменты времени:
Случайный процесс 
задается как
где параметр сдвига a вычисляется как среднее арифметическое суммы разностей между экспериментальными данными после выбраковки значительных колебаний АД и значениями функции 
в соответствующих узловых точках.
Процесс Орнштейна-Уленбека 
является решением уравнения Ланжевена [1]
с начальным условием 
где 
— неотрицательная случайная величина с конечной дисперсией. Параметр 
— коэффициент линейного роста, параметр 
— коэффициент диффузии. Процесс 
— винеровский с начальным значением 
.
Траектории случайного процесса 
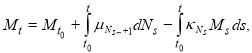
с начальным условием 
. Случайный процесс 
— произвольный точечный процесс с нулевым начальным значением 
. Последовательность 
— независимые равномерно распределенные на 
случайные величины, 
. Значения параметров 
и 
определяются экспериментально. В связи с тем, что процесс M не совершает скачков в начальный момент времени 
, и до момента первого скачка значения процесса M равны нулю, в качестве 
рассматривается 
. Последовательность 
— независимые положительные случайные величины
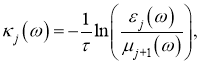
где параметр 
вычисляется на основе экспериментальных данных, а 
— последовательность независимых положительных случайных величин, удовлетворяющих условию 
для любого 
. Начальное значение 
.
Процесс M — семимартингал, совершающий скачки в моменты скачков считающего процесса N. Значения траекторий процесса M интерпретируются как значительные колебания уровня АД, вызванные стрессовыми воздействиями. Каждый скачок процесса M совершается в случайный момент времени 
(момент скачка процесса N) на случайную величину 
, 
. Случайные величины 
характеризуют скорость спада АД после каждого значительного скачка.
Заключение
На основе экспериментальных данных разработана семимартингальная модель нормального суточного профиля артериального давления. Данная концепция может найти применение в медицине при изучении гомеостатических систем организма, диагностике нарушений суточной кривой артериального давления пациента, а также в учебно-исследовательской деятельности бакалавров и магистров физико-математического и медицинского факультетов.
Литература:
- Бутов А. А. Элементы стохастического исчисления / А. А. Бутов. — Ульяновск: УлГУ, 1996. — 25 с.
- Воронин И. М. Циркадный ритм артериального давления у здоровых людей и его прогностическое значение [Электронный ресурс] / И. М. Воронин, Е. А. Баженова // Естествознание и гуманизм: сб. научн. трудов; ред. Н. Н. Ильинских. — Томск, 2006. — Т. 3, вып. 4. — С. 67–68. — Режим доступа: http://www.tele-conf.ru/files/raznoe/EG-3–4-2006.rar (дата обращения: 20.04.2018).
- Разин В. А. Предикторы эффективности антигипертензивной терапии у больных гипертонической болезнью: дис.... канд. мед. наук: 14.00.06. — Самара, 2004. — 148 с.
- Цфасман А. З. Циркадная ритмика артериального давления при измененном суточном ритме жизни (работе в ночное время): монография / А. З. Цфасман, Д. В. Алпаев. — 2-е изд., испр. и доп. — М.: Репроцентр М, 2011. — 144 с. — ISBN 978–5-94939–059–7.
