В статье описывается процесс разработки графа клеточных взаимодействий для исследования трёхмерных моделей структуры живых тканей. Описываемое программное обеспечение позволяет строить и исследовать такие модели, созданные в рамках теории трёхмерной гистологии (разработанной Г. А. Савостьяновым), которые невозможно построить с помощью текущих средств.
Ключевые слова: клетка, геометрический центр, граф клеточных взаимодействий, 3D гистология.
Гистология — раздел биологии, изучающий строение тканей живых организмов. Для классической гистологии является традиционным изучение структуры тканей, основанное на изучении её двумерных срезов. Эти методы, однако, не дают верного представления о трёхмерной структуре ткани, поэтому современные специалисты изучают геометрические особенности отдельно взятых клеток.
Геннадий Александрович Савостьянов описывал подход к 3D моделированию структуры биологической ткани [1]. Он ввёл понятие гистион, как элементарную единицы многоклеточности. Гистионы — это группы клеток, которые возникают в результате разделения функций между клетками. Пласты рассматриваются как регулярные клеточные решетки, образующиеся путём полимеризации гистионов. Также Севастьянов предлагает подход к описанию возникновения стволовых клеток в развитии многоклеточных организмов [2]. Основа подхода — форматизированное описание становления гистионов путём приобретения и реализации потенций для осуществления процедуры разделения функций между клетками.
Важным аспектом для изучения является пространственная организация тканей, т. е. внутреннее расположение клеток в ткани. Существует гипотеза, что при патологиях (например, раковой опухоли), происходит изменение не клеток, а структуры ткани, т. е. взаимного расположения клеток относительно друг друга, а также и способа взаимодействия клеток между собой. Исследования, ищущие причины рака внутри клеток, являются неудачными, что может косвенно подтверждать эту гипотезу.
В связи с этим, появилась необходимость построения графа клеточных взаимодействий.
Графом клеточных взаимосвязей (или «этажеркой») является представление топологии клеточной сети пласта в целом (Рис 1).

Рис. 1. Сенсорный эпителий органа слуха голубя и представление решетки в виде графа клеточных взаимосвязей
В таком виде у модели можно рассмотреть, каким образом связан каждый уровень друг с другом. Легче становится проследить непосредственно за изменением или нарушением отношений между клетками внутри одного гистиона.
Идея построения
Каждая клетка в программе состоит из нескольких слоёв. Построение «этажерки» заключается в том, чтобы каждый слой представить в виде вершин графа, которые затем будут соединены ребрами. В пределах одной клетки построить её представление в виде графа не составляет труда. В пределах гистиона это уже сложнее, т. к. приходится применять определённые методы для того, чтобы определить, находятся ли рядом с рассматриваемой клеткой ещё одна для того, чтобы связать их вершины рёбрами.
Для построения «этажерки» используется следующий алгоритм:
- Рассчитывается центр каждого отдельно взятого слоя.
- Вершины в пределах одной клетки соединяются рёбрами.
- Для каждой клетки происходит поиск рядом лежащих клеток.
- Достраиваются межклеточные рёбра.
Геометрический центр
Геометрический центр, или барицентр [3] — это среднее арифметическое положение всех точек фигуры. Фигуры, образующие слои клеток, могут состоять как из одной точки, так и из нескольких. Для каждого случая необходимо находить геометрический центр по координатам точек.
Определение местоположения барицентра для конечного множества точек.
Барицентр конечного множества из k точек ![]() в
в ![]() находится по формуле:
находится по формуле:
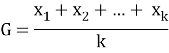
Полученная G такая, что сумма расстояний между точками множества и ней является минимальной.
Промежуточный результат выполнения алгоритма можно наблюдать на Рис 2. В пункте 3 ставится задача поиска для каждой клетки клеток, с которыми она граничит. Необходимо понять, какие вершины потребуется соединить ребрами.
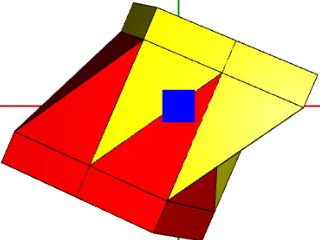
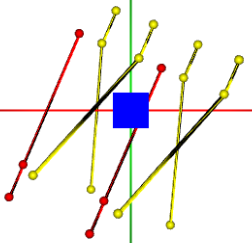
Рис. 2. Гистион и его отдельное представление его клеток в виде графа клеточных взаимосвязей
Процесс нахождения соседних клеток
Для того, чтобы реализовать для каждой клетки поиск её соседей, нужно понять, как они стыкуются. Выполнятся следующее правило: клетка A стыкуется на уровне (слое) n с клеткой B на её уровне (слое) m, если n и m имеют хотя бы две общие вершины. Вершины считаются общими, если расстояние между ними <0,1. В случае, если слой n или m состоит из одной вершины, клетки считаются соприкасающимися на этом уровне. Таким образом проверяются все вершины каждой клетки и, в зависимости от результата проверки, строятся рёбра.
Итогом работы алгоритма является построенный граф структурных взаимосвязей клеток (Рис 3).
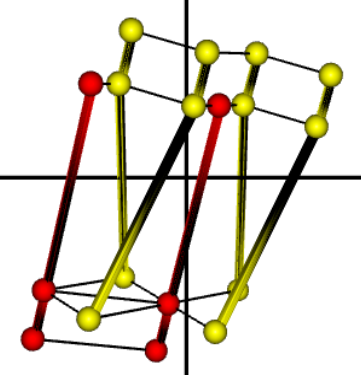
Рис. 3. Гистион, представленный графом клеточных взаимодействий
Литература:
1. Савостьянов Г. А. Возникновение элементарных единиц многоклеточности и формирование пространственной организации клеточных пластов, 2012. 165 с.
2. Савостьянов Г. А. Возникновение стволовых клеток в развитии многоклеточности и их количественная характеристика, 2016. 557 с.
3. Барицентр // Свободная энциклопедия википедия URL: https://ru.wikipedia.org/wiki/Барицентр (дата обращения: 07.04.2019).







