В связи с большой популярностью применения теплообменных аппаратов, появляется необходимость в их совершенствовании. Одним из главных показателей является эффективность теплообменника, которая выражается в первую очередь в высокой эффективности теплообмена. Добиться повышения эффективности теплообмена можно с помощью различных манипуляций. Одной из самых распространенных является применение интенсификаторов, одним из которых является оребрение на стенках канала. В данной работе оребрение рассматривается на плоском канале. Модель канала была выбрана по типу каналов, применяемых в регенераторах с непосредственной теплопередачей для газотурбинных установок, работающих по открытому циклу. Геометрические размеры плоского канала и параметры рабочей среды, приняты, как в примере, предложенном авторами пособия [1].
Канал представляет собой прямоугольный параллелепипед шириной 229 мм, длиной 1830 мм и высотой 6.35 мм. На стенках по всей длине расположены прямоугольные ребра: ширина ребра — 3 мм, высота — 1.5 мм (рис.1). Для выполнения работы была построена расчетная область в соответствии со схемой канала. Моделирование осуществлялось на бесплатной облачной платформе [2].
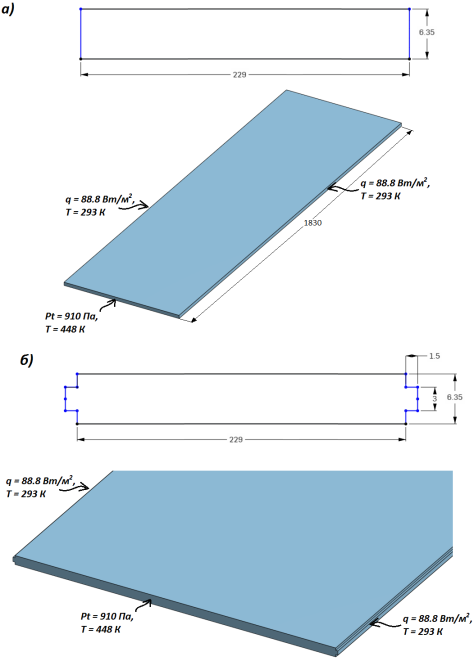
Рис. 1. Геометрия плоского канала а) без ребер; б) с ребрами
Численное моделирование проводилось в облачном сервисе [3]. Была выбрана модель для несжимаемого газового потока в стационарной постановке с использованием модели турбулентности k-omega SST.
Математическая модель включала:
– уравнения движения и сохранения импульса Навье-Стокса;
– уравнение сохранения энергии в стационарной постановке;
– уравнение состояния.
Для моделирования каналов было создано две расчетных сетки типа Hex-dominant (only CFD) в режиме Moderate (рис.2). Общее количество трехмерных элементов сетки составило 236224 для канала без ребер и 401744 для канала с ребрами соответственно.
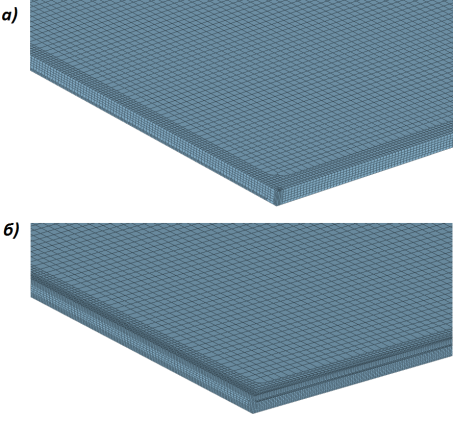
Рис. 2. Расчетная сетка для канала а) без ребер; б) с ребрами
В качестве рабочего тела был использован воздух. Плотность среды составила 1.2 кг/м3. В начальный момент времени были заданы следующие параметры турбулентности: турбулентная кинетическая энергия k=0.00375, м2/с2 и интенсивность рассеивания ῲ=3.375 1/c.
Заданные граничные условия представлены на рис.1:
– Вход: давление — 910 Па, температура — 448 К.
– Выход: давление — 0 Па.
– Стенки: начальная температура — 293 К, удельный тепловой поток — 88.8 Вт/м2.
Параметры расчета: величина временного шага, 
– 1 с; количество итераций, N — 30000; интервал сохранения — 200 с; количество расчетных процессов, n — 8.
Анализ итерационной сходимости решения проводился на основании значений невязок при решении основных уравнений математической модели. Полученная динамика невязок (рис.3) свидетельствует о стабилизации решения после 200-го шага в канале без лунок и 300-го шага в канале с лунками.
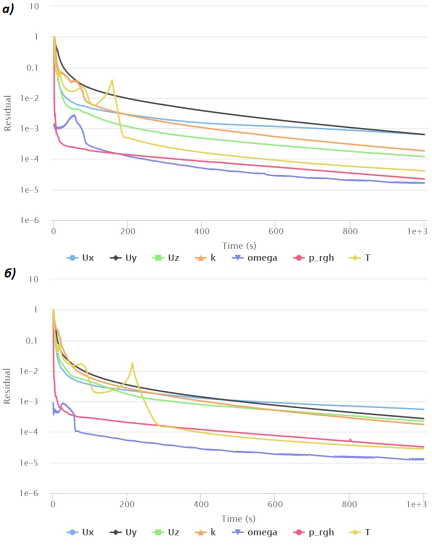
Рис. 3. Динамика невязок в канале а) без ребер; б) с ребрами
Обработка результатов численного моделирования проводилась в бесплатной программе [4], распространяемой по свободной лицензии, в модуле визуализации ParaView. Были использованы параметры температуры на стенке канала и параметры скорости и температуры в центре потока. С помощью численного моделирования был получен профиль скорости (рис.4).
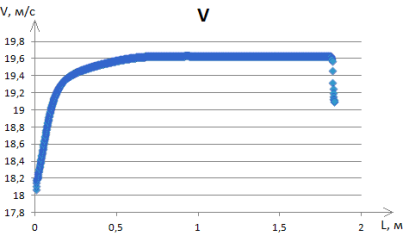
Рис. 4. Профиль скорости
Затем, используя эти данные, были найдены значения α и St, по формулам:
α = Q/ΔT и St = α/(V·ρ·cp),
где Q — удельный тепловой поток, Вт/м2; ΔT — разница температур на стенке канала и в центре потока, К; V — скорость воздуха, м/с; ρ — плотность воздуха, кг/м3; cp — удельная теплоемкость воздуха, Дж/(кг·К).
Полученные значения α и St были отражены на графической зависимости по длине канала (рис.5).
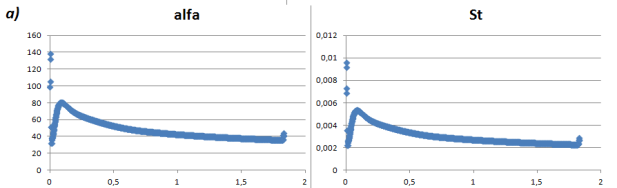
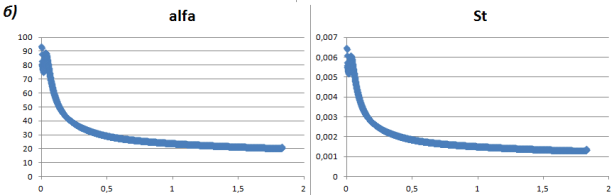
Рис. 5. Графики α и St по длине канала а) без ребер; б) с ребрами
На графиках наблюдаются небольшие скачки. Это связано с неравномерным распределением температуры стенок на входе в канал.
Чтобы сравнить гидравлические потери напора в каналах, необходимо определить значения коэффициентов сопротивления ξ и Сfp. Для этого воспользуемся следующими формулам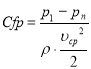и:
и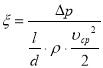 
,
где ∆р — перепад давления в потоке, Па; l — длина канала, м; d — диаметр канала, м; ρ — плотность воздуха, кг/м3;
— средняя скорость воздуха в потоке, м/с.
Затем, для сравнения, строим графики зависимости полученных значений по длине канала (рис.6).
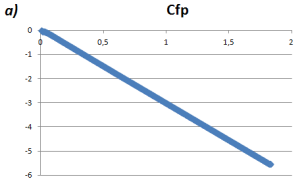
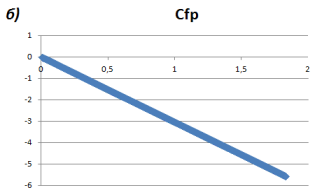
Рис. 6. Графики зависимости Cfp по длине канала а) без ребер; б) с ребрами
График расположен в отрицательной шкале графика.
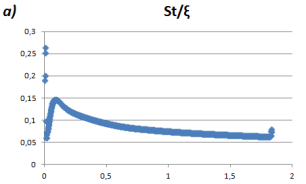
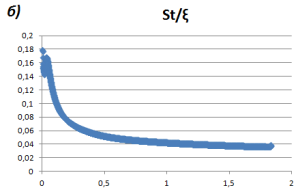
Рис. 7. St/ξ по длине канала а) без ребер; б) с ребрами
Характер кривых совпадает с кривыми на графике рис. 5.
Литература:
- Кэйс В. М., Лондон А. Л. Компактные теплообменники, М.: Энергия, 1967, ст. 208.
- Электронный ресурс. Onshape. Home page. URL: https://www.onshape.com/
- Электронный ресурс. SimScale. Home page. URL: https://www.simscale.com/
- Salome Platform. Home page. URL: http://www.salome-platform.org/
