В данной работе приводится исследование аварийных переходных процессов при помощи точечной математической модели ядерного реактора, включающей в себя уравнения нейтронной кинетики и уравнения теплопроводности между компонентами активной зоны: топливом и теплоносителем. Для связи этих уравнений предполагается, что скорость изменения электрической мощности будет соответствовать скорости изменения нейтронного потока. Уравнения нейтронной кинетики основаны на уравнении баланса нейтронов Больцмана. Вводится двухгрупповое диффузионное приближение. По мимо мгновенных нейтронов рассматриваются и запаздывающие нейтроны. Далее путем мультипликативного разделения переменных можно перейти к решению задачи без учета пространственной зависимости и рассматривать поведение параметров реакторной установки только во времени. Уравнения теплопроводности по топливу и теплоносителю основываются на балансе энергии вырабатываемой и передаваемой компонентами активной зоны. Вводится дополнительное уравнение обратных связей по параметру реактивности, которое позволяет замкнуть систему таким образом, чтобы она была устойчива по отношению к изменению постоянных коэффициентов.
Предполагается решить полученную систему обыкновенных дифференциальных уравнений относительно изменения постоянных коэффициентов в течении времени аварийного режима работы реакторной установки [3]. В нашем случае обеспечить достаточную аппроксимацию позволяет семейство явных методов Рунге-Кутта. В ходе исследования начальных коэффициентов возникает проблема решения жестких систем дифференциальных уравнений [1]. Для этого подбирается параметр сходимости численного решения к точному с расчетом устойчивости системы дифференциальных уравнений на основе критерия жесткости [2], [4]. Решение данной проблемы позволяет применять вышеописанную систему в области потока частиц высоких энергий, которые характеризуются малым промежутком времени жизни. Ранее данная модель использовалась только в энергетической области тепловых нейтронов.
Объектом исследования стал плотностной эффект реактивности или сокращенно ПЭР, связанный с большим количеством аварий в прошлом из-за попадания в область активной зоны воздушных пузырей. Воздушные прослойки, образующиеся вокруг оболочек твэлов, имеют пагубное влияние на систему: плохо замедляют нейтроны и препятствуют теплопередаче между топливом и охладителем. Плотностной эффект реактивности реализуется при частичном осушении жидкого теплоносителя в активной зоне ядерного реактора. Эффект возникает при попадании в рассматриваемую среду газовых пузырей вследствие, например, разгерметизации трубок твэлов или канала теплоносителя в первом контуре. Воздушная полость замещает часть объема, занимаемого теплоносителем, что сопровождается уменьшением среднего значения плотности теплоносителя по активной зоне.
При постоянстве нейтронно-физических и теплогидравлических коэффициентов, указанных в таблице 1, и изменении среднего значения плотности теплоносителя в объеме активной зоны γ/γ0 проведем расчет скачка параметров реакторной установки: относительной мощности φ, температуры топлива ΔTт, изменение температуры теплоносителя ΔTтн и общей реактивности системы ρ.
Таблица 1
Коэффициенты динамической системы
|
Наименование |
Обозначение |
Размерность |
Величина |
|
Время жизни мгновенных нейтронов |
τ |
сек |
7 · 10–6 |
|
Доля запаздывающих нейтронов |
βэф |
% |
64 · 10–4 |
|
Постоянная времени ядер-предшественников |
λ |
сек-1 |
7.84 ·10–2 |
|
Коэффициент реактивности по температуре топлива (U-Pu) |
ξт |
˚К-1 |
5 · 10–7 |
|
Коэффициент реактивности по температуре теплоносителя (свинец) |
ξтн |
˚К-1 |
3 · 10–7 |
|
Коэффициент реактивности связанный с плотностью теплоносителя |
ξγ |
г-1 · см3 |
1 · 10–6 |
|
Номинальная мощность реактора |
Qэл0 |
МВт |
3 · 106 |
|
Высота активной зоны |
Hа.з. |
см |
70 |
|
Диаметр топливного элемента |
dт |
см |
0.96 |
|
Количество топливных элементов (твэлов) |
Nт |
шт. |
100 |
|
Плотность топлива |
γт |
г · см-3 |
14.3 |
|
Плотность теплоносителя (свинец) |
γтн |
г · см-3 |
11 |
|
Теплоемкость топлива (U-Pu) при постоянном давлении |
cтp |
Дж·г-1 · ˚К-1 |
0.27 |
|
Теплоемкость теплоносителя (свинец) при постоянном давлении |
cтнp |
Дж·г-1 · ˚К-1 |
0.147 |
|
Коэффициент теплопередачи |
αт |
Вт · см-2 · ˚К-1 |
2.6 |
|
Температура теплоносителя на входе в активную зону |
Tтнвх |
˚К |
650 |
|
Температура теплоносителя на выходе из активной зоны |
Tтнвых |
˚К |
773 |
|
Расход теплоносителя |
Gтн |
г · с-1 |
9 · 104 |
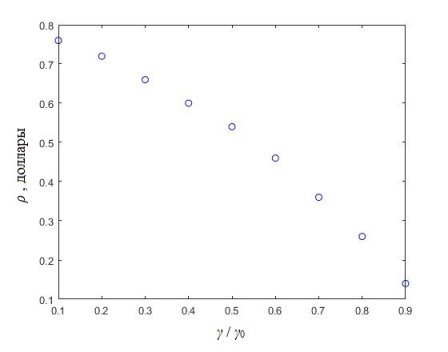
Рис. 1. Скачок параметра реактивности ρ (в долях запаздывающих нейтронов)
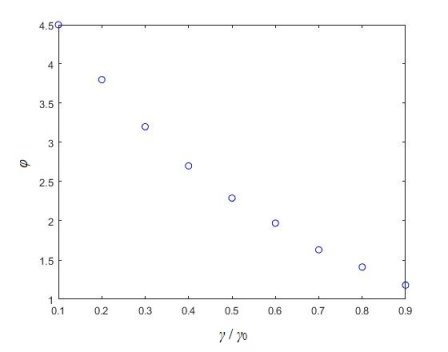
Рис. 2. Скачок параметра относительного энерговыделения φ
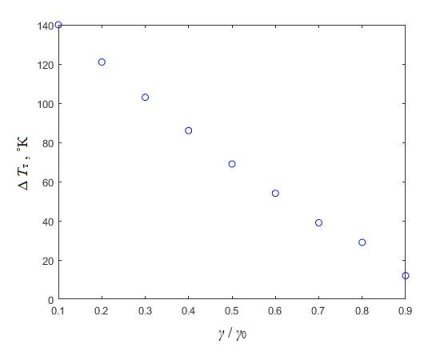
Рис. 3. Скачок температуры топлива ΔTт, ˚К
При возникновении плотностного эффекта реактивности и уменьшении значения плотности теплоносителя до 0,1 г · см-3 реактивность системы в течении первых 5 секунд испытывает резкий рост до 0,8 долей запаздывающих нейтронов, скачок электрической мощности реакторной установки составляет 4,5 номинального значения (рис. 2), скачок температуры топлива равен 140 ˚К (рис. 3). Температура теплоносителя вовремя ПЭР не испытывает резких изменений. Также стоит обратить внимание на тенденцию уменьшения времени роста реактивности, при которой время достижения максимального значения реактивности при 90 % снижении значения плотности теплоносителя составляет 1,7 секунды, в то время как при снижении плотности до 10 % время, за которое скачок достигает своего максимального значения составляет 0,7 секунды. Аналогично с параметром относительного энерговыделения: при 90 % время возрастания равняется 1,9 секунды, при 10 % — 0,7 секунды.
Стоит отметить, что численные результаты показали также появление второго резкого изменения значений параметров реакторной установки при уменьшении плотности теплоносителя на 50 % и более. Подобно первому скачку, вновь образованный имел незначительный рост относительно первого, а время достижения второго максимума снижалось при уменьшении относительного значения плотности теплоносителя.
Рассмотрим случай, когда реализуется плотностной эффект реактивности, при котором половина всего объема охладителя замещается воздухом, тогда среднее значение плотности по объему активной зоны равно 5,5 г · см-3. Исследуем каким образом изменение расхода теплоносителя повлияет на величину скачка мощности и реактивности.
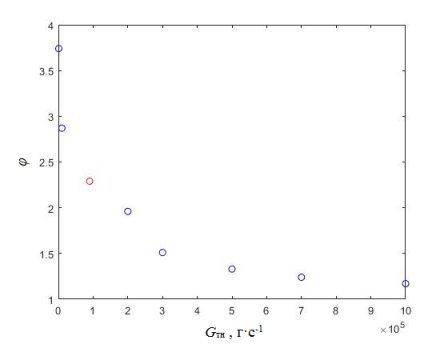
Рис. 4. Зависимость расхода теплоносителя от скачка мощности
Согласно данным с рис. 4, воздушный пузырь при низком значении расхода 103 г · с-1 обеспечивает скачок мощности реакторной установки, как в случае, когда расход равен 9 · 104 г · с-1, но при среднем значении плотности 0,2 от номинального значения рис. 2. Если наоборот увеличивать расход до 106 г · с-1, то возникает ситуация, при которой скачек такой же, как и в случае 0,9 от номинального значения плотности теплоносителя.
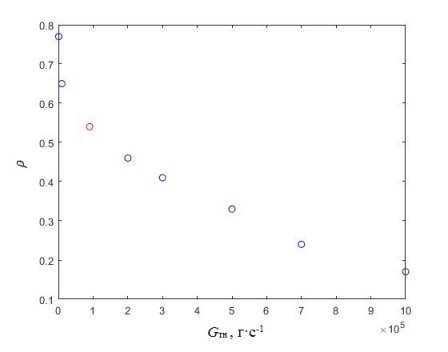
Рис. 5. Зависимость расхода теплоносителя от скачка реактивности
На рис. 5 представлена величина скачка реактивности при различных значениях параметра расхода. Реактивность напрямую связана с величиной удельного энерговыделения как показано в уравнениях нейтронной кинетики. Путем увеличения расхода теплоносителя можно подобрать наилучший вариант развития аварийного перехода вследствие плотностного эффекта реактивности.
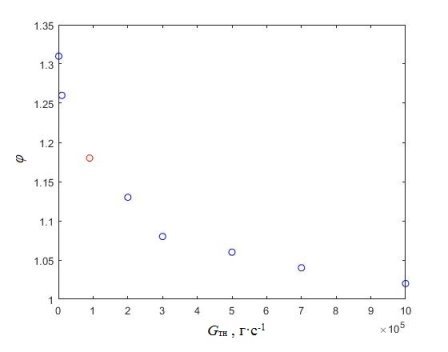
Рис. 6. Зависимость расхода теплоносителя от уровня установившейся мощности
При постоянном объеме и сниженной массе охладителя в активной зоне может потребоваться серьезное увеличение скорости транспортировки.
Показано, что во избежание «разгона» реактора посредством усиления деления ядер топлива на мгновенных нейтронах при возникновении положительного пустотного эффекта реактивности, сопровождающегося снижением среднего значения плотности с 10,5 до 5,5 г · см-3 достаточно увеличить расход теплоносителя в десять раз (для достижения наилучшего результата). Полученный закон изменения установившейся мощности от расхода теплоносителя, представленный на рис. 6, позволяет сделать вывод о том, что при малом расходе теплоносителя возникают значительное увеличение уровня электрической мощности в 4 и более раз.
Литература:
- Галанин М. П., Ходжаева С. Р. Методы решения жестких обыкновенных дифференциальных уравнений. Результаты тестовых расчетов // Препринты ИПМ им. М. В. Келдыша. — 2013. — № 98. — 29 с.
- Коношенко А. В. Об устойчивости систем линейных дифференциальных уравнений второго, третьего и четвертого порядка / А. В. Коношенко, Г. С. Родионова // Современные проблемы науки и образования. — 2013. — № 4. — с. 307.
- Кузьмин А. М. Моделирование физических процессов в энергетических ядерных реакторах на быстрых нейронах: учебное пособие для вузов / А. М. Кузьмин, А. Н. Шмелев, В. А. Апсэ. — М.: Издательский дом МЭИ, 2013. — 128 с.: ил.
- Новиков Е. А. Внутренняя устойчивость явных методов Рунге-Кутта / Е. А. Новиков, Ю. А. Шитов // Вестник Красноярского государственного аграрного университета. — 2007. — № 2. — с. 54–58.

