Инновации в образовании – естественное и необходимое условие его развития в соответствии с постоянно меняющимися потребностями человека и общества. Способствуя, с одной стороны, сохранению традиционных ценностей, с другой стороны, инновации несут в себе отказ от всего устаревшего и отжившего, формируют основы социальных преобразований.
Одним из вариантов модернизации системы образования может быть макрологический подход. В настоящее время в литературе элементы макрологического подхода к изучению инновационных процессов встречаются в трудах Н.И. Лапина, А.И. Пригожина, Б.В. Сазонова, В.С. Толстого [1]. Суть макрологического подхода состоит в фокусировании на взаимодействия инновационных процессов: их сочетании, конкуренции, последовательной смене.
В рамках макрологического подхода выделяется принцип дополнительности как необходимое условие взаимодействия инновационных образовательных процессов. Суть принципа дополнительности заключается в том, что для адекватного описания существующего объекта требуется описывать его во взаимоисключающих понятиях. Культурологическое значение принципа дополнительности было показано В. В. Налимовым, как аллегория идеи полиморфизма языка. «Рассуждения человека должны быть, с одной стороны, достаточно логичными, они должны базироваться на дедуктивной логике, с другой стороны, они должны быть построены так, чтобы допускались логические переходы типа индуктивных выводов и правдоподобных заключений, не укладывающихся в стройную логику системы постулатов и правил вывода» [2, с. 32]. В. В. Налимов определяет философскую значимость принципа дополнительности, которая состоит в том, что мышление человека богаче его дедуктивных форм [3, с. 234].
Мы предлагаем рассмотреть проблему формирования такого мышления у учащихся общеобразовательных учебных заведений, мышления, выходящего за рамки оперирования дедуктивными формами при разрешении проблемных ситуаций – инновационного мышления. Аспекты этого вопроса можно встретить в работах Ю.П. Саламатова [4]. Его формирование может быть одной из сторон модернизации современного обучения.
Инновационное мышление самопроизвольно не формируется и не является общепризнанным, как и предшествующие способы мышления (оперирование числами и символами вместо самих реальных объектов, использование письменности и т.д.).
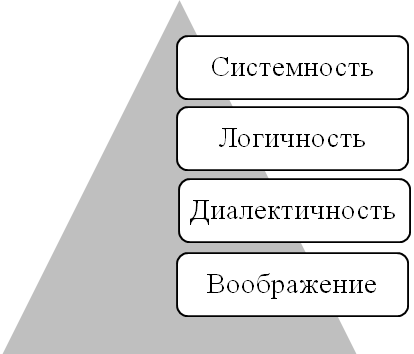
Выделяют базис такого мышления [5]: системность: логичность; диалектичность; воображение. Каждый из этих компонентов должен тесно основываться на творческом потенциале мышления как способности человека к созданию инновации (рис. 1).
Рис. 1. Базис инновационного мышления
Системность. Любая инноватика есть либо усовершенствование существующей какой-либо системы либо создание новой, ранее не существующей. В окружающем мире все взаимосвязано, и любой объект одновременно является элементом другой более крупной системы и одновременно сам есть целостная система со своими элементами.
Логичность. Использование аппарата традиционной логики незаменимо при решении простейших творческих «повседневных» задач.
Диалектичность. Создание нового не может быть основано на традиционной логике. Для его создания необходимо преодолеть препятствие – разрешить противоречие.
Воображение. Только человеческий мозг обладает таким свойством. История культуры в целом это история человеческого воображения. Умение представлять несуществующие объекты, находить связи между самыми отдаленными, на первый взгляд, объектами задача воображения.
Подробнее рассмотрим формирование инновационного мышления у школьников в общеобразовательных учебных заведениях.
С одной стороны, для развития логичности и воображения предложено немало методов и инструментов, которые успешно развивают их. С другой стороны, большинство школьников не применяют логику в творческом процессе, позволяющую проверять обоснованность либо парадоксальной либо сгенерированной идеи, не могут управлять своим воображением в случае необходимости при разрешении проблемы и т.д. Проблема заключается в использовании методов обучения, не учитывающих целость, единство и взаимосвязь элементов инновационного мышления.
Во второй половине XX века сформировалась как научное направление ТРИЗ (теория / технология решения изобретательских задач) Г. С. Альтшуллера [6]. Исторически, сутью ТРИЗ является целенаправленный поиск решения, совмещенный с отбором из предполагаемых вариантов наиболее сильных без сплошного перебора слабых. Области современного ТРИЗ весьма широки: в построении сюжетов литературных произведений, живописи, искусстве (Ю. Мурашковский, С. В. Козловский, О. Алешина и др.), в биологии (В. А. Бухвалов, И. Н. Самаль, В. И. Тимохов, И. Андржеевская и др.), в математике и методике математического развития (А. А. Страунинг, В. М. Цуриков, А. В. Козлов, Т. В. Погребная и др.), в физике (А. Гин и др.), в географии (Т. В. Иванова и др.), в педагогике и психологии (А. Н. Тубельский, Н. Н. Хоменко, И. С. Якиманская, С. Ю. Модестов, Ю. Г. Тамберг, М. Н. Шустерман, З. Г. Шустерман и др.), в теории опережающей педагогики (М. И. Меерович, Л. П. Шрагина), в бизнесе (В. Г. Сибиряков, С. В. Сычев, О. И. Сычева и др.), в рекламе (И. Л. Викентьев) и т.д. Ряд наработок позволяет применять инструменты ТРИЗ при обучении в общеобразовательной школе.
Можно с достаточной эффективностью использовать элементы ТРИЗ в учебном процессе для развития элементов инновационного мышления. Эффективность отдельных приемов убедительно была доказана в ходе экспериментальной работы по применению ТРИЗ в педагогике [7, 8, 9, 10, 11, 12].
В рамках нашего исследования для развития инновационного мышления мы используем задачи открытого типа [13]. Учебные задания, моделирующие ситуации, являющиеся неразрешимыми (в субъективном смысле относительно ученика), значительно приближены к открытым задачам. Такие задачи предусматривают возможность применения стандартных знаний в нестандартной ситуации, при выполнении таких заданий ученик может проявить способность к логическому и абстрактному мышлению, то есть умение классифицировать, обобщать и проводить аналогии, прогнозировать результат, применяя интуицию, воображение и фантазию.
Следует сказать несколько слов о различиях между закрытыми и открытыми задачами.
Закрытые задачи. Задачи данного типа предусматривают четкую и однозначную трактовку условий решения проблемы, из которой, зачастую, единственный способ напрашивается сам собой. В результате задача имеет, как правило, одно правильное решение. Такие задачи не дают возможности ребенку в полной мере проявлять и развивать свои творческие способности (творческие – в широком смысле понимания). Задания данного типа хороши для отработки какого-либо конкретного приема решения, при изучении нового материала и являются основой традиционной парадигмы образования, зачастую способствуют игнорированию творческого потенциала ребенка.
Открытые задачи. Задачи открытого типа имеют размытое условие, из которого недостаточно ясно, как действовать, что использовать при решении, но понятен требуемый результат. Такие задачи предполагают разнообразие путей решения, которые не являются прямолинейными, двигаясь по которым попутно приходиться преодолевать возникающие препятствия. Вариантов решений много, но нет понятия правильного решения: решение либо применимо к достижению требуемого результата, либо нет.
Приведем примеры закрытых и открытых задач.
Задача 1. Выделите части слова «мухоловка»?
Анализ. Вспоминаем необходимые определения, применяем их – и ответ готов. Перед нами задача с четким условием, содержащая все необходимые данные. Метод решения известен, да и ответ единственный. Поэтому эта задача закрытого типа.
Задача 2. «Еж в яблоках». С детства знакомая картинка: еж, несущий на своих иголках яблоко. Куда и зачем он его несет? Зоологи утверждают, что яблоки ежи не едят – они насекомоядные! Тем более, что на зиму никакое пропитание им не требуется – в это время они спят, как медведи или барсуки. И наконец, было замечено, что они выбирают наиболее кислые яблоки.
Анализ. Задача имеет размытое условие, не ясно, чем пользоваться при ее решении. Контрольных вариантов решений достаточно много.
- С помощью кислот, которые есть в кислых яблоках, ежи борются с паразитами, которые находятся на их иголках.
- Ежи не едят яблоки, они едят насекомых. Но, может быть, яблоки служат хорошим кормом для насекомых, которые на яблоках размножаются? Ежи, таким образом, запасают еду для насекомых, а потом их едят.
- Ежи выбирают кислые яблоки. Может быть, им нужна кислота для нейтрализации щелочей, которая, возможно, выделяется через колючки.
- Яблоки гниют, при этом выделяют энергию. Возможно, ежи используют энергию гниения, чтобы во время спячки, когда температура тела животных понижается, в норке зимой поддерживалась плюсовая температура.
- Ежи с помощью яблок подчеркивают свое превосходство для привлечения партнера. Подобно тому, как это делают петухи с помощью гребня или павлины с помощью хвоста.
Выше сказанное дает нам право считать эту задачу открытой.
Учитывая нестандартность задач, а, следовательно, и всю сложность оценки заданий творческого характера, нами были выбраны и апробированы следующие критерии оценки задач открытого типа.
-
Эффективность решения (достигнуто ли требуемое в
задаче?)
Оценка
Критерий
0
По решению не ясно, как можно достигнуть искомого результата
1
В целом ход решения понятен, и результат так достигнуть можно, но некоторые моменты решения не продуманы или нечетко объяснены
2
Предложенное решение позволят четко понять, как достигнуть результата
- Оптимальность (оправдано ли
такое решение?)
Оценка
Критерий
0
Решение слишком громоздкое; использование множества приемов не оправданно
1
Решение оптимально, но некоторые моменты процесса решения можно значительно упростить
2
В решении использован тот или иной метод, благодаря которому получилось достаточно емкое, четкое и оптимальное «красивое» решение
- Оригинальность (ново ли
решение, или решение обыденное?)
Оценка
Критерий
0
Решение стандартное, встречается более чем у 10% школьников
1
Решение встречается в ответах редко: от 5 до 10 % школьников
2
Решение оригинальное встречается менее чем у 5% школьников
- Разработанность (достаточно ли подробно описан ход решения, или решение на уровне идей?)
|
Оценка |
Критерий |
|
0 |
Не описан или непонятен ход решения задачи |
|
1 |
Решение описано на уровне идей, которые возможно довести до разумного конца |
|
2 |
Четко и грамотно описано решение и обоснованы все действия |
Приведем пример использования предложенных критериев в конкретной ситуации.
Задача 3. «О соответствии». Порой в жизни мы не выполняем арифметические операции с числами: вряд ли кто-то скажет, что знания отличника равны сумме знаний двоечника и троечника (5=2+3), или, чтобы Вы сказали о человеке, который занимается сложением цифр в телефонных номерах? Приведите 3-4 примера, где числа используются в жизни не для вычислений.
Анализ. Можно выделить контрольные решения: номер паспорта, дома; на футболках спортсменов; номера магазинов, школ; в школе, получая оценки; возраст и т.д.
Критерии оценки
-
эффективность решения (достигнуто ли требуемое в
задаче?)
Оценка
Критерий
0
Нет примеров или всего один
1
Есть два примера
2
Есть более трех примеров
- оптимальность (оправдано ли
такое решение?)
Оценка
Критерий
0
Есть примеры, но все они из одной области жизни (например, все из школьной действительности)
1
Есть примеры, хотя бы из двух разных областей жизни (например, школа и спорт)
2
Все примеры из разных областей жизни
- оригинальность (новое ли
решение, или решение обыденное?)
Оценка
Критерий
0
Решение стандартное, встречается более чем у 10% школьников
1
Решении встречается в ответах редко: от 5 до 10% школьников
2
Решение оригинальное встречается менее чем у 5% школьников
- разработанность (достаточно ли подробно описан ход решения, или решение на уровне идей?)
|
Оценка |
Критерий |
|
0 |
Нет примеров |
|
1 |
Есть примеры, но нет никаких пояснений |
|
2 |
Приведены примеры и есть пояснения (почему именно этот ответ отвечает требованиям решения проблемы) |
Наличие положительных результатов в формировании инновационного мышления у учащихся общеобразовательных школ при апробации открытых задач позволяет говорить о возможности их использования для повышения эффективности модернизации образования, а также при разработке единых принципов и подходов к формированию целей, постановке задач и прогнозированию результатов модернизации.
- Литература:
- Блейхер О.В. Взаимодействие инновационных образовательных процессов как необходимое условие модернизации образования при становлении постиндустрильного общества [Электронный ресурс]/ О.В. Блейхер // Управление общественными и экономическими системами: сборник материалов научной конференции / Орловский государственный технический университет, 2006г. / Режим доступа: http://elibrary.ru/item.asp?id=9288713. Дата обращения: 10.09.2009
- Налимов В.В. Вероятностная модель языка. О соотношении естественных и искусственных языков. 3 издание. Томск: Водолей, 2003. 368 с.
- Руднев В.П. Принцип дополнительности // Словарь культуры ХХ века. М.: Аграф, 1997. 384 с.
- Саламатов Ю.П. Основы инновационного мышления [Электронный ресурс] / Ю.П. Саламатов // Институт инновационного проектирования, г. Красноярск, 2009г. / Режим доступа: http://rus.triz-guide.com/club.html. Дата обращения: 09.12.2009
- Саламатов Ю.П. Основы инновационного мышления: презентационный материал. [Электронный ресурс] / Ю.П. Саламатов // Институт инновационного проектирования, г. Красноярск, 2009г. / Режим доступа: http://rus.triz-guide.com/assets/files/DY.pdf. Дата обращения: 09.12.2009
- Альтшуллер, Г.С. Найти идею. Введение в теорию решения изобретательских задач / Г.С. Альтшуллер. – 2-е изд., доп. – Новосибирск: Наука. Сиб. отд-ние, 1991. – 225 с.
- Педагогика + ТРИЗ [Текст]: сборник статей для учителей, воспитателей и менеджеров образования. №1-6. – Мн.: ПолиБиг, 1997 – 2001г.
- Учителям о ТРИЗ. Выпуск 1 -5 [Текст]: сборник методических материалов по преподаванию ТРИЗ. – Спб.: Союз писателей Санкт Петербурга 1999-2006г.,.
- Ширяева, В.А. Развитие системно-логического мышления учащихся в процессе изучения теории решения изобретательских задач (ТРИЗ) [Текст]: автореф. дис. канд. пед. наук / В. А. Ширяева. – Саратов: СГУ им. Н. Г. Чернышевского, 2000. – 18 с.
- Модестов, С Ю. Проектирование образовательных технологий на основе ТРИЗ [Текст]: автореф. дис. канд. пед. наук: 13.00.01 / С. Ю. Модестов; СПб: РГПУ им. А.И. Герцена, 2001. – 18 с.
- Терехова, Г.В. Творческие задания как средство развития креативных способностей школьников в учебном процессе [Текст]: автореф. дис. канд. пед. наук: 13.00.01 / Г. В. Терехова. – Челябинск, 2002.
- Фёдорова, Е.А. Развитие творческой активности студентов средствами ТРИЗ-педагогики (на примере изучения информатики) : автореф. дис. на соиск. учен. степ. канд. пед. наук: 13.00.01: защищена 22.12.09 / Фёдорова Е.А.-Ульяновск:[б. и.],2009.-22 с.
- Утёмов, В. В. О творческих задачах и критериях их оценивания [Текст] / В. В. Утёмов // Материалы Всероссийской научно-практической конференции «Подготовка специалистов в системе непрерывного профессионального образования: проблемы и перспективы». – Киров: Изд-во ВятГГУ, 2009. – С. 219-223.