Пространственное мышление является существенным компонентом в подготовке к практической инженерной деятельности по специальности «Технология машиностроения» в техническом вузе. Практика обучения на первых курсах вуза такой дисциплины как начертательная геометрия постоянно обнаруживает слабое развитие пространственного мышления студентов. Студенты часто не справляются с задачами как теоретического, так и практического характера, в связи с отсутствием специфического вида мыслительной деятельности, а именно пространственного мышления. В своих наиболее развитых формах это есть мышление образами, в которых фиксируются пространственные свойства и отношения.
Пространственное мышление является сложным процессом, в котором происходят следующие действия (рисунок 1):
Рисунок 1 – Процесс работы с образами
Образы здесь являются и исходным материалом, и основной оперативной единицей, и результатом мыслительного процесса. Это не означает, конечно, что при этом не используются словесные знания. В образном мышлении слова используются как средства интерпретации уже выполненных в образах преобразований [2].
Содержанием пространственного мышления является оперирование пространственными образами на основе их создания с использованием наглядной опоры (предметной или графической, разной меры общности и условности). Эти особенности пространственного мышления отражают процесс работы с образом и выявляют его качественное своеобразие. Формы и уровни пространственного мышления определяются с одной стороны, объективным содержанием материала, а с другой стороны – познавательной активностью студента.
|
||||
|
||||
Рисунок 2 – Формы и уровни пространственного мышления
Объективное содержание материала включает в себя наглядность, доступность. В процессе обучения начертательной геометрии необходимо широко пользоваться наглядными учебными пособиями: плакатами, моделями, деталями, различными изделиями, чертежами и т. д. Рекомендуется также использование при чтении лекций раздаточного материала, применение компьютерного учебника и других современных технических средств обучения.
Применение компьютерного учебника на занятиях начертательной геометрии позволяет при существенном повышении темпа обучения повысить качество знаний в связи с развитием таких психических процессов, как память и пространственное мышление, и, как следствие, повысить интерес к начертательной геометрии.
Познавательная активность студентов, реализуется в процессе решения задач, требующих создания пространственных образов и оперирования ими. Уровень этой активности зависит от овладения студентами средствами деятельности, т.е. способами представливания. При оперировании образом мысленно видоизменяется уже созданный на этой основе образ, нередко в условиях полного отвлечения от него.
Важнейшим условием, обеспечивающим формирование представлений о геометрических образах, является обучение учащихся приемам рассмотрения и запоминания их, а также и приемам их воспроизведения по памяти. Процесс формирования пространственных представлений о геометрических объектах проходит на основе знаний о них [4].
На практических занятиях студенты должны обучаться приемам анализа предметов: мысленного ее расчленения на геометрические тела, из которых она состоит, и выделения всех ее элементов. Это в свою очередь требует мысленного проведения границ каждого геометрического тела (там, где в предмете эти тела не разграничены).
Кроме того, нахождение геометрических тел предъявляет требования к приемам абстракции: учащиеся должны мысленно выделить в каждом геометрическом теле его существенные признаки. Так, например, студенты под руководством преподавателя рассматривают предмет, как неделимую совокупность геометрических тел и их частей между собой. Студенты должны сказать, из каких элементов состоит тот или иной предмет, и обозначить их существенные признаки.
Важнейшим принципом, направленным на обучение, является следующее положение: в начале усвоения нового материала в курсе начертательной геометрии и инженерной графики учащиеся обучаются элементарным приемам, которые характеризуются дополнительной опорой на наглядный материал. Затем методика должна обеспечить перестройку приемов так, чтобы студент создавал образы без дополнительной опоры, т.е. мысленно, деятельностью воображения – от конкретного созерцания к абстрактному мышлению. Переход учащихся от действий с дополнительной опорой к мысленным при формировании образов воображения выявляет закономерность, состоящую в том, что в усвоении знаний и умений большую роль играет переход от фактических действий, или действий с наглядным материалом, к мысленным действиям, т. е. к действиям в уме.
Этот переход должен осуществляться своевременно. Если студентов слишком долго обучать «наглядным» способам учебной работы, не включающим деятельность воображения, то это может в дальнейшем затруднить развитие их пространственных представлений [1].
Затем учащиеся обучаются приемам создания образов с помощью деятельности воображения. Преподаватель должен предложить воспроизвести мысленно те действия, которые студенты выполняли фактически, при усвоении наглядного приема:
– представить трехгранный угол-октант и находящуюся в нем точку, прямую, плоскость, геометрическое тело;
– мысленно провести перпендикуляры (спроецировать геометрические образы) на грани трехгранного угла;
– представить проекции геометрических образов на этих гранях;
– повернуть правую и нижнюю грани вокруг своих осей (совместить горизонтальную и профильную плоскости с фронтальной плоскостью проекций);
– представить три проекции геометрических образов.
В этом случае прием создания образа выражается в следующем: студенты создают образы проекций с помощью дополнительных представлений (трехгранного угла-октанта). Это достигается деятельностью воображения. При этом студенты осуществляют переход от фактических действий с наглядным материалом (в предварительном обучении) к мысленным действиям с опорой на дополнительные представления. После этого студенты обучаются более сложному для них приему. Преподаватель ставит перед ними следующую задачу: научиться представлять проекции заданных геометрических образов без опоры на дополнительные образы, т.е. не представляя трехгранный угол. Этот прием создания образа заключается в следующем: рассмотрев условие задачи, мы последовательно мысленно «видим» геометрические образы в ней на плоскости. Иначе говоря, представляем себе три проекции в плоскости тетради и затем вычерчиваем их изображения. Переход к этому способу характеризуется тем, что исчезает опора на дополнительные представления, что связано с усложнением деятельности воображения. При овладении этим способом многие студенты испытывают, серьезные затруднения. Они не могут «увидеть» предмет в «плоскостном виде», т. е. они не могут отвлечься от третьего измерения. Если студентам все же удается представить мысленно ту или иную проекцию геометрического образа (горизонтали, фронтали, плоскости и т.д.), то этот образ легко исчезает или искажается. В целях преодоления трудностей студенты возвращаются к предыдущему приему: они создают образ с помощью дополнительных представлений. При построении графического изображения главной задачей является перевод представления об объекте в плоскостное его изображение, при чтении решается противоположная задача: на основе восприятия плоскостного изображения мысленно, в представлении, воспроизводится форма, размеренность, положение объекта и выясняются необходимые сведения, взаимосвязи и отношения. Представления об объекте при чтении и построении графических изображений формируются не только в результате непосредственного узнавания или припоминания, а в результате целой системы умственных действий, направленных на преобразование данных восприятия и мысленное воспроизведение образа. Чтение и построение нельзя свести непосредственно к навыкам, они являются осмысленными умениями, в которых лишь отдельные действия автоматизированы.
Важное место в курсе инженерной графики, изучаемой сразу после начертательной геометрии, занимает овладение приемами, которые нужны учащимся для дальнейшего создания образов уже при чтении чертежа. Преподаватель объясняет учащимся, что чтение чертежа включает:
– рассмотрение чертежа (включая все его детали и условные обозначения) и соотнесение его элементов по трем проекциям;
– создание образа предмета на основе этого чертежа. Этот последний процесс является сложным и имеет две неразрывно связанные стороны.
Хорошее знание начертательной геометрии предопределяет успешность изучения других графических дисциплин в вузе. Методы начертательной геометрии являются теоретической базой для решения задач технического черчения. В технике чертежи являются основным средством выражения человеческих идей. Они должны не только определять форму и размеры предметов, но и быть достаточно простыми и точными в графическом исполнении, помогать всесторонне, исследовать предметы и их отдельные детали. Для того чтобы правильно выразить свои мысли с помощью рисунка, эскиза, чертежа требуется знание теоретических основ построения изображений геометрических объектов, их многообразие и отношения между ними, что и составляет предмет начертательной геометрии.
Отсюда следует, что эффективное развитие у студентов пространственного мышления в условиях изучения начертательной геометрии на первом курсе возможно:
– при рассмотрении начертательной геометрии как части общечеловеческой культуры и понимания места этой науки в своей дальнейшей профессиональной деятельности;
– при одновременном рассмотрении анализа геометрического содержания задач и содержания конкретной деятельности студента при учете, общих психологических закономерностей процесса формирования пространственного мышления;
– при создании условий успешности обучения.
Для развития пространственного мышления и геометрической интуиции студентов целесообразно:
– установить «место затруднения» каждого студента и его уровень развития пространственного мышления;
– изучать плоские и пространственные формы совместно, проводя аналогии между фактами геометрии, высшей математики, черчения, информатики, фиксируя пространственные свойства и отношения;
– формировать умения оперировать пространственными образами и их отношениями;
– знакомить студентов с пространственными объектами до того, как будет дано их формальное и строгое определение (во время изучения таких тем «Точка», «Прямая», «Плоскость»).
– готовить студентов-первокурсников к восприятию 3D моделирования графического материала через решение системы задач на проекционном чертеже;
– снизить уровень строгости логических рассуждений при обосновании утверждений, очевидных с точки зрения студентов.
Студенты Сарапульского политехнического института на вопрос, какие факторы влияют на успешность обучения при изучении начертательной геометрии (рисунок 3), выделили следующие факторы: пространственные представления, изучение черчения в школе, интерес к дисциплине, сила воли, поддержка преподавателя, настроение. Опрос проводился перед изучением дисциплины, в середине семестра и после сдачи экзамена по начертательной геометрии.
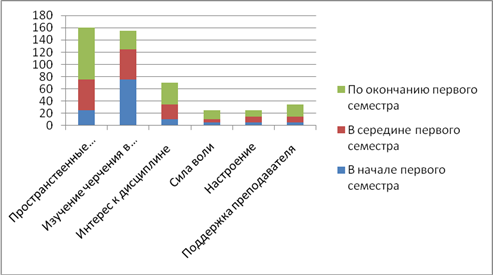
Рисунок 3 – Факторы, влияющие на успешность обучения начертательной геометрии
Проблемой формирования пространственного мышления, пространственного воображения у студентов являются пространственные представления, без которых освоить данный предмет просто невозможно. Развитие воображения – важнейшее условие овладения умением строить и читать чертеж и графической деятельностью в целом. Вместе с тем процесс обучения начертательной геометрии и инженерной графике служит одним из наиболее важных средств развития воображения.
Далее видим, преемственность между школьным курсом черчения и начертательной геометрией в вузе, как фактор, влияющий на успешность обучения начертательной геометрии в вузе.
Значительно менее очевидно, хотя, может быть, гораздо более важную роль в успешности обучения играет воля учащегося. Начинать воспитание воли следует с приобретением привычки решать задачи сравнительно незначительной трудности. Систематически преодолевая сначала небольшие трудности, а со временем и значительные, учащиеся тренируют и закаляют свою волю.
На умственные процессы и, следовательно, на успешность обучения влияет так же ряд факторов, которые с виду не имеют к ним никакого отношения. Это такие стороны личности человека, как эмоции, чувства, настроение в данный момент, темперамент, характер и другие.
Только при условии того, что если задача доступна учащемуся, если цели ее решения ясны, если он чувствует свое движение вперед, то создающиеся при этом положительные эмоции облегчают дальнейшее решение.
Вопрос о влиянии внушения и самовнушения чрезвычайно важен в обучении решению задач. Преподаватель должен проявлять чуткость в своих беседах со студентами. Всевозможные замечания вроде таких, что «у тебя все равно ничего не получится», способны в сильнейшей степени деморализовать студента-первокурсника, который впервые столкнулся с такой задачей как, изображение пространственных тел на плоскости и по плоскому изображению мысленно создавать представление о форме предмета. И наоборот, уверенное убеждение, что «задача должна решиться потому, что ты серьезно занимаешься, а ты не хуже других», во многих случаях сыграет свою положительную роль.
Может быть, еще большую роль играет самовнушение. Если студент почему-то пришел к выводу, что «он не способен», что «ничего не получится», то, конечно, сколько времени он ни сидел бы над задачей, он все равно задачи не решит. Такое самовнушение учащегося парализует его волю, лишает его концентрации мысли, и он не сможет мобилизовать столько энергии на преодоление стоящих перед ним задач, сколько он мог бы проявить в нормальных условиях. В этом случае надо добиться перелома в психике студента-первокурсника, вселить в него уверенность в своих силах, возбудить волю. Возможно, что студенту, потерявшему веру в себя, целесообразно сначала дать для решения самые простые и понятные с первого раза задачи, чтобы дать ему возможность поверить в свои силы.
Успешность в изучении начертательной геометрии способствует развитию пространственного воображения и навыков правильного логического мышления. Также совершенствуется способность студентов – по плоскому изображению мысленно создавать представления о форме предмета и наоборот, создавать изображения мысленно созданных образов, т.е. визуализировать мысль.
Начертательную геометрию нужно изучать, понимая и осмысливая все ее многообразие точных и закономерно-обоснованных способов и методов решения графических задач. А для этого необходимо: работать систематически над изучением теории и закреплением ее практическими задачами, обязательно следуя предложенным этапам усвоения знаний (рисунок 4).
Рисунок 4 – Этапы процесса усвоения знаний
Процесс усвоения знаний включает в себя четыре этапа: понимание, запоминание, применение знаний по правилу и решение творческих задач.
Этапы связаны с деятельностью по распознаванию, воспроизведению, решению типовых и нетиповых графических задач, требующих применения знаний в новых ситуациях. Без последнего этапа процесс обучения остается незавершенным. Поэтому процесс усвоения материала по дисциплине «Начертательная геометрия» должен содержать решение пропедевтических творческих задач [3], которые локально направлены на усвоение соответствующих знаний.
И это, естественно, будет способствовать процессу усвоения знаний по начертательной геометрии и развитию пространственного мышления, без которого в дальнейшем невозможна профессиональная инженерно-творческая деятельность.
Литература:
1 Бабанский, Ю.К. Педагогика / Ю.К.Бабанский. – М.: Просвещение, 2004. – С. 33-37.
2 Возрастные и индивидуальные особенности образного мышления учащихся / Под ред. И.С. Якиманской. – М.: Педагогика, 1989.
3 Гервер, В.А. Творческие задачи по черчению: Книга для учителя / В.А.Гервер – М.: Просвещение, 1991. – 128 с.: ил. – С. 63.
4 Якиманская, И.С. Психологические основы математического образования: Учебное пособие для студ. пед. вузов / И.С.Якиманская. – М.: Академия, 2004. – 320с.
