Исследованию существенного спектра непрерывных и дискретных операторов Шредингера посвящены многие работы (см., например, и , соответственно). В работе доказано, что существенный спектр трехчастичного дискретного оператора Шредингера состоит из объединения не более чем конечного числа отрезков даже в том случае, когда соответствующий двухчастичный дискретный оператор Шредингера имеет бесконечное число собственных значений.

В настоящей работе рассматривается модельный оператор , ассоциированный с системой трех частиц на решетке. Описано местоположение существенного спектра оператора , т. е. выделены двухчастичная и трехчастичная ветви существенного спектра оператора .

Следует отметить, что двухчастичная и трехчастичная ветви существенного спектра трехчастичного непрерывного оператора Шредингера представляют собой полубесконечные прямые и пересекаются. В рассматриваемой нами ситуации непрерывного случая такие ветви существенного спектра оператора заполняют отрезки конечной длины, и они могут не пересекаться, т. е. возникает лакуна. Поэтому необходимо изучать ветви существенного спектра по обе стороны трехчастичной ветви. В работах [3,4], доказано, что рассматриваемые решетчатые операторы не имеют частей существенного и дискретного спектров правее трехчастичной ветви.

Пусть — мерный куб с соответствующим отождествлением противоположных граней. Всюду в работе рассматривается как абелева группа, в которой операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в по модулю , где ℝ и ℤ — множества всех вещественных и целых чисел, соответственно.

Пусть — гильбертово пространство квадратично — интегрируемых (комплекснозначных) функций, определенных на и — гильбертово пространство квадратично — интегрируемых симметричных (комплекснозначных) функций, определенных на .

Рассмотрим трехчастичный модельный оператор , действующий в гильбертовом пространстве , по формуле

.

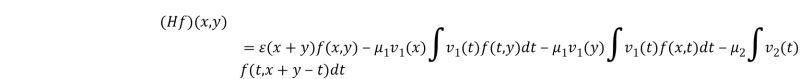Здесь и в дальнейшем интеграл без указания пределов всюду означает интегрирование по всей области изменения переменных интегрирований, — положительные числа, — вещественнозначные непрерывные функции на .

При этих предположениях оператор является ограниченным и самосопряженным в гильбертовом пространстве .

Пусть — комплексная плоскость. При каждом фиксированном определим регулярную в функции

;

,

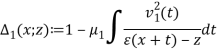где числа и определяются равенствами

, .

Пусть множество тех точек , для которых равенство

имеет место хотя бы для одного и

, ;

, .

Видно, что при каждом фиксированном функция монотонно убывает на полуосях и . Поэтому при всех и верно . Следовательно, для любого функция имеет не более чем один простой нуль, лежащей левее . Отсюда следует, что

.

Следующая теорема описывает местоположение существенного спектра оператора .

Теорема. Для существенного спектра оператора имеет место равенство

.

Вводим новые подмножества существенного спектра оператора .

Определение. Множества и называются, соответственно, двухчастичной и трехчастичной ветвями существенного спектра оператора .

Замечание. Если нечетная функция, т. е.

при всех , то справедливо равенство

.

Очевидно, что если при всех , то из свойства монотонности интеграла Лебега следует, что и . Следовательно, в этом случае двухчастичная ветвь расположена левее трехчастичной ветви существенного спектра оператора . Если при всех , то из свойства монотонности интеграла Лебега следует, что и . В данном случае часть двухчастичной ветви существенного спектра расположено правее трехчастичной ветви существенного спектра оператора .

Если для функции имеет место неравенство

,

то и тем самим появляется часть существенного спектра оператора , правее трехчастичной ветви. Отметим, что появление двухчастичных ветвей по обе стороны трехчастичной ветви существенного спектра оператора играет важную роль при изучении конечности частей дискретного спектра, расположенных там, а также на лакунах существенного спектра.

Автор приносит благодарность к. ф.-м.н., доц. Т. Х. Расулову за постановку задачи и обсуждение результатов работы.

Литература:

1. Г. М. Жислин. Исследование спектра оператора Шредингера для системы многих частиц. Труды Моск. матем. об-ва. 1960, Т. 9, С. 81–120.
2. S.Albeverio, S. N. Lakaev, Z. I. Muminov. On the structure of the essential spectrum for the three-particle Schroedinger operators on lattices. Math. Nachr. 2007, Vol. 280, № 7, Pp. 699–716.
3. S.Albeverio, S. N. Lakaev, R.Kh.Djumanova. The essential and discrete spectrum of a model operator associated to a system of three identical quantum particles. Rep. Math. Phys., 2009, Vol.63, no.3, pp. 359–380.
4. S.Albeverio, S. N. Lakaev, Z. I. Muminov. On the number of eigenvalues of a model operator associated to a system of three — particles on lattices. Russian J. Math. Phys., 2007, Vol.14, no.4, pp. 377–387.