Классификация документов в системе электронного документооборота



В статье описывается методика классификации документов в системе электронного документооборота, основанная на теории алгебры конечных предикатов. Применение предикатов позволяет ускорить процесс отнесения документа к определенному делу в автоматизированном режиме и приписать дополнительные свойства (например, время хранения документа).

Система электронного документооборота (СЭД) — организационно-техническая система, обеспечивающая процесс создания, управления доступом и распространения электронных документов в компьютерных сетях, а также обеспечивающая контроль над потоками документов в организации.

В СЭД для решения таких задач документооборота, как отправка исполненного документа в дело, пересмотр степени ограничения доступа к делу с истечением установленных сроков такого ограничения и др., осуществляется ручная или полуавтоматическая классификация электронных документов. Полуавтоматические решения функционируют на основе математических алгоритмов: деревьев решений, нейросетевых алгоритмов, алгоритма Байеса и др. В статье предлагается методика автоматической классификации электронных документов при распределении их в соответствующие электронные дела, основанная на использовании математического аппарата теории конечных предикатов, проводится сравнительная оценка по времени выполнения операции классификации фиксированного числа документов существующими и предлагаемым алгоритмами.

Теория конечных предикатов включает в себя ряд алгебр, из которых в интересах исследования выделим алгебру конечных предикатов и алгебру предикатных операций [1]. Авторами теории алгебра конечных предикатов позиционируется как универсальное средство формального описания любых объектов, наблюдаемых в мире, и выражения любого отношения. На языке алгебры предикатных операций предпочтительно выражаются действия над отношениями [1, 2].

Из работ Беклемишева Л. Д., Бондаренко М. Ф. и Кругликова Н. П. [1–3] известно, что отношения выражают внутреннее строение объектов, свойства объектов и связи между ними. Они представляют собой универсальное средство формального представления любых объектов. Никакие другие известные средства формального представления объектов свойством универсальности не обладают.

Покажем возможности математического аппарата теории конечных предикатов на примере формализации задачи отправки исполненного электронного документа в электронное дело.

В данном примере в качестве категорий файлов будем использовать иерархию «раздел → дело». В каждом разделе имеется свой набор дел, к которым и будет приписываться классифицированный документ. Пусть множество исполненных документов D={d₁,…,d_|D|}, тогда множество разделов C={С₁,…,С_n}:

С₁ = {a₁₁, a₁₂,…,a_1k1},

С₂ = {a₂₁, a₂₂,…,a_2k2},

…

С_n = {a_n1, a_n2,…,a_nkn},

где a_ij — дело j из раздела С_i, а А = {a₁₁,…,a_nkn} — множество всех дел. Представим алгоритм классификации документа следующим образом. Исполненный документ проверяется на соответствие каждому i-му разделу предикатом P(i, d). Если документ d соответствует описанию раздела С_i, предикат P(i, d), принимает значение «истина»:

Далее при помощи предиката P_v(i,j,d) проверяется соответствие d каждому j-му делу внутри раздела С_i:

Как только P_v(i,j,d) примет значение «истина» (будет определено тематическое соответствие документа делу), перебор останавливается.

Если документ не был классифицирован по разделам при первой проверке, параметры проверки изменяются, либо проверка останавливается и принимается отрицательный результат. Процесс классификации в виде дерева решений приведен на рисунке 1.

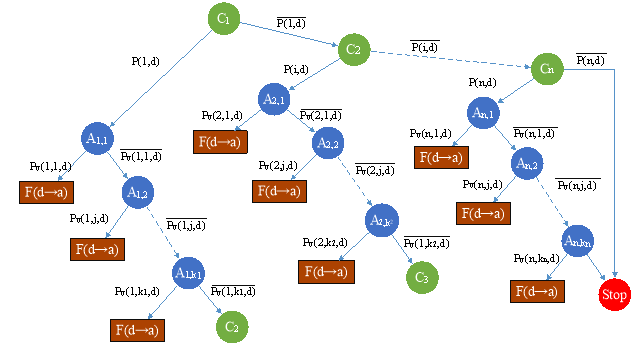Рис. 1. Дерево решений формирования электронного дела

где — функция распределения документов

Как показано выше, для выбора определенного дела необходимо пройти по дереву решений, миновав другие узлы. Следовательно, при переборе узлов необходимо получить отрицательный результат (значение «ложь») предикатов предыдущих итераций. Тогда правило построения предиката определения функции распределения F(d):

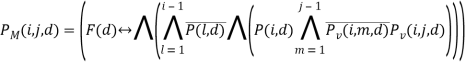
Представим алгоритм классификации в виде блок-схемы в соответствии с теорией алгоритмов (рисунок 2).

Функция распознавания позволяет выполнять классификацию в одномерном массиве вместо двумерного [4]. Это позволяет ускорить обработку: двумерный — O(mk²), одномерный — O(mk). Вычисление пары классификаций для одного объекта с использованием конечного предиката производится единовременно, т. е. нет необходимости проходить каждый узел в отдельности, предикат позволяет проверить ветку за одну операцию (рисунок 2). В качестве дела выбирается первое подходящее в процессе перебора всех веток. Конечные предикаты обладают высокой абстракцией, это позволяет использовать близкие правила как для классификации, так и для распределения дел по признакам. Классификатор на основе предикатов позволяет легко расширять методику отбора. Такой подход позволит адекватно описывать объекты, их свойства и отношения между ними.

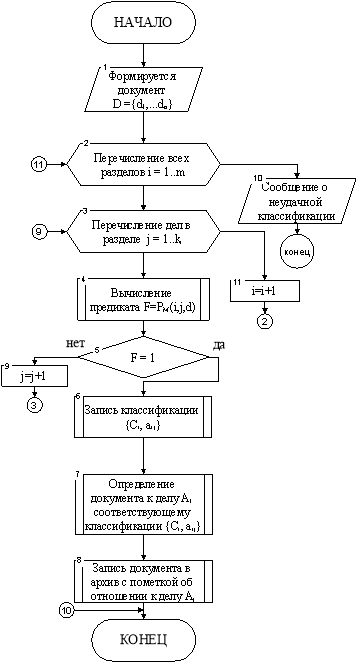
Рис. 2. Алгоритм отнесения документа к делу при помощи предикатов

При рассмотрении описываемой методики классификации важно отметить, как ее сложность зависит от объёма входных данных. В общем случае сложность алгоритма можно оценить по порядку величины [5]. Алгоритм имеет сложность O(f(n)), если при увеличении размерности входных данных N время выполнения алгоритма возрастает с той же скоростью, что и функция f(N). Если общее количество итераций внутреннего цикла равно N*N, это определяет сложность алгоритма O(N^2).

По представленному на рисунке 2 алгоритму можно определить уравнение сложности для него [6]. Использование предикатов при классификации позволяет остановить алгоритм при первом совпадении. Таким образом, ожидаемое количество итераций будет равно mk/2. При каждой итерации, проверяется соответствие документа одним предикатом, который сравнивает критерии и выдает однозначное решение (3 операции).

Приведем таблицу, которая показывает, как долго компьютер, осуществляющий миллион операций в секунду, будет выполнять алгоритмы классификации для одного документа (таблица 1). В качестве сравнения в таблице приведены алгоритмы с построением деревьев решений и байесовский метод.

Таблица 1

Оценка времени выполнения алгоритмов для mk дел

Алгоритм	m*k = 10	m*k = 50	m*k = 100	m*k = 1000	m*k = 10000
Байес O(mk2)	0,6 мс	15 мс	60 мс	6 с	10 мин
Деревья решений O(2mk)	1 мс	18,7 м	40 лет	---	---
Предикаты O(mk)	0,03 мс	0,15 мс	0,3 мс	3 мс	30 мс

Таким образом, алгоритм классификации, построенный на основе предикатов, оказался на порядки быстрей других рассматриваемых алгоритмов (O(N) < O(N²) < O(2^N)).

По результатам исследования в рамках данной статьи можно сделать выводы по качеству и скорости работы алгоритмов классификации:

1. Предлагаемая методика автоматической классификации исполненных электронных документов по электронным делам, построенная с применением теории конечных предикатов, позволяет выполнять классификацию без предварительного обучения и является легко масштабируемой.
2. Данная методика позволяет увеличить качество электронного документооборота — уменьшить время выполнения отдельных операций.

Литература:

1. Бондаренко М. Ф., Кругликова Н. П. Об алгебре одноместных предикатов. // Бионика интеллекта информация, язык, интеллект. Научно-технический журнал № 2 (73) 2010г. — С. 62–68.
2. Бондаренко М. Ф., Шабанов-Кушнаренко Ю. П. Нормальные формы формул алгебры конечных предикатов. // Бионика интеллекта информация, язык, интеллект. Научно-технический журнал № 3 (77) 2011г. — С. 62–68.
3. Беклемишев Л. Д.. Введение в математическую логику. // Мех-мат МГУ, 1-й курс, весна 2008г. Конспект лекций 5 и 6 / Л. Д. Беклемишев.
4. Шитиков В. К., Мастицкий С. Э. Классификация, регрессия и другие алгоритмы Data Mining с использованием R / В. К. Шитиков, С. Э. Мастицкий -: Тольятти, Лондон — 2017г.
5. Галиев Ш. И. Математическая логика и теория алгоритмов. / Ш. И. Галиев — Казань: Издательство КГТУ им. А. Н. Туполева. 2002. -270 с.
6. Алексеева В. А. Использование методов машинного обучения в задачах бинарной классификации. // Автоматизация процессов управления № 3 (41) 2015г. — С. 58–63.