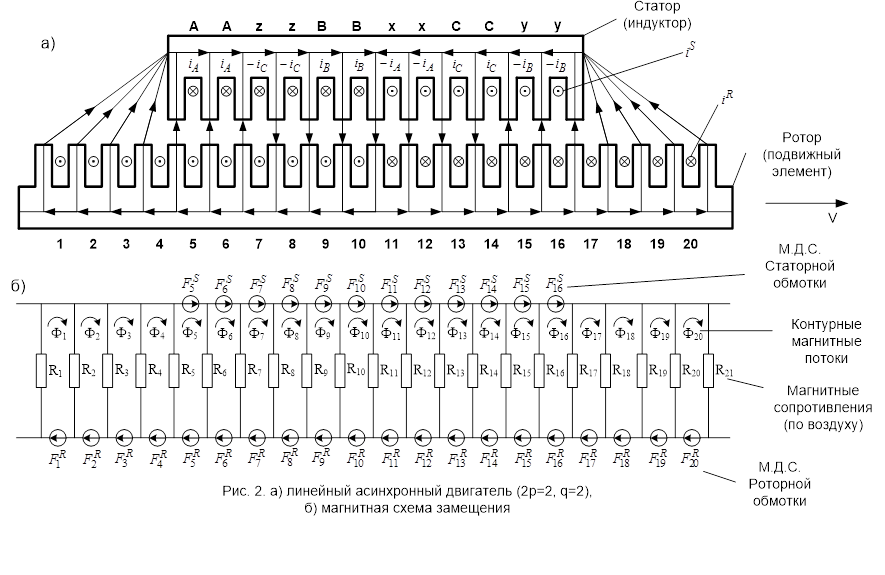
Линейный асинхронный двигатель приведен на рис.2. Расчетная модель представляет собой совокупность развернутых схем замещения магнитной и электрических цепей с частично постоянной аппроксимацией параметров в пределах зубцового деления, которое принимается за основу при разбиении магнитной цепи на участке [1].
Основные допущения:
Ø магнитная проницаемость стальных участков магнитопроводов индуктора и подвижной части (зубцов, ярма) 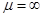 . В магнитной схеме замещения (рис. 1б) учитывается только магнитные сопротивления воздушных участков зазора
. В магнитной схеме замещения (рис. 1б) учитывается только магнитные сопротивления воздушных участков зазора 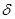 и шунтирующих зон (
и шунтирующих зон (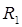 ...
...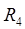 и
и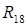 ...
...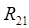 );
);
Ø в шунтирующих зонах как под сбегающим, так и набегающим краем индуктора (статора) учитывается по четыре зубцовых деления подвижного элемента (ротора);
Ø число полюсов индуктора 2р=2; трехфазная однослойная обмотка индуктора с соединением в звезду без нулевого провода; число катушек в катушечной группе равно двум (q=2); намотка катушки производиться в один провод (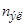 = 1) и число параллельных ветвей а=1.
= 1) и число параллельных ветвей а=1.
Для «n» - го участка схемы замещения запишем основные уравнения:
1. Баланс магнитного напряжения магнитной цепи (рис.1)
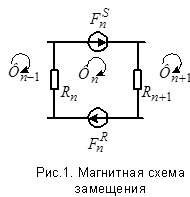
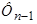 ,
, 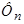 ,
, 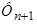 – контурные магнитные потоки;
– контурные магнитные потоки;
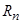 ,
, 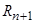 – магнитные сопротивления воздушных участков;
– магнитные сопротивления воздушных участков;
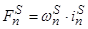 – магнитодвижущая сила, созданная статорным током
– магнитодвижущая сила, созданная статорным током 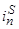 , протекающим по всем проводникам паза (
, протекающим по всем проводникам паза (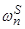 );
);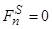 – в шунтирующих зонах;
– в шунтирующих зонах;
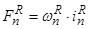 — М.Д.С. тока ротора в стержне (
— М.Д.С. тока ротора в стержне (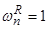 ).
).
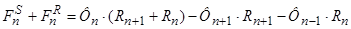
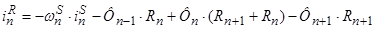 (1)
(1)
2. Уравнение баланса напряжений электрической цепи ротора
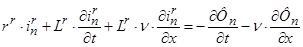 (*)
(*)
Выразим производные во времени через конечные разности:
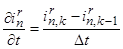 ;
; 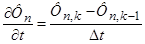
где n – номер зубцового деления;
k – номер шага разбиения по времени.
В формуле (*) скорость подвижного элемента принимается равным 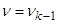 и в пределах «k» интервала считается постоянным.
и в пределах «k» интервала считается постоянным.
Производные по пространственной координате «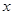 » выразим через центральные конечные разности:
» выразим через центральные конечные разности:
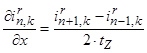 ;
; 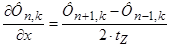
С учетом вышеприведенных замечаний уравнение (*) примет следующий вид:
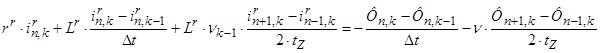 (2)
(2)
Исключим из уравнения (2) токи в роторе, для этого подставим (1) в уравнение (2):
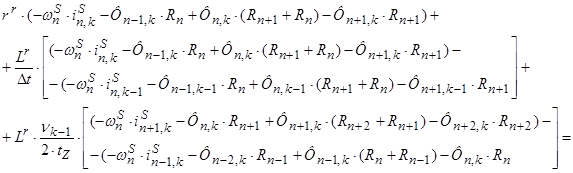
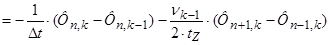
Раскроем скобки:
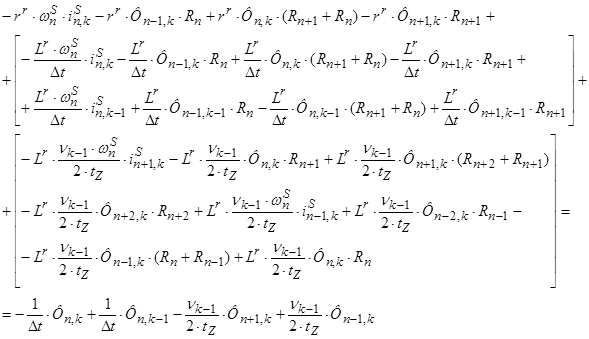
Преобразуем уравнение:
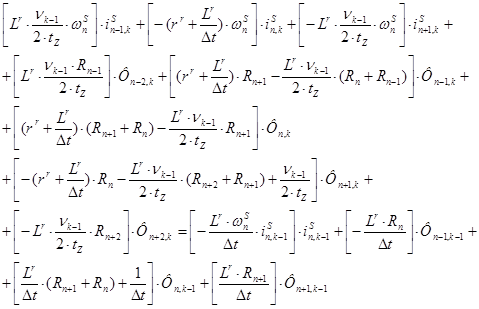
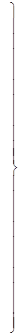 (3)
(3)
Баланс напряжений электрической цепи индукторной (статорной) обмотки
Если питается обмотка индуктора от симметричного напряжения, а схема соединения звезда без нулевого провода, то
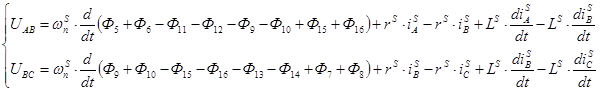 (4)
(4)
где,
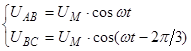 ;
;
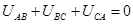
С учетом шага разбиения по времени Δt в к-й момент времени:
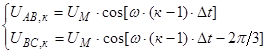 ;
;
Уравнения (4), при выражении производных по времени через конечные разности, примут следующий вид:
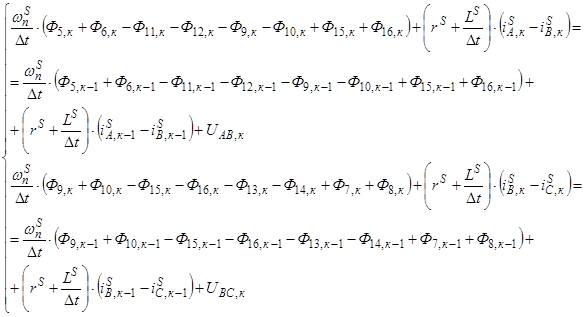 (5)
(5)
При принятых допущениях в системе уравнений будет 23 неизвестных (20 – контурных потоков 3 – тока в фазах обмотки), поэтому решение определяется в матричной форме:
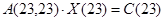 , отсюда
, отсюда 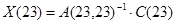 .
.
Обозначим 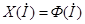 , где
, где 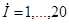 ;
; 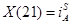 ;
; 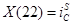 и
и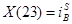 .
.
Для примера рассмотрим формирование нескольких элементов матрицы (Рис.3) для к=1, при следующих параметрах:
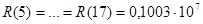 1/Гн;
1/Гн; 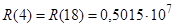 1/Гн;
1/Гн;
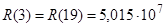 1/Гн;
1/Гн; 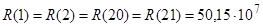 1/Гн;
1/Гн;
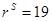 Ом;
Ом; 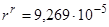 Ом;
Ом; 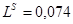 Гн;
Гн; 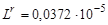 Гн;
Гн; 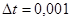 с;
с; 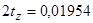 Гн;
Гн; 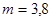 кг.
кг.
При n=1, уравнение (3) примет вид:
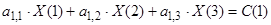 , где
, где 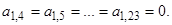
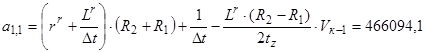
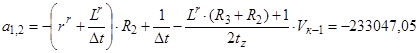 ;
; 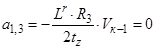
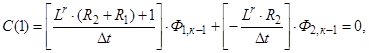
где 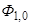 ,
, 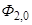 ,
, 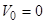
При n=5:
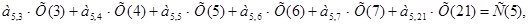
где 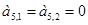 ;
; 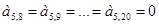 ;
; 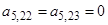 .
.
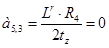 ;
; 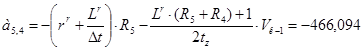
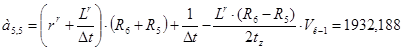 ;
; 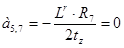
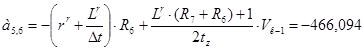 ;
; 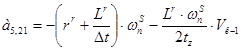
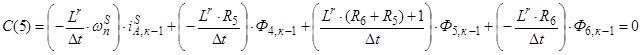
где 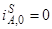 ;
; 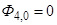 ;
; 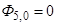 ;
; 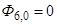 и
и 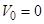 .
.
Элементы матриц А, Х, С для n=21 и n=22 формируются из системы уравнений (5).
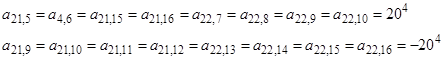
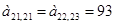 ;
; 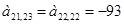 ;
; 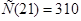 ;
; 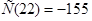
Для строки n=23 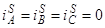 или в матричной форме
или в матричной форме 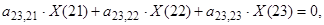 где
где 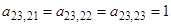 .
.
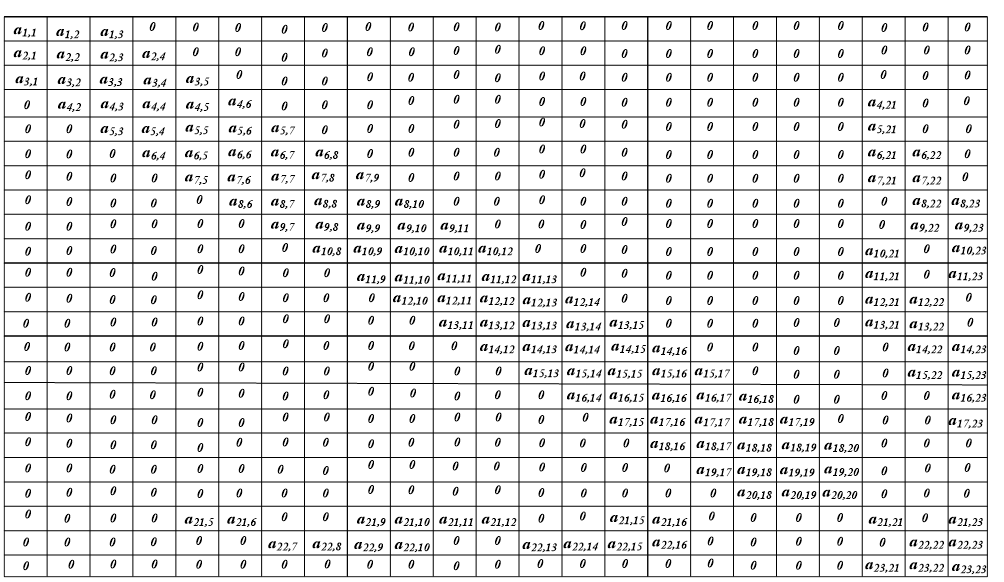 Рис.3. Общий вид элементов матрицы А
Рис.3. Общий вид элементов матрицы А
Для к=1 и к=2 в табл.1 приведены 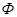 ,
, 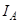 ,
, 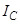 ,
, 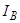 ,
, 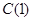 ,
, 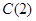 . Кроме того, даны значения токов в стержнях ротора
. Кроме того, даны значения токов в стержнях ротора 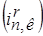 , определенных по уравнению (1) и усилия
, определенных по уравнению (1) и усилия 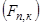 на каждом зубцовом делении.
на каждом зубцовом делении.
Электромагнитное усилие на зубцовом делении определиться по следующей зависимости:
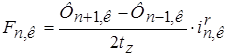 .
.
Суммарное усилие, действующее на подвижный элемент (ротор):
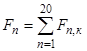
Линейная скорость подвижного элемента:
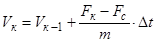
Результаты расчета 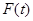 и
и 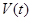 приведены на рис.4.
приведены на рис.4.
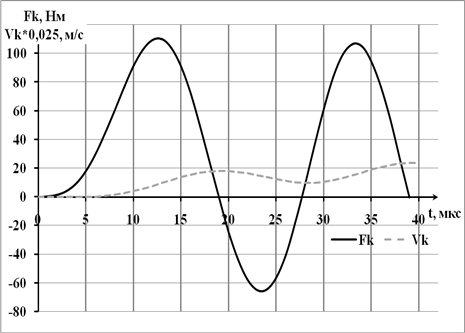
Рис.4. Зависимость электромагнитного усилия и скорости
подвижного элемента от времени при пуске.
Таблица 1.
|
К=1 |
К=2 |
||||||||
|
X |
C |
irn,k |
Fn,k |
X |
C |
irn,k |
Fn,k |
||
|
Ф1 |
7,50E-08 |
0 |
-0,1614 |
-1,24E-06 |
Ф1 |
1,65E-07 |
1,50E-05 |
-0,31 |
-5,30E-06 |
|
Ф2 |
1,50E-07 |
0 |
-0,32 |
-1,38E-05 |
Ф2 |
3,30E-07 |
3,00E-05 |
-0,65 |
-6,06E-05 |
|
Ф3 |
9,10E-07 |
0 |
-1,96 |
-0,00087 |
Ф3 |
2,00E-06 |
1,82E-04 |
-3,91 |
-3,82E-03 |
|
Ф4 |
8,90E-06 |
0 |
-19,15 |
-0,0657 |
Ф4 |
1,94E-05 |
-1,35E-03 |
-44,72 |
-3,42E-01 |
|
Ф5 |
6,79E-05 |
0 |
-146,22 |
-0,4478 |
Ф5 |
1,51E-04 |
1,36E-02 |
-296,34 |
-2,11E+00 |
|
Ф6 |
6,87E-05 |
0 |
-147,95 |
0,4158 |
Ф6 |
1,58E-04 |
1,37E-02 |
-311,19 |
1,53E+00 |
|
Ф7 |
1,30E-05 |
0 |
-28,04 |
0,1198 |
Ф7 |
5,54E-05 |
2,60E-03 |
-113,69 |
9,44E-01 |
|
Ф8 |
-1,47E-05 |
0 |
31,70 |
-0,1413 |
Ф8 |
-3,85E-06 |
-2,94E-03 |
1,95 |
-1,90E-02 |
|
Ф9 |
-7,41E-05 |
0 |
159,46 |
-0,6013 |
Ф9 |
-1,35E-04 |
-1,48E-02 |
258,28 |
-2,23E+00 |
|
Ф10 |
-8,84E-05 |
0 |
190,28 |
-0,1394 |
Ф10 |
-1,73E-04 |
-1,76E-02 |
333,88 |
-9,97E-01 |
|
Ф11 |
-8,84E-05 |
0 |
190,28 |
0,1394 |
Ф11 |
-1,93E-04 |
-1,76E-02 |
377,74 |
5,49E-02 |
|
Ф12 |
-7,41E-05 |
0 |
159,46 |
0,6013 |
Ф12 |
-1,70E-04 |
-1,48E-02 |
333,93 |
2,29E+00 |
|
Ф13 |
-1,47E-05 |
0 |
31,70 |
0,1413 |
Ф13 |
-5,94E-05 |
-2,94E-03 |
121,61 |
1,05E+00 |
|
Ф14 |
1,30E-05 |
0 |
-28,04 |
-0,1198 |
Ф14 |
-4,59E-07 |
2,60E-03 |
6,59 |
6,11E-02 |
|
Ф15 |
6,87E-05 |
0 |
-147,95 |
-0,4158 |
Ф15 |
1,22E-04 |
1,37E-02 |
-232,34 |
-1,49E+00 |
|
Ф16 |
6,79E-05 |
0 |
-146,22 |
0,4478 |
Ф16 |
1,25E-04 |
1,36E-02 |
-239,80 |
1,29E+00 |
|
Ф17 |
8,90E-06 |
0 |
-19,15 |
0,0657 |
Ф17 |
1,69E-05 |
1,78E-03 |
-32,50 |
2,05E-01 |
|
Ф18 |
9,10E-07 |
0 |
-1,96 |
0,00087 |
Ф18 |
1,73E-06 |
1,82E-04 |
-3,34 |
2,84E-03 |
|
Ф19 |
1,50E-07 |
0 |
-0,32 |
1,38E-05 |
Ф19 |
2,87E-07 |
2,99E-05 |
-0,55 |
4,50E-05 |
|
Ф20 |
7,50E-08 |
0 |
-0,16 |
1,24E-06 |
Ф20 |
1,43E-07 |
1,50E-05 |
-0,28 |
4,15E-06 |
|
Ia |
1,02 |
310 |
FΣk |
5,33E-15 |
Ia |
2,11 |
6,05E+02 |
FΣk |
0,228 |
|
Ic |
-1,11E-16 |
-155 |
Ic |
-0,35 |
-2,20E+02 |
||||
|
Ib |
-1,02 |
0 |
Ib |
-1,76 |
0 |
Список литературы:
1. Сарапулов Ф.Н., Емельянов А.А. и др. Исследование электромеханических переходных процессов линейного асинхронного короткозамкнутого двигателя. – Электричество, 1982, №10.







