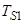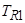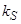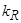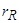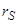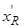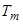Обобщенная асинхронная машина показана на рис. 1 [1] ÷ [3]:
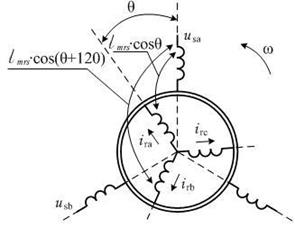

rs, ls, lms – параметры статорной обмотки,
rr, lr, lmr – параметры роторной обмотки,
|lmsr|=|lmrs|=|lm| – коэффициенты взаимоиндуктивности.
Рис.1. Обобщённая асинхронная машина
Основные уравнения математической модели АД в мгновенных значениях переменных:
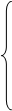
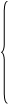
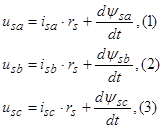
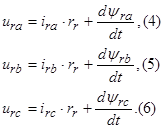
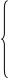
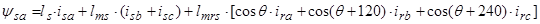
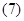
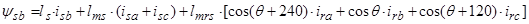
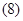
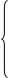
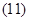
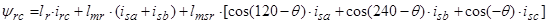
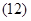
1. Вектор потокосцепления статора АД
Вектор потокосцепления статора является центральным понятием при математическом моделировании асинхронного двигателя, который в дальнейшем будут использован в замкнутых системах векторного управления.
Пространственный вектор потокосцепления статора:
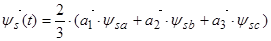 , (13)
, (13)
где 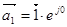 ,
, 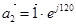 ,
, 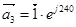 - единичные пространственные векторы.
- единичные пространственные векторы.
Уравнения (7) ÷ (9) представим по трем столбцам соответствующих индуктивностей:

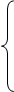
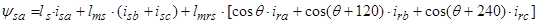
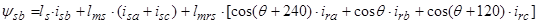
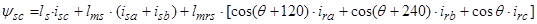
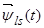
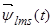
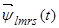
Первое уравнение умножим на единичный пространственный вектор 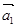 , второе – на
, второе – на 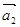 , и последнее уравнение - на
, и последнее уравнение - на 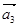 . С целью уменьшения громоздкости получаемых выражений вначале произведем суммирование отдельно по вертикальным столбцам, а затем приведем сумму в соответствии с формулой (13).
. С целью уменьшения громоздкости получаемых выражений вначале произведем суммирование отдельно по вертикальным столбцам, а затем приведем сумму в соответствии с формулой (13).
Мгновенные значения токов в АД:
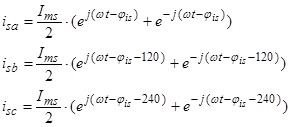
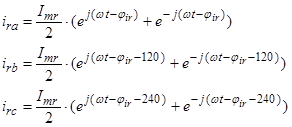
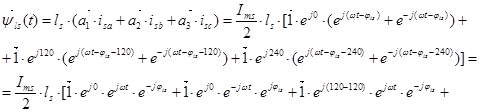
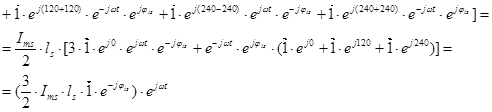
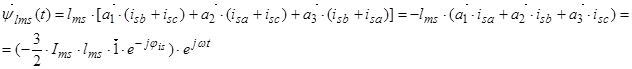
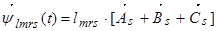 ,
,
где 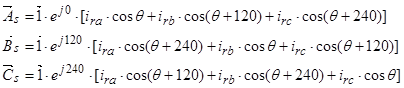 .
.
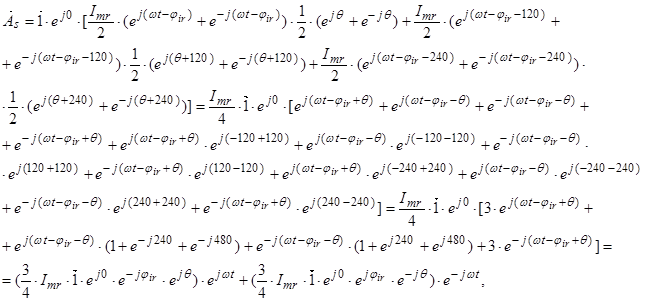 где
где 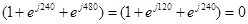
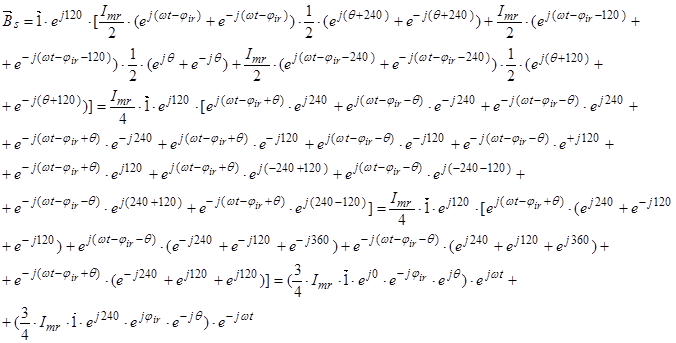
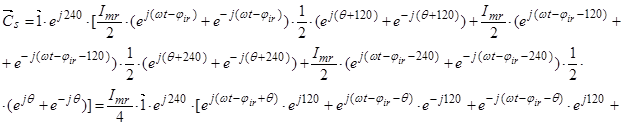
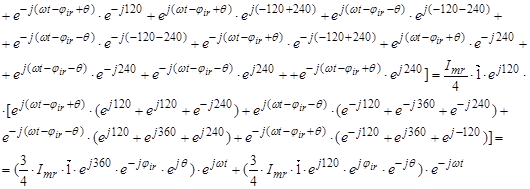

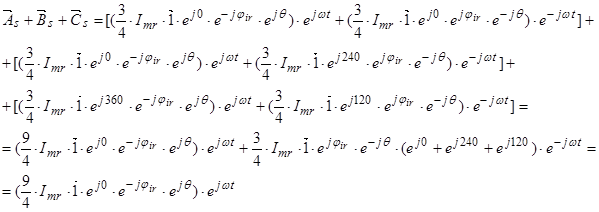
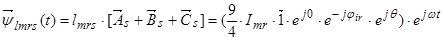
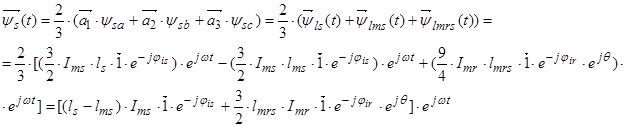 Обозначим
Обозначим 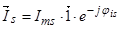 ;
; 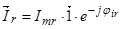 ;
; 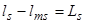 ;
; 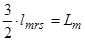 .
.
Окончательно, вектор потокосцепления статора[1] ÷ [3]:
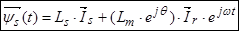 (14)
(14)
2. Вектор потокосцепления ротора АД
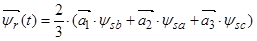 , (15)
, (15)
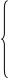
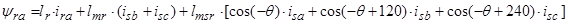
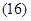
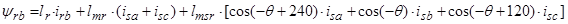
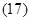
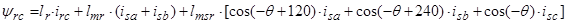
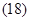
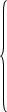
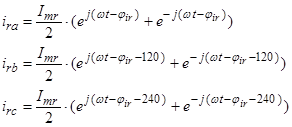
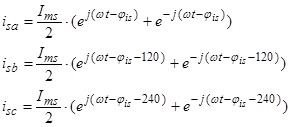
 Уравнения (16) ÷ (18) представим по трём столбцам соответствующих индуктивностей:
Уравнения (16) ÷ (18) представим по трём столбцам соответствующих индуктивностей:

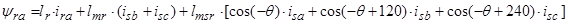
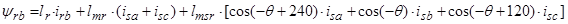
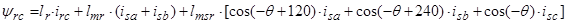
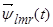
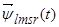
Первое уравнение умножим на 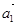 , второе – на
, второе – на 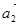 , третье – на
, третье – на 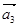 . Вначале произведем суммирование отдельно по вертикальным столбцам, а затем приведем полную сумму в соответствии с формулой (15).
. Вначале произведем суммирование отдельно по вертикальным столбцам, а затем приведем полную сумму в соответствии с формулой (15).
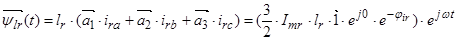
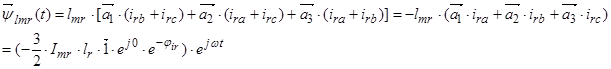
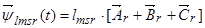 ,
,
где 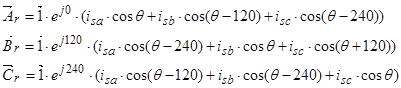
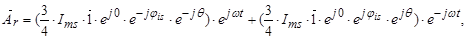
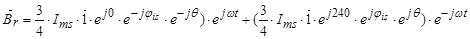
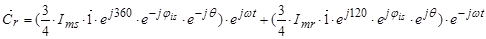
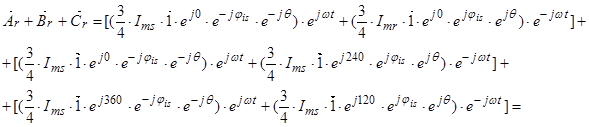
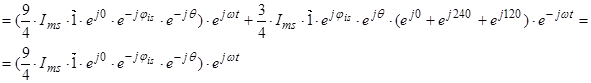
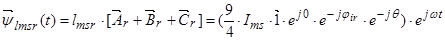
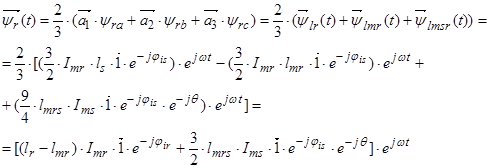
Обозначим 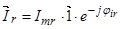 ;
; 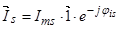 ;
; 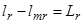 ;
; 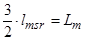 .
.
Окончательно, вектор потокосцепления ротора:
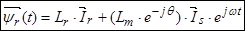 (19)
(19)
3. Векторные уравнения АД в различных системах координат
Основные уравнения асинхронного двигателя в векторной форме имеют вид:
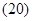
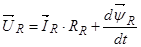
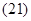
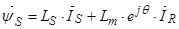
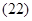
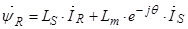
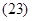
Сделаем существенное замечание по полученным обобщенным векторам. В уравнении (20) векторы 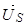 ,
, 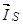 ,
, 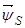 записаны в неподвижной системе координат статора, но в некоторых задачах их необходимо привести к системе координат связанных с ротором. Рассмотрим схему преобразования одного из векторов, например,
записаны в неподвижной системе координат статора, но в некоторых задачах их необходимо привести к системе координат связанных с ротором. Рассмотрим схему преобразования одного из векторов, например, 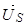 из одной системы координат в другую. Поясним это преобразование на следующем рис.2.
из одной системы координат в другую. Поясним это преобразование на следующем рис.2.
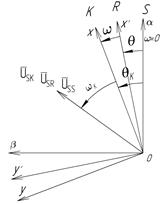
Рис.2. Система координат S, R, K.
 – неподвижная система координат статора
– неподвижная система координат статора 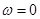 ;
; 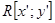 – система координат, связанная с ротором,
– система координат, связанная с ротором, 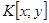 – произвольная система координат,
– произвольная система координат, 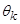 - угол сдвига к
- угол сдвига к 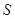 и
и 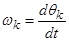 .
.
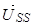 – обобщенный вращающийся вектор напряжения статора.
– обобщенный вращающийся вектор напряжения статора.
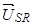 и
и 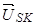 – этот же вращающийся вектор напряжения статора в системах координат ротора
– этот же вращающийся вектор напряжения статора в системах координат ротора 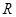 и
и 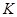 соответственно.
соответственно.
Связь между векторами в разных системах координат:
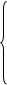
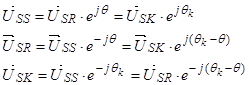
Система уравнений (20) – (23) примет следующий вид:
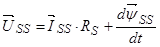 , (24)
, (24)
где 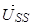 ,
, 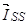 ,
, 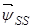 – записаны в не подвижной системе координат статора
– записаны в не подвижной системе координат статора  .
.
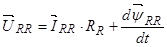 (25)
(25)
где  ,
, 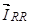 ,
, 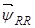 – обобщённые вектора роторных величин в роторной системе координат R.
– обобщённые вектора роторных величин в роторной системе координат R.
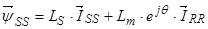 , (26)
, (26)
где 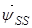 ,
, 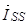 , – векторы потокосцепления и ток статора в неподвижной системе координат S, а
, – векторы потокосцепления и ток статора в неподвижной системе координат S, а 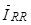 – в роторной системе координат сдвинутой в неподвижной системе на угол
– в роторной системе координат сдвинутой в неподвижной системе на угол  .
.
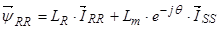 (27)
(27)
где 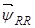 ,
, 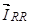 , – векторы потокосцепления и ток ротора в роторной системе координат R, а
, – векторы потокосцепления и ток ротора в роторной системе координат R, а 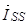 – в неподвижной системе координат
– в неподвижной системе координат 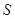 .
.
3.1 Рассмотрим приведение вышеприведённых уравнений к неподвижной системе координат статора
Уравнение (20) уже записано в статорной системе координат, поэтому показываем процесс приведения следующего уравнения. Для этого умножим обе части уравнение (21) на 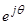 :
:
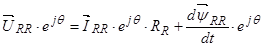 .
.
В соответствии с вышерассмотренной схемой приведения векторов из одной системы координат в другую, получим:
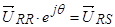 и
и 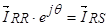 .
.
Выражение 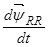 преобразуем к следующему виду:
преобразуем к следующему виду:
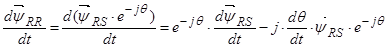
Окончательно 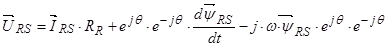 .
.
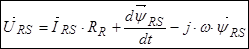 (28)
(28)
В выражении 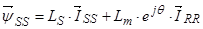 представим:
представим: 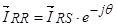 тогда
тогда
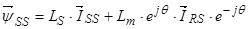
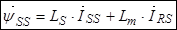 . (29)
. (29)
В уравнении (27) умножим обе части на 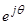 :
:
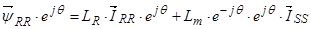 ,
,
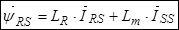 . (30)
. (30)
Окончательно уравнения (24) ÷ (27) в статорной системе координат примет следующий вид:
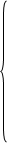
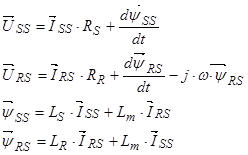
3.2 Выполним приведение уравнений (24) ÷ (27) к роторной системе координат
Умножим обе части уравнение (24) на 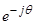 :
:
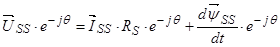
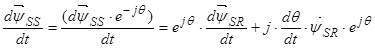
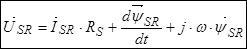
Уравнение (25) перепишем без изменений, т.к. оно уже записано в роторной системе координат:
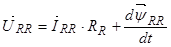
Уравнение (26) умножим обе части на 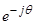 :
:
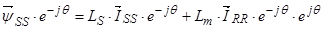 ,
,
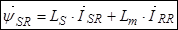
В уравнении (27) выразим 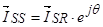 , тогда
, тогда
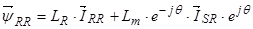 ,
,
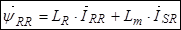
Окончательно в роторной системе координат уравнения (24) ÷ (27) имеют следующий вид:
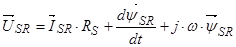
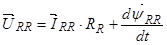
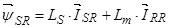
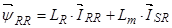
3.3 Приведение уравнений (24) ÷ (27) к системе координат вращающейся с произвольной скоростью 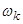
Уравнение (24) умножим на 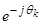 и сразу выразим
и сразу выразим 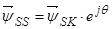 :
:
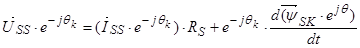 ,
,
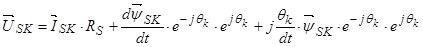 ,
,
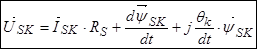 .
.
Уравнение (25) умножим на  :
:
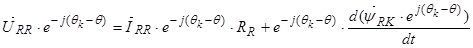 ,
,
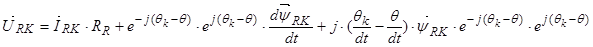
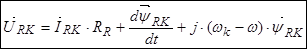 .
.
Уравнение (26) умножим на 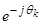 , тогда
, тогда
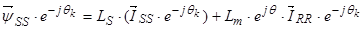 , т.к.
, т.к. 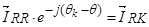 , то
, то
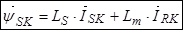 .
.
Уравнение (27) умножим на 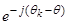 , тогда
, тогда
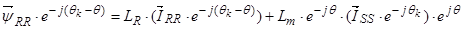
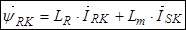 .
.
Для системы координат вращающейся с произвольной скоростью 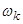 система уравнений:
система уравнений:
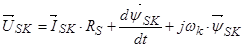 (31)
(31)
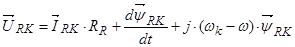 (32)
(32)
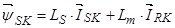 (33)
(33)
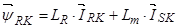 (34)
(34)
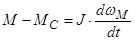 (35)
(35)
Зададим базовые величины (параметры):
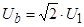 ;
; 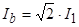 ;
; 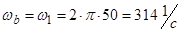 ,
,
где 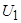 - номинальные действующее фазное напряжение двигателя;
- номинальные действующее фазное напряжение двигателя; 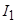 - номинальный фазный ток двигателя.
- номинальный фазный ток двигателя.
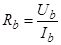 ;
; 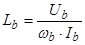 ;
; 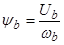 ;
; 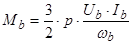 ;
;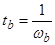 .
.
Обозначим относительные величины (параметры):
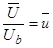 ;
;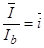 ;
; 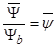 ;
; 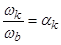 ;
; 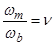 ;
; 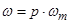 ,
,
где 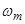 – механическая скорость вращения вала;
– механическая скорость вращения вала; 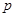 - число пар полюсов.
- число пар полюсов.
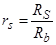 ;
; 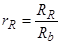 ;
; 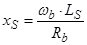 ;
;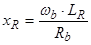 ;
; 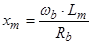 ;
; 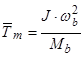 ;
; 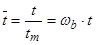
В уравнении (31) сделаем следующие преобразования, обе части разделим на 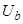 :
:
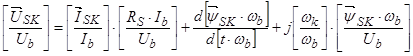 .
.
В квадратных скобках выделены соответствующие относительные величины.
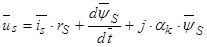
Аналогичные преобразования произведем в (32) уравнении:
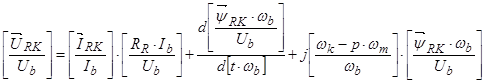 ,
,
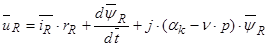
Для уравнения (33), умножим обе части уравнения на 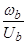 :
:
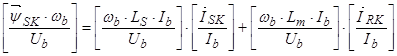 ,
,
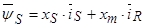
Аналогично в уравнении (34), умножим обе части на 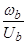 :
:
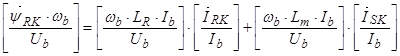 ,
,
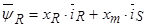
В уравнении (35) обе части разделим на 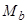 :
:
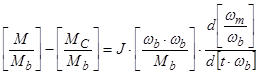 ,
,
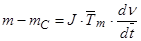
Система уравнения асинхронного двигателя с коротко замкнутым. ротором:
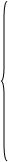
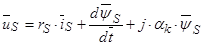 (36)
(36)
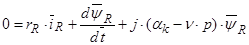 (37)
(37)
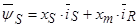 (38)
(38)
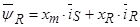 (39)
(39)
Определим электромагнитный момент через векторное произведение [1, c. 238]:
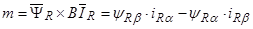
Выразим из уравнения (39) 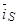 :
:
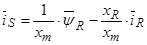
В уравнение (38) подставим 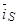 :
:
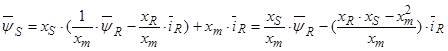
Обозначим 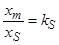 ,
, 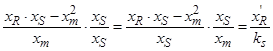 ,
, 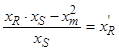 , тогда
, тогда
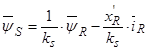 .
.
В уравнение (36) исключим 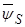 и
и 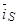 :
:
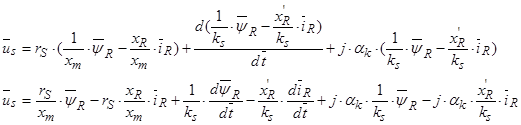
Из уравнения (37) выразим 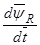 :
:
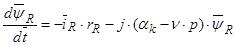 .
.
Подставим в предыдущее уравнение:
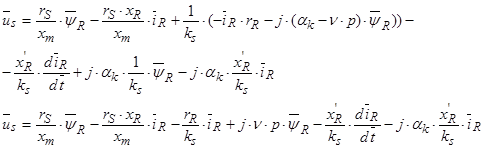
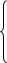
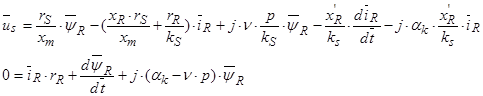
Обозначим 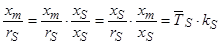 ,
, 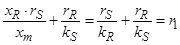 , где
, где 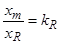 ,
, 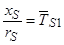
В итоге получилось два уравнения:
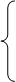
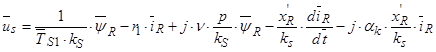 (40)
(40)
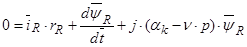 (41)
(41)
В уравнении (40) разделим обе части на 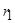 и обозначим
и обозначим 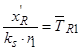 :
:
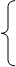
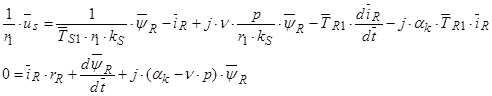
Рассмотрим процессы в неподвижной системе координат, 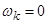 ,
, 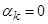 :
:
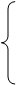
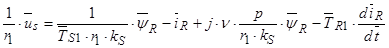 (42)
(42)
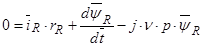 (43)
(43)
Вещественную ось обозначим 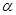 , мнимую через -
, мнимую через - 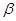 . Пространственные вектора в этом случае разложим по осям:
. Пространственные вектора в этом случае разложим по осям:
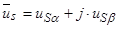 ;
; 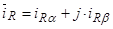 ;
; 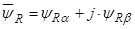 .
.
Подставим эти значения в уравнения (42) ÷ (43) и, приравняв отдельно вещественные и мнимые части, получим:
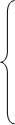
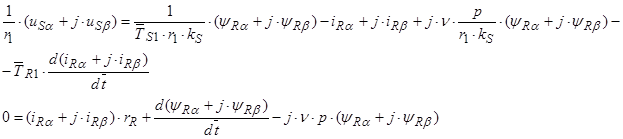
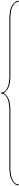
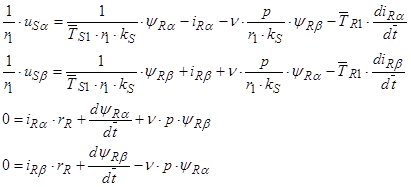
С учетом электромагнитных моментов [1, c. 238] система уравнений в операторной форме 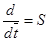 примет вид:
примет вид:
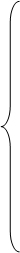
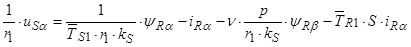 (44)
(44)
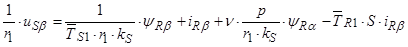 (45)
(45)
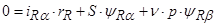 (46)
(46)
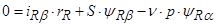 (47)
(47)
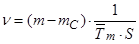 (48)
(48)
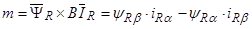 (49)
(49)
Структурная схема для уравнения(44):
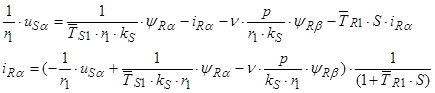
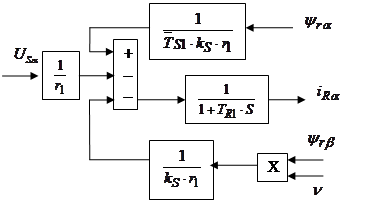

Структурная схема для уравнения(45):
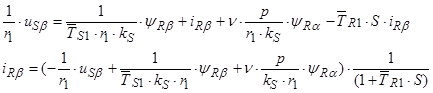
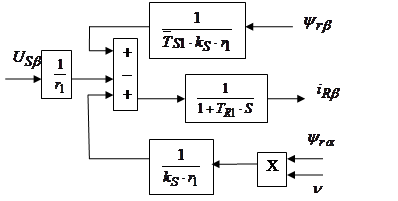

Структурная схема для уравнения(46):
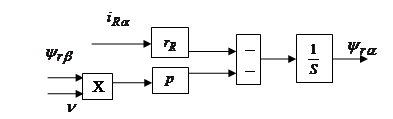
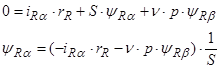

Структурная схема для уравнения(47):
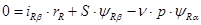
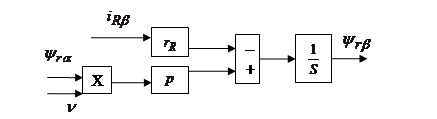
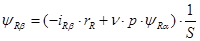

Структурная схема для уравнения (48):
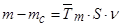
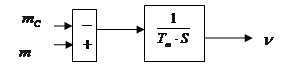

Структурная схема для уравнения (49):
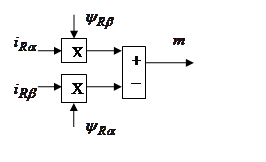
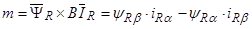

Для моделирования выберем АКЗ со следующими паспортными данными и параметрами: 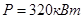 ,
, 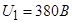 ,
, 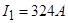 ,
, 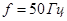 ,
, 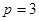 ,
, 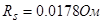 ,
, 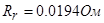 ,
, 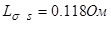 ,
, 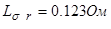 ,
, 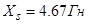 ,
, 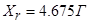 ,
, 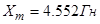 ,
, 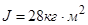 .
.
Значения безразмерных коэффициентов в уравнениях, рассчитанные по выражениям, приведенным выше:
|
Коэффициент |
|
|
|
|
|
|
|
|
|
Значение |
262.36 |
6.4 |
0.97 |
0.97 |
0.0152 |
0.0165 |
0.203 |
200 |
Модель АКЗ, построенная по уравнениям (44) ÷ (49), представленная на рис. 3.
На вход модели в момент времени 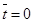 подаются напряжения
подаются напряжения 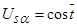 ,
, 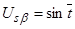 , (
, (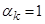 ), тем самым реализуя прямой пуск.
), тем самым реализуя прямой пуск.
Осциллоскопы измеряют относительные значения электромагнитного момента и скорости. Результаты моделирования представлены на рис. 4. Они показывают, что при прямом пуске вначале наблюдается значительные колебания момента. Такие же колебания наблюдаются в токе и скорости. Кроме того они показывают, что при приложении момента нагрузки наблюдается уменьшение скорости.
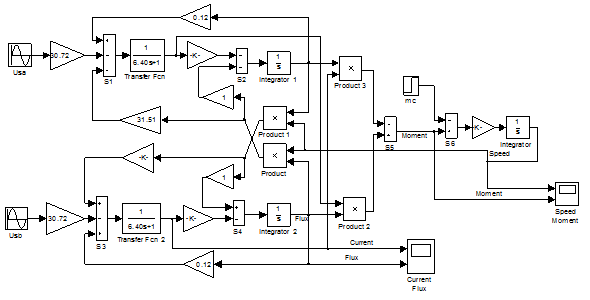
Рисунок 3. Модель АКЗ в неподвижной системе координат с переменными 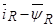
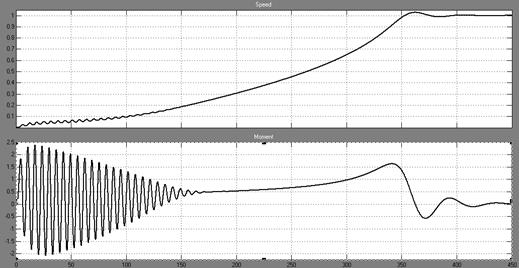
Рисунок 4. Результаты моделирования, относительные значения электромагнитного момента и скорости
Литература
1. Шрейнер Р.Т. Математическое моделирование электроприводов
переменного тока с полупроводниковыми преобразователями частоты. Екатеринбург: УРО РАН, 2000. 654 с.
2. Герман-Галкин С.Г. Компьютерное моделирование полупроводниковых систем Matlab 6.0: Учебное пособие. – Спб.: Корона принт. 2001. – 320с., ил.
3. Ковач К.П., Рац И. Переходные процессы в машинах переменного тока/Пер. с нем. М.Л.: Госэнергоиздат, 1963. 735 с.: ил.