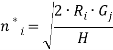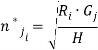Модели управления запасами применяются в области организации хранения и пополнения запаса соответствующего товара. Данная задача актуальна в торгово-посреднических компаниях. Если в рамках одной организации суммарная стоимость партии товара не вписывается в бюджет, то возникает конкуренция за ограниченный объем затрат. В этом случае встает задача определения ассортимента и оптимального распределения финансов. В условиях ограниченности складских помещений, партии различных товаров, поступивших на склад, могут не помещаться по объему. Здесь актуальной задачей становится оптимизация площади склада и распределения поставок по времени. Принятие грамотных управленческих решений способствует эффективному управлению складом, что снижает издержки хранения и доставки товара.
Единого критерия оптимизации логистических затрат не существует, поэтому стоит исходить из идеи минимизации группы наиболее значимых издержек хранения и доставки. В этом случае можно принять за условие минимизации соотношение входящих и исходящих финансовых потоков или обеспечение конкретных заказов потребителей. Решение таких задач способствуют развитию теории управления запасами, оптимизации подходов к выбору критериев и методов решения
Исследования в сфере распределения ресурсов часто сталкиваются с проблемами неопределенности и риска, причем значения ряда параметров модели и законы распределения вероятностей заданных величин зачастую неизвестны. Чаще всего элементы неопределенности и риска вносит случайный спрос на продукцию, изменение условий хранения и пополнения запасов, транспортные проблемы. В этих моделях оптимизация направлена на сбалансированность издержек, определение оптимального момента пополнения запаса и минимизацию общих потерь.
Известной математической моделью управления запасами является модель Уилсона, описывающая процесс закупки продукции у поставщика. Данная модель предусматривает изначально известные данные о количестве потребления продукции, затраты на ее хранение и доставку, а также время доставки. В свою очередь, помогая рассчитать оптимальный размер заказываемой продукции и размер запасаемой продукции, затраты на продукцию, периоды доставки. Основной формулой для модели Уилсона является:
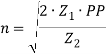
где ![]() размер заказа,
размер заказа,![]() –затраты при заказе,
–затраты при заказе, ![]() — потребление продукции,
— потребление продукции,![]() — затраты на хранение. После определения оптимального размера заказа определяют остальные характеристики, для которых служат исходными данными потребность в продукции, оптимальный размер заказа и время поставки продукции. Такие как уровень запаса в момент времени
— затраты на хранение. После определения оптимального размера заказа определяют остальные характеристики, для которых служат исходными данными потребность в продукции, оптимальный размер заказа и время поставки продукции. Такие как уровень запаса в момент времени ![]()
![]() (1)
(1)
где ![]() — начальный запас,
— начальный запас, ![]() — пополнение запасов,
— пополнение запасов, ![]() — расход, временной промежуток
— расход, временной промежуток ![]() .
.
Рассмотрим методы решения в условиях неопределенности для решения задачи оптимизации системы управления запасами, для которой параметры модели изначально не известны. Для начала рассмотрим основные понятия: годовое потребление продукции ![]() ; затраты на хранение за единицу продукции
; затраты на хранение за единицу продукции ![]() ; накладные расходы на одну поставку
; накладные расходы на одну поставку ![]() ; размер заказа
; размер заказа![]() ; цена закупки одной единицы товара
; цена закупки одной единицы товара ![]() ; цена реализации одной единицы товара
; цена реализации одной единицы товара ![]() ; общие годовые затраты
; общие годовые затраты ![]()
![]() (2)
(2)
общая годовая прибыль (до уплаты налогов)
![]() (3)
(3)
Задача максимизации общей годовой прибыли будет иметь вид:
![]() (4)
(4)
так как слагаемое ![]() не зависит от размера заказа
не зависит от размера заказа ![]() ) — оптимизируемого параметра, то задача сводится к задаче минимизации общих годовых затрат
) — оптимизируемого параметра, то задача сводится к задаче минимизации общих годовых затрат
![]() (5)
(5)
Получаем, что для оптимального размера заказа, при оптимизации прибыли и при всех известных параметрах модели
![]() (6)
(6)
где ![]() — размер заказа, оптимальный не только для минимизации общих годовых затрат, но и при достижении максимальной общей прибыли.
— размер заказа, оптимальный не только для минимизации общих годовых затрат, но и при достижении максимальной общей прибыли.
Обратим внимание, что показатели общих годовых затрат и прибыли включают в себя и специфические затраты, такие как, например, заработная плата и т. д. Однако, эти затраты не зависят от размера и периода поставки заказа, получаем, что они не будут влиять на выбор оптимального решения. Следовательно, этими данными можно пренебречь.
Затруднительным моментом задач в условиях неопределенности является то, что неизвестны значения некоторых параметров. В этом случае возможны оценки границ изменений соответствующих параметров в модели. В этом случае можно рассматривать в приделах границ различные возможности дальнейшего развития ситуации, которые будут влиять на саму задачу оптимизации.
Если есть условие на выбор разных поставщиков (для удобства будем считать что поставщиков двое), причем у каждого условия доставки могут быть свои. Учитывают, что потери прибыли так же различны и обусловлены претензиями к качеству продукции. Следовательно, выделены два варианта развития событий: благоприятный исход формирования прибыли, при низких показателях
1) Либо выбором вариантов для доли поставляемой продукции от рассматриваемых поставщиков,
2) Либо различными значениями для реализации величины годового потребления и значениями накладных расходов за поставку, зависящей от соответствующего обеспечения одним из поставщиков. В связи с тем, что доли распределения между поставщиками могут быль различными, то предположим, что претензии к качеству товара, только при закупке товара равными долями у обоих поставщиков. В этом случае, анализируемых решений будет шесть, данные представлены в таблице 1:
Таблица 1
Перечень анализируемых решений
|
Решение |
Условие |
Экономичный размер заказа |
|
|
Годовое потребление |
|
|
|
Годовое потребление |
|
где ![]()
Предположим, что цена реализации одной единицы продукции не зависит от выбора поставщика, в противном случае задачи оптимизации рассматриваются аналогично. Заметим так же, что увеличение размерности полезностей зависит от увеличения числа перераспределения долей поставляемой продукции между различными поставщиками.
Для дальнейших рассуждений потребуется матрица полезности, определим ее для показателей прибыли. Обычно строки матрицы — это анализируемые решения, а столбцы — случайные события. При заполнении матрицы для каждой ячейки потребуется определить величину ожидаемой годовой прибыли ![]() как элемента для решения
как элемента для решения ![]() и событием
и событием ![]() .
.
– ![]() — событие, когда годовое потребление низкое, низкая цена реализации, потери прибыли отсутствуют для обоих поставщиков.
— событие, когда годовое потребление низкое, низкая цена реализации, потери прибыли отсутствуют для обоих поставщиков.
– ![]() — событие, когда годовое потребление высокое, низкая цена реализации, потери прибыли отсутствуют для обоих поставщиков.
— событие, когда годовое потребление высокое, низкая цена реализации, потери прибыли отсутствуют для обоих поставщиков.
– ![]() — событие, когда годовое потребление низкое, высокая цена реализации, потери прибыли отсутствуют для обоих поставщиков.
— событие, когда годовое потребление низкое, высокая цена реализации, потери прибыли отсутствуют для обоих поставщиков.
–
– ![]() — событие, когда годовое потребление низкое, низкая цена реализации, потери прибыли для первого поставщика присутствует, а для второго поставщика отсутствует.
— событие, когда годовое потребление низкое, низкая цена реализации, потери прибыли для первого поставщика присутствует, а для второго поставщика отсутствует.
– ![]() — событие, когда годовое потребление высокое, низкая цена реализации, потери прибыли для первого поставщика присутствует, а для второго поставщика отсутствует.
— событие, когда годовое потребление высокое, низкая цена реализации, потери прибыли для первого поставщика присутствует, а для второго поставщика отсутствует.
– ![]() — событие, когда годовое потребление низкое, высокая цена реализации, потери прибыли для первого поставщика присутствует, а для второго поставщика отсутствует.
— событие, когда годовое потребление низкое, высокая цена реализации, потери прибыли для первого поставщика присутствует, а для второго поставщика отсутствует.
– ![]() — событие, когда годовое потребление высокое, высокая цена реализации, потери прибыли для первого поставщика присутствует, а для второго поставщика отсутствует.
— событие, когда годовое потребление высокое, высокая цена реализации, потери прибыли для первого поставщика присутствует, а для второго поставщика отсутствует.
– ![]() — событие, когда годовое потребление низкое, низкая цена реализации, потери прибыли для первого поставщика отсутствует, а для второго поставщика присутствует.
— событие, когда годовое потребление низкое, низкая цена реализации, потери прибыли для первого поставщика отсутствует, а для второго поставщика присутствует.
– ![]() — событие, когда годовое потребление высокое, низкая цена реализации, потери прибыли для первого поставщика отсутствует, а для второго поставщика присутствует.
— событие, когда годовое потребление высокое, низкая цена реализации, потери прибыли для первого поставщика отсутствует, а для второго поставщика присутствует.
– ![]() — событие, когда годовое потребление низкое, высокая цена реализации, потери прибыли для первого поставщика отсутствует, а для второго поставщика присутствует.
— событие, когда годовое потребление низкое, высокая цена реализации, потери прибыли для первого поставщика отсутствует, а для второго поставщика присутствует.
– ![]() — событие, когда годовое потребление высокое, высокая цена реализации, потери прибыли для первого поставщика отсутствует, а для второго поставщика присутствует.
— событие, когда годовое потребление высокое, высокая цена реализации, потери прибыли для первого поставщика отсутствует, а для второго поставщика присутствует.
– ![]() — событие, когда годовое потребление низкое, низкая цена реализации, потери прибыли для обоих поставщиков присутствует.
— событие, когда годовое потребление низкое, низкая цена реализации, потери прибыли для обоих поставщиков присутствует.
– ![]() — событие, когда годовое потребление высокое, низкая цена реализации, потери прибыли для обоих поставщиков присутствует.
— событие, когда годовое потребление высокое, низкая цена реализации, потери прибыли для обоих поставщиков присутствует.
–
– ![]() — событие, когда годовое потребление высокое, высокая цена реализации, потери прибыли для обоих поставщиков присутствует.
— событие, когда годовое потребление высокое, высокая цена реализации, потери прибыли для обоих поставщиков присутствует.
Выведем формулы для соответствующих расчетов элементов матрицы в первом столбце. Для этого используем формулу 3. Но заметим, что: параметры ![]() — не зависит от выбора элемента, так как задан,
— не зависит от выбора элемента, так как задан, ![]() определяются для каждого решения, а
определяются для каждого решения, а ![]() определяются для каждого события, не зависимо от решения.
определяются для каждого события, не зависимо от решения.
Рассмотрим формулы величин ожидаемой годовой прибыли на примере первого столбца. При наступлении события ![]() при котором условия
при котором условия
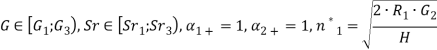
Для оставшихся параметров получаем, что годовая прибыль будет рассчитываться следующим образом:
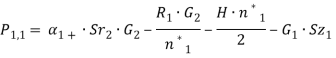 (7)
(7)
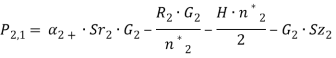 (8)
(8)
![]() (9)
(9)
где
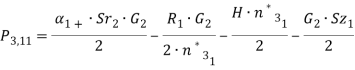
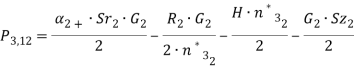
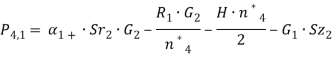 (10)
(10)
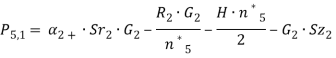 (11)
(11)
![]() (12)
(12)
где
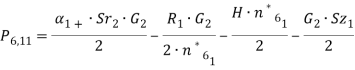
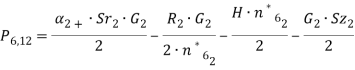
1) Выпишем условия, какие будут меняться для следующего столбца в таблице 2:
Таблица 2
Изменение условий в событиях.
|
Событие |
Изменение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для нахождения оптимального решения в условиях неопределенности еще требуется выбрать альтернативное решение с учетом конкретного критерия. Критерии объединяют в следующие группы: классические критерии и производственные критерии. Для выбора критерия нужно обращать внимание на: специфику соответствующего аппарата «линий уровня» используемого критерия, специфику непосредственно рассматриваемой задачи оптимизации, и специфику индивидуальных требований. На практике, большое внимание уделяется выбору критерия для оптимизации решения. Его выбор зависит от того, насколько серьезный подход к решению сложившейся ситуации. Рассмотрим некоторые из них.
Начнем с ММ-критерия. Критерий предполагает, что будет введена одна дополнительная строка в матрице полезности. Ее элементами по столбцам будут заполнены самыми плохими показателями, затем из всех значений в строке выберется наибольшее — это и будет оптимальное решение.
ММ-критерий:
![]() (13)
(13)
ММ-Критерий обеспечивает лучший гарантийный результат по отношению к худшему варианту развития событий, однако при нем возможны потери в прибыли относительно ко многим возможным реализациям при других решениях.
Другим критерием выступает Н-критерий. Отличительная особенность этого критерия от ММ-критерия состоит в том, что в заполнении дополнительной строки, элементы выбираются самыми лучшими из всех значений выбирается максимальный, который принимается как наилучшее решение.
Н-критерий:
![]() (14)
(14)
Н-Критерий обеспечивает максимальную прибыль, однако реализация такого вывода предполагает, что реализована только наиболее благоприятное событие из всей группы. Один из минусов состоит в том, что есть возможность значительно потерять размер прибыли при неблагоприятной реализации в случае ко многим событиям при других решениях.
Следующим критерием рассмотрим критерий Гурвица. Отличимым от предыдущих критериев тем, что элементы в дополнительной строке заполнены средними арифметическими взвешенными значениями для показателей обоих предыдущих критериев. Из всех полученных значений выбирается максимальное, а его решение выбирается, как наилучшее в рамках данного критерия к риску отклонения результата на основе выбранного значения параметра.
Критерий Гурвица:
![]() (15)
(15)
где ![]() — весовой коэффициент. Заметим, что выбор весового коэффициента выбирается непосредственно для конкретного случая самим человеком.
— весовой коэффициент. Заметим, что выбор весового коэффициента выбирается непосредственно для конкретного случая самим человеком.
Была рассмотрена модель со следующими условиями: при годовой потребности в продукции 2008 шт., число рабочих дней в году 242 дней, оптимальный размер заказа составил 79 шт., время поставки 7 дней, возможная задержка поставки 2 дня.
В результате получены значение всех уровней запаса, которые показывают количество продукции, находящейся в магазине показанные на рисунке 1.
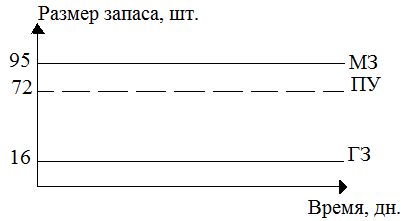
Рис. 1. Размеры запасов
Добавляя условия на двух поставщиков. Потребуется дополнить данные. Годовые затраты за ранение единицы продукции ![]() , руб; Накладные расходы на поставку у первого поставщика
, руб; Накладные расходы на поставку у первого поставщика![]() , руб, у второго поставщика
, руб, у второго поставщика![]() , руб.; Цена закупки единицы товара у первого поставщика
, руб.; Цена закупки единицы товара у первого поставщика ![]() , руб, у второго поставщика
, руб, у второго поставщика ![]() , руб; Понижающий коэффициент, для выручки при благоприятной реализации продукции первого поставщика,
, руб; Понижающий коэффициент, для выручки при благоприятной реализации продукции первого поставщика, ![]() , у второго поставщика,
, у второго поставщика, ![]() ; Понижающий коэффициент, для выручки при неблагоприятной реализации продукции первого поставщика,
; Понижающий коэффициент, для выручки при неблагоприятной реализации продукции первого поставщика, ![]() у второго поставщика,
у второго поставщика, ![]() .
.
В результате чего получены решения для двух поставщиков с учетом годового потребления.
![]()
![]()
Получены значения для размеров заказа соответствуют всем возможным ситуациям в работе с поставщиками. Затем получены значения прибыли и убытков по критерию Гурвица, для различных значениях весового коэффициента, в таблице 3:
Таблица 3
Критерий Гурвица
|
Критерий Гурвица |
Решение |
|||||
|
|
|
|
|
|
|
|
|
ММ-критерий |
-28463 |
-499651 |
-191652 |
-22372 |
-333830 |
-180699 |
|
Н-критерий |
595938 |
546905 |
22288 |
-14675 |
92304 |
33241 |
|
K=0 |
595938 |
546905 |
22288 |
-14675 |
92304 |
33241 |
|
K=0,1 |
533498 |
442249 |
894 |
-15445 |
49691 |
11847 |
|
K=0,2 |
471058 |
337594 |
-20500 |
-16214 |
7077 |
-9547 |
|
K=0,3 |
408618 |
232938 |
-41894 |
-16984 |
-35536 |
-30941 |
|
K=0,4 |
346178 |
128283 |
-63288 |
-17754 |
-78150 |
-52335 |
|
K=0,5 |
283738 |
23627 |
-84682 |
-18524 |
-120763 |
-73729 |
|
K=0,6 |
221297 |
-81029 |
-106076 |
-19293 |
-163376 |
-95123 |
|
K=0,7 |
158857 |
-185684 |
-127470 |
-20063 |
-205990 |
-116517 |
|
K=0,8 |
96417 |
-290340 |
-148864 |
-20833 |
-248603 |
-137911 |
|
K=0,9 |
33977 |
-394995 |
-170258 |
-21602 |
-291217 |
-159305 |
|
K=1 |
-28463 |
-499651 |
-191652 |
-22372 |
-333830 |
-180699 |
В результате чего наблюдалась статистика повышения, либо понижение прибыли. Для первого решения, прибыль с повышением коэффициента понижается и доходит до состояния убытка. Для 2–6 решения, прибыль с повышением коэффициента понижается, а размер убытка увеличивается. Такой выбор работы с поставщиками негативно будет сказывается на работу магазина. Что будет гарантировать закрытие магазина. Следовательно, магазин будет иметь прибыль только в одном из всех полученных случаев, при поставках от первого поставщика. Это говорит о том, что при рассматриваемых условиях работа с первым поставщиком более надежна и выгодна в отличии от второго.
Критерий Гурвица удобен тем, что показывает размер прибыли и убытков магазина. Так как выбор весового коэффициента зависит не только от самого магазина, но и от надежности поставщиков. Получаем второе преимущество данного метода: возможность изучить состояние в магазине для различных значений весового коэффициента и проанализировать ситуацию работы с конкретными поставщиками. Что касается других критериев, они дают однозначный ответ только о финансовом состоянии магазина, что удобно для неглубокого изучения статистики прибыли/убытков магазина.
Литература:
- Толмачев О. В. «Логистика товародвижения» Екатеринбург, УрФУ, 2013, 361 стр.
- Шнуриков П. В., Иванов А. В. «Исследование задачи оптимизации в дискретной полумарковской модели управления непрерывным запасом» М., Вестник МГТУ им. Н. Э. Баумана № 3, 2013, 62–87 стр.
- Библя Г. Н. «Оптимизация стратегии управления деятельностью it-компании на основе методов нечеткой логики», Вестник ИМСИТ № 3 (67), 2016, С. 57–59.
- Кремер Н. Ш. «Исследование операций в экономике» М., ЮНИТИ, 2003, 407 стр.
- Бродецкий Г. Л. «Системный анализ в логистике. Выбор в условиях неопределенности» М., Academia, 2010, 336 стр.
- Библя Г. Н., Ермолаева А. А. «Методы выбора оптимальных каналов доставки товаров», М, Сборник статей по материалам III международной заочной научно-практической конференции, 2017, С. 44–50.
- Аникина Б. А. «Практикум по логистике» М., ИНФРА-М, 2006, 276 стр.