Улучшение качества рентгеновских цифровых изображений можно производить как с помощью линейных преобразований [1], так и с помощью фильтрации в частотной области после выполнения преобразования Фурье. Находясь в основе методов линейной фильтрации, преобразование Фурье обеспечивает значительную гибкость при разработке и реализации алгоритмов фильтрации при решении задач улучшения, восстановления и сжатия изображений.
Основные шаги фильтрации в частотной области. Через f обозначим исходное изображение, а через g — результат фильтрации. Предполагается, что передаточная функция H(u,v) имеет те же размеры, что и исходное изображение.
- Получить параметры расширения с помощью paddedsize: PQ = paddedsize (size(f));
- Построить преобразование Фурье с расширением: F = fft2(f, PQ(1), PQ(2));
- Сгенерировать функцию фильтра Н размера PQ(l)xPQ(2) одним из описываемых далее методов. Если он был центрирован, до использования его в фильтрации следует выполнить команду Н = fftshift(H).
- Умножить преобразование Фурье на передаточную функцию фильтра: G = H*F;
- Найти вещественную часть обратного преобразования Фурье от G: g = real(ifft2(G));
- Вырезать верхний левый прямоугольник исходных размеров:
g = g(l:size(f,1), l:size(f,2));
Эта процедура фильтрации схематически изображена на рис. 1. Предварительная стадия обработки может состоять из определения размеров изображения, вычисления параметров расширения и генерации фильтра. Заключительная стадия обработки состоит в выделении вещественной части результата, обрезания изображения до исходного размера и его конвертации в класс uint8 или uintl6 для сохранения на диске.
Передаточная функция фильтра Н(u, v) на рис. 1 умножается на вещественную и мнимую части F(u, v). Если функция Н(u, v) была вещественной, то фазовая часть произведения не меняется, что видно из фазового уравнения, так как при умножении вещественной и мнимой части комплексного числа на одно и то же вещественное число фазовый угол не меняется. Такие фильтры принято называть фильтрами с нулевым сдвигом фазы.
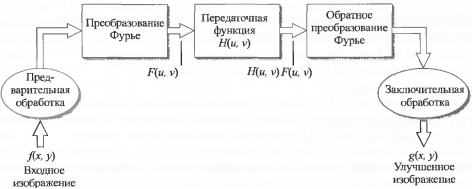
Рис. 1. Основные шаги фильтрации в частотной области
Последовательность описанных выше шагов фильтрации используется в этой главе и в части следующей, поэтому удобно иметь М-функцию, аргументами которой являются изображение и передаточная функция фильтра, которая выполняет все необходимые процедуры фильтрации и возвращает отфильтрованное и обрезанное изображение. Следующая функция как раз совершает все эти действия.
function g = dftfilt(f, H)
G = DFTFILT(F,H)
F = fft2(f, size(H, 1), size(H, 2))
g = real(ifft2(H.*F));
Crop to original size.
g = g(1:size(f, 1), 1:size(f, 2));
g = mat2gray(g);
В следующих М-функциях важную роль играет процедура вычисления расстояния между любыми точками частотного прямоугольника. Поскольку в MATLAB при выполнении FFT предполагается, что начало отсчета находится в верхнем левом углу частотного прямоугольника, вычисления расстояния ведутся от этой точки. Для лучшей визуализации центр данных можно смещать функцией fftshift.
Следующая функция dftuv создает сеточный массив, который используется при вычислении расстояний и при других подобных действиях.
function [U,V]=dftuv(M,N)
[U,V] = DFTUV(M,N) u = 0:(M-1);
v = 0:(N-1);
idx = find(u > M/2);
u(idx) = u(idx)-M;
idy = find(v > N/2);
v(idy) = v(idy)-N;
Compute the meshgrid arrays.
[V, U] = meshgrid(v, u);
Следующая программа генерирует передаточные функции низкочастотных фильтров, которые выделяют основное содержание изображения — фон и крупноразмерные объекты.
function [H,D] = lpfilter(type,M,N,D0,n)
H = LPFILTER (TYPE,M,N,D0,n) [U, V] = dftuv(M, N);
Compute the distances D(U, V) .
D = sqrt(U.^2 + V.^2);
H = double(D <= D0); case 'btw'
if nargin == 4 n = 1;
end
H = l./(l + (D./D0).^(2*n));
case 'gaussian'
H = exp((D.^2)./(2*(D0^2)));
otherwise
error('Unknown filter type.')
end
Имея передаточную функцию ![]() низкочастотного фильтра, можно подучить передаточную функцию соответствующего высокочастотного фильтра с помощью формулы
низкочастотного фильтра, можно подучить передаточную функцию соответствующего высокочастотного фильтра с помощью формулы
![]() .
.
Значит, функцию lpfilter, разработанную для низкочастотного фильтра, можно использовать для построения генератора высокочастотных фильтров:
function H = hpfilter(type, M, N, D0, n)
H = HPF ILTER (TYPE, M, N, DO, n)
if nargin == 4
n = 1; Default value of n.
end
Generate highpass filter.
Hlp = lpfilter(type, M, N, D0, n);
H = 1-Hlp.
Наилучший результат при обработке затемненных рентгеновских изображений даёт комбинация высокочастотной фильтрации с последующей гистограммной эквализацией. Команды MATLAB, реализующие эти действия при помощи разработанных выше фильтров:
PQ = paddedsize(size(f));
D0 = 0.05*PQ(1);
HBW = hpfilter('btw', PQ(1), PQ(2), D0, 2);
H = 0.5 + 2*HBW;
gbw = dftfilt(f, HBW);
gbw = gscale(gbw);
ghf = dftfilt(f, H);
gbf = gscale(ghf);
ghe = histeq(gbf, 256);
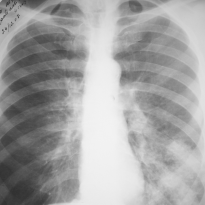
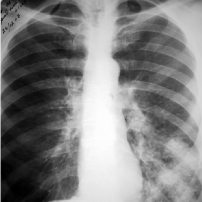
Результат фильтрации с усилением высоких частот приведён на рис. 2.
а) б)
Рис. 2. Рентгеновское изображение: а) — исходное, б) после фильтрации с усилением высоких частот
Основная сфера применения фильтрации с усилением высоких частот в задачах обработки биомедицинских изображений является повышение резкости рентгенографических изображений. Рентгеновские лучи не могут быть сфокусированы с помощью линз, как световые лучи, поэтому большинство рентгеновских снимков выглядят расплывчато. Зачастую яркость рентгенографических изображений сдвинута в темную область, поэтому также необходимо использовать методы обработки изображения для увеличения яркости контрастности изображения. Фильтрация с усилением высоких частот делает снимок более контрастным и повышает четкость.
Литература:
- Куликов А. Ю., Строев В. М., Есаулова К. А., Долгова Ю. Н. Обработка рентгеновских изображений с применением оценки качества и выбора оптимальных параметров коррекции // Молодой ученый. — 2017. — № 12. — С. 63–66.
- Методы компьютерной обработки биомедицинских изображений в среде MATLAB: учеб. пособие / А. А. Федотов, С. А. Акулов, А. С. Акулова. — Самара: Изд-во СГАУ, 2015. — 88 с.

