Ключевые слова: задача линейного программирования, многокритериальная оптимизация, метод последовательных уступок
Метод последовательных уступок решения многокритериальных задач применяется в случае, когда частные критерии могут быть упорядочены в порядке убывающей важности. Предположим, что все критерии максимизируются и пронумерованы в порядке убывания их важности. Сначала определяется максимальное значение ![]() , первого по важности критерия в области допустимых решений, решив задачу
, первого по важности критерия в области допустимых решений, решив задачу ![]() , при
, при ![]() . Затем назначается, исходя из практических соображений и принятой точности, величина допустимого отклонения
. Затем назначается, исходя из практических соображений и принятой точности, величина допустимого отклонения ![]() (уступка) критерия
(уступка) критерия ![]() и отыскивается максимальное значение критерия
и отыскивается максимальное значение критерия ![]() при условии, что значение первого должно отклоняться от максимального не более чем на величину допустимой уступки, то есть решается задача:
при условии, что значение первого должно отклоняться от максимального не более чем на величину допустимой уступки, то есть решается задача:
![]()
Снова назначается величина уступки ![]() по второму критерию, которая вместе с первой используется при нахождении условного экстремума третьего частного критерия и т. д. Наконец, выявляется экстремальное значение последнего по важности критерия
по второму критерию, которая вместе с первой используется при нахождении условного экстремума третьего частного критерия и т. д. Наконец, выявляется экстремальное значение последнего по важности критерия ![]() при условии, что значение каждого из первых
при условии, что значение каждого из первых ![]() частных критериев отличается от экстремального не более, чем на величину допустимой уступки. Получаемое на последнем этапе решение считается оптимальным. Средствами MatLab была разработана программа, позволяющая решать данные задачи любой размерности. Рассмотрим работу алгоритма на примере. Пусть даны:
частных критериев отличается от экстремального не более, чем на величину допустимой уступки. Получаемое на последнем этапе решение считается оптимальным. Средствами MatLab была разработана программа, позволяющая решать данные задачи любой размерности. Рассмотрим работу алгоритма на примере. Пусть даны:
![]()
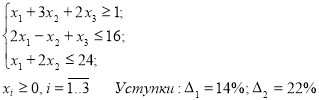
Алгоритм основан на встроенной функции MatLab для решения задач линейного программирования — linprog. На вход программе подаются следующие значения:
FN — количество переменных задачи; FM — количество ограничений задачи; FF — количество целевых функций; US — вектор уступок; AF — матрица коэффициентов при переменных целевых функций; GF — вектор направлений ЦФ; OG — матрица коэффициентов при переменных ограничений; SO — вектор знаков ограничений; OF — вектор свободных коэффициентов ограничений:
FN = 3; FM = 3; FF = 3; AF = [2 1 -3; 1 3 -2; -1 2 4];
GF = [1 0 1]; US = [14 22]; OG = [1 3 2; 2 -1 1; 1 2 0];
SO = [1 0 0]; OF = [1 16 24];
Далее введённые данные адаптируются под синтаксис процедуры linprog (ограничения сводятся к «≤», ЦФ сводятся на max, путём домножения на -1 ЦФ, направленных на min) и выполняется непосредственный поиск решения:
%Настройка функции linprog на решение симплекс-методом
options = optimset('LargeScale', 'off','Simplex','on');
%Поиск решения текущей ЦФ — tAF (выбираются строки из AF)
[x,fval]=linprog(tAF,OG,OF, [], [],lb, [], [],options).
Производим поиск решения столько раз, сколько имеем ЦФ (FF). Функция linprog возвращает вектор значений для целевой функции Х и fval — значение ЦФ при таких X. Добавляем каждый найденный вектор решения в матрицу решений FS, добавляя полученное решение в качестве дополнительного ограничения.
Рассчитываем значение найденной ЦФ с учетом уступок. Выведем полученное решение, «распечатав» FS(i), FS(i)*US(i), x(i), где i = 1...FF, а также решение с учетом уступок (Рис. 1, 2).
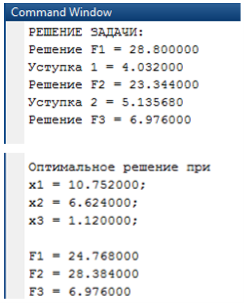
Рис. 1. Оптимальное решение задачи
Таким образом, в среде программирования MatLab (R2015b) был разработан алгоритм, позволяющий решать задачи многокритериального линейного программирования методом последовательных уступок. Данный код универсален для любых размерностей: любого числа целевых функций, числа переменных и ограничений.
Литература:
- Штойер Р. Многокритериальная оптимизация / Штойер Р.: пер. с англ. — М.: Радио и связь, 1992. — 504 с. — (Теория, вычисления и приложения).

