Ключевые слова: топологическая оптимизация, Python
Топологическая оптимизация стала хорошо зарекомендовавшей себя технологией, применяемой инженерами во многих областях промышленности. С точки зрения постановки задачи, топологическая оптимизация может описываться как процесс определения оптимального распределения ограниченного материала в области проектирования, для выполнения некоторой предопределенной функции. Задача моделируется в виде задачи нелинейного программирования, решение которого можно получить разными эффективными методами нелинейного программирования [1]. TOPY базируется на открытом для всех разработчиков языке Python, а сам исходный код TOPY защищается лицензией MIT License, что позволяет любому разработчику без ограничений использовать данное решения как для научных, так и для коммерческих целей. Актуальность TOPY обоснована доступностью для любого разработчика исходного кода, а также относительной легкостью в изучении Python так как он похож на используемый многими инженерами язык Matlab
Конечная цель состоит в получении результата, состоящего преимущественно или даже частично из дискретных твердотельных областей в пределах исходной области проектирования удовлетворяемая поставленным задачам. В простейшем случае (математическая) оптимизация — это процесс нахождения экстремума целевой функции в некоторой области конечномерного пространства, ограниченной набором линейных или не линейных неравенств.
Архитектура TOPY представлена на Рис. 1, показаны лишь основная структура пакета.
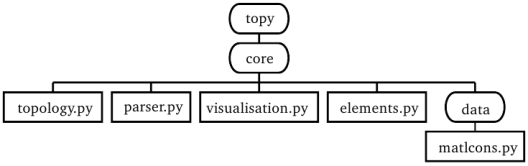
Рис. 1. Архитектура TOPY
Для описания проблемы оптимизации топологии создается файл, который анализируется, такой файл именуется файлом определения задачи, который обрабатывается модулем “parser.py”, модуль “topology.py” используется для визуализации хода оптимизации, в модуле “topology.py” реализуется экспоненциальная и диагональная аппроксимация, а также фильтр серого цвета с диагональной квадратичной аппроксимацией [3, с. 48], модуль “elements.py” описывает конечно-элементную сетку создаваемую для решаемой задачи.
Для использования TOPY необходима версия Python не выше 2.7.x, наличие установленных библиотек “ NumPy+MKL”, “ PySparse”, “ PyVTK”, “matplotlib”, “ SymPy”, после установки этих пакетов необходимо установить сам TOPY, запуск оптимизации осуществляется посредством передачи “ optimise.py” пути на файл определения задачи с расширением “.tpd” пример команды: “python optimise.py *.tpd”, после запуска ход оптимизации будет отображается в консоли (Рис. 2)
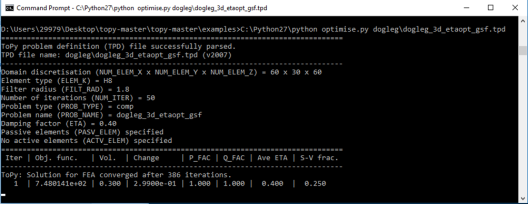
Рис. 2. Процесс выполнения файла с заданием
Результат выполнения на каждой итерации будет хранится в том-же каталоге откуда производится запуск, в папке “Steps” (Рис. 4), для 2d заданий TOPY будет сохранять в каталоге изображения с разрешением пропорциональным сетке задания, при выполнении 3d заданий TOPY будет сохранять результат работы в файлах с расширением “.tpk” которые не представляет труда открыть программе PARAVIEW (Рис. 5).
Для описания задания используется специальный синтаксис, давайте рассмотрим на примере нагруженной балки (нагрузка изображена красной стрелкой) (Рис. 3)
Файл с заданием для этого примера имеет следующий вид:
[ToPy Problem Definition File v2007]
# Author: William Hunter
# The 'classic' 60x20 2d mbb beam, as per Ole Sigmund's 99 line code.
PROB_TYPE : comp
PROB_NAME : beam_2d_reci
ETA : 0.5 # reciprocal approx.
DOF_PN : 2
VOL_FRAC : 0.5
FILT_RAD : 1.5
ELEM_K : Q4
NUM_ELEM_X : 60
NUM_ELEM_Y : 20
NUM_ELEM_Z : 0
FXTR_NODE_X: 1|21
FXTR_NODE_Y: 1281
LOAD_NODE_Y: 1
LOAD_VALU_Y: -1
NUM_ITER : 250
P_FAC : 3
где:
PROB_TYPE — Тип проблемы;
PROB_NAME — Имя проблемы;
ETA — Отвечает за степень округления при каждой итерации;
DOF_PN — Количество степеней свободы для ноды;
VOL_FRAC — Объемная доля твердого материала к общему объему доменов;
FILT_RAD — Радиус действия фильтра;
ELEM_K — Матрица жесткости элемента;
NUM_ELEM_X — Количество элементов по соответствующей оси;
FXTR_NODE_X — Параметры жёсткости ноды;
LOAD_NODE_Y — Номер нагружаемой ноды;
LOAD_VALU_Y — Значение нагружаемой силы;
NUM_ITER — Число выполняемых итераций;
P_FAC — Штрафной фактор.
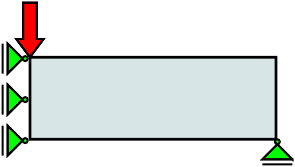
Рис. 3. 2d нагруженная балка

Рис. 4. Графическое представление процесса выполнения 2d задания оптимизации на каждой итерации
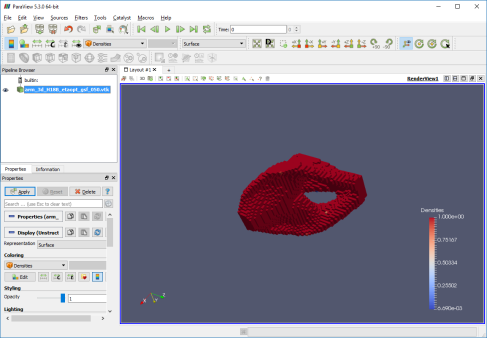
Рис. 5. Графическое представление процесса выполнения 3d задания оптимизации
TOPY может применятся в академических целях для наглядного изучения вопросов связанных с топологической оптимизацией, так как исходный код доступен для всех желающих.
Литература:
- Betts J. T. Methods of Optimal Control and Estimation Using Nonlionear Programming. 2nd ed. Philadelphia.: SIAM, 2010, 434 p.
- Ричард Столлман. X11 License (англ.). Various Licenses and Comments about Them. Доступно: http://www.gnu.org/licenses/license-list.html#X11License
- Hunter, William. Predominantly solid-void three-dimensional topology optimisation using open source software. University of Stellenbosch, 2009.

