Definition of probabilistic characteristics of stress



In deterministic calculations the strength of the structural elements is estimated by safety factor n = R / S, where R is the ultimate stress of the material, and S is rated stress. If the stresses are random values, the performance of structural elements should be evaluated by reliability, interpreted as the probability of not exceeding the operating stress. For that it is necessary to know the probabilistic characteristics of the stresses.

For elastic systems the maximum stresses in the dangerous section of S in general form can be written as:

,(1)

where q — the generalized parameter having a load sense;

k — coefficient depending on the geometrical design parameters.

The specific form of these parameters, we obtain in solving the determined problem of strained-deformed state of the construction. Thus, in the course of the resistance of materials q is an internal power factor, and the coefficient K is one of the geometric characteristics of the cross-section: with tension and compression, it is equal to the square, with torsion and bend it is equal to the corresponding resistance moments. Internal power factor can be expressed through external loads by section method.

Let the random load with a known distribution law P (q) acts on the construction. Then the maximum stress distribution law can be found from the formula of probability transformation.

.(2)

With this transformation the stresses and loads distribution laws coincide, and only the parameters of the distribution are changed. So, they are converted to the normal distribution as follows:

m_s=m_q/k, _s=_q/k,

where m, — the expectation of a random value standard.

If the design has several accidental loads qi, then the generalized load parameter is a linear combination of random values.

If the load of qi, have a normal distribution, then q also has a normal distribution with parameters defined by the formula

where the variance of the random value D=σ², a k_ij=<(q_i-m_qi)(q_j-m_qj)>.

For non-correlated random value sk_ii = 0.

In general, the distribution density f (q) is found by determining the function density distribution law from several random arguments

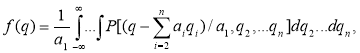
Where p(q₁, … q_n)) — a joint density of random values distribution q_i. If the random loads are not correlated, this formula takes the form

(3)

Where Рi(qi) — the distribution density of the random value q_i.

In the latter case, one can be used the principle of superposition and write

where the density of random values distribution Si is determined by the formula (2). Now one can be used the expression (3) to determine the maximum stresses distribution density.

Now consider the case where, with the load the parameters of geometric designs are random in this case, in the formula (1) the random parameter is k. From the physical meaning of the parameters follows that the random values q and k are uncorrelated. Then their joint distribution density is

where P (k) — the density of the parameter distribution.

Now, on the probabilities conversion formula the law of distribution maximum stresses can be found

.(4)

The parameter is usually a power function from the cross-section size. Due to physical reasons the sectional size often is a random value distributed according to the normal law. With tension and compression, where - some numerical parameter, and d — a typical cross-section size. In this case from the probabilities of the conversion formula follows that the law of the parameter distribution k has the form

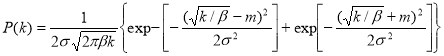
Where m, — mathematical and random value standard d. The first two points of distribution are equal

Where k_d=σ/m — the coefficient of the size variation.

When bending and torsion k=bd³ and transformation of probabilities

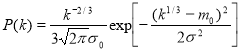
where_o=^1/3, m_o=m^1/3.

The mathematical expectation and variance of the parameter k can be found by performing two successive changes of values

Then

,

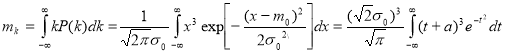
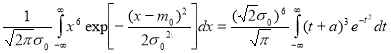Where

Now, taking into account the table integrals we obtain

,

.(5)

The displacement with bend and torsion . Then

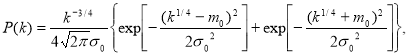
Where , .

We find the first two moments of the distribution. Using the above-mentioned changes of values again, we finally obtain

(6)

The first two points of the k parameter can be found approximately in the case when the distribution of P (k) is unknown. For that the use of the function expansion in a Taylor series, and applying to it the mathematical averaging operation are necessary

Let . Taking the three members of the Taylor series, we get

(7)

In solving engineering problems, there are cases when the laws of random values distribution are unknown, but several their first moment sare known. In this case, the probabilistic-stress characteristics can be determined approximately by the decomposition of (1) in a Taylor series. Thus, it is obtained in [1]

(8)

Where — coefficients of variation.

If the moments of higher order, are known these expressions can be specify, taking more members of the Taylor series expansion. So, if we take the three terms of the series, we’ll get

This approach is justified in the case where the distribution of random variables are known, the integral (4) is not taken analytically.

If the density of the stress distribution is know, the probability of arbitrary level stress exceeding [1] can be found:

.(9)

It is considered in the example, where the load and parameter of k and are subject to the gamma distribution

Then according to the formula (4) we have

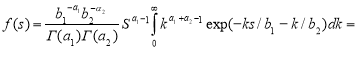
Where

Taking into account that — the complete beta function [2]

Wefinally get

It is easy to show that for this distribution the normalization condition is performed.

If we suppose b2 = b1, then we get the well-known beta-distribution [2]

(10)

The moments of order n distribution are equal

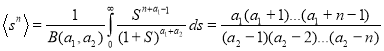
It follows that

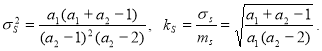(11)

Letsk_q=0,25, k_k=0,2. Then₁= =16, ₂= =25.

Now, using (11) we have

m_s=0,6667, _s=0,22, k_s=0,33.

If we use the approximate formula (8) to determine these characteristics, we obtain

m_s=0,6656, _s=0,205, k_s=0,308.

The difference percent age on the coefficient of variation is 6.6 %.

References:

1. Bakirov Z. B. Probabilistic methods of elements constructions calculation. – Karaganda: KSTU, 2001. 180 p.
2. Handbook of special Functions / Ed. M. Abramowitz and I. Steagan. — M.: Nauka, 1979. 830 p.